人教版数学八年级上册:13.1.2探究线段垂直平分线的性质 课件(20张PPT)
文档属性
| 名称 | 人教版数学八年级上册:13.1.2探究线段垂直平分线的性质 课件(20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览






文档简介
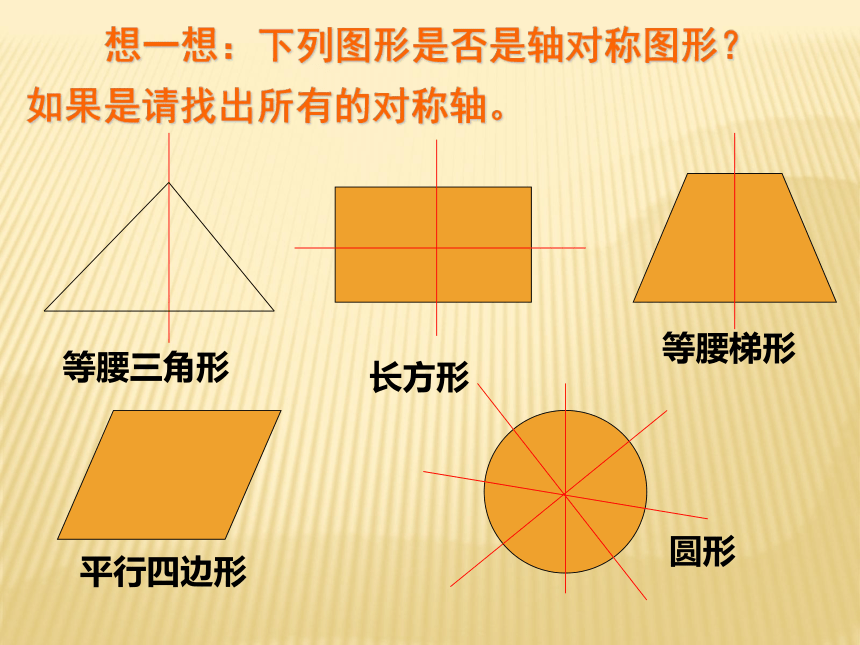
猜字游戏
复习引入
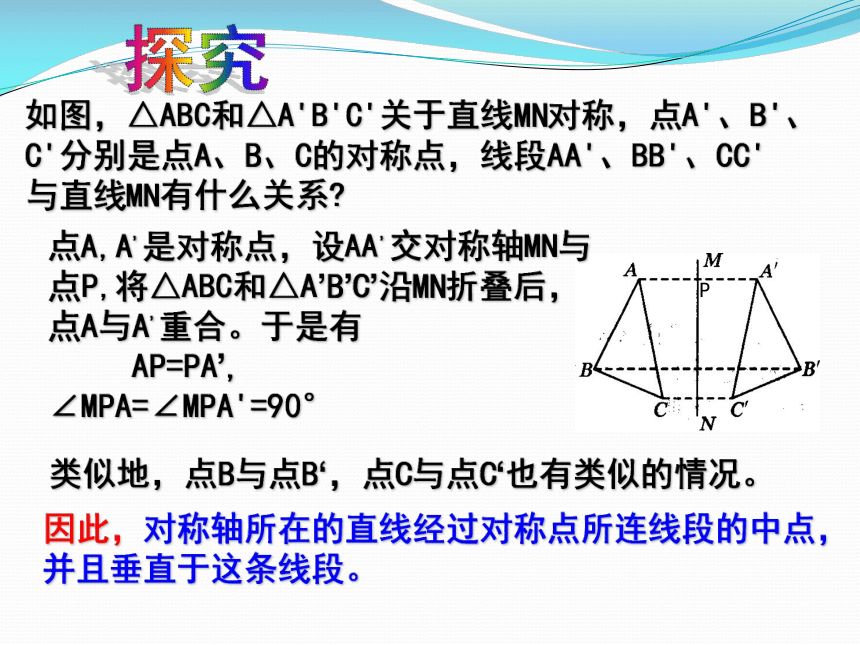
想一想:下列图形是否是轴对称图形?
长方形
等腰梯形
平行四边形
圆形
如果是请找出所有的对称轴。
等腰三角形
P
如图,△ABC和△A'B'C'关于直线MN对称,点A'、B'、C'分别是点A、B、C的对称点,线段AA'、BB'、CC'与直线MN有什么关系?
点A,A,是对称点,设AA,交对称轴MN与
点P,将△ABC和△A’B’C’沿MN折叠后,
点A与A,重合。于是有
AP=PA’,
∠MPA=∠MPA'=90°
类似地,点B与点B‘,点C与点C‘也有类似的情况。
因此,对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
探究
线段的垂直平分线的性质
A
A’
教学目标
1·知识与技能
1.掌握线段的垂直平分线的性质和判定.
2.能灵活运用线段的垂直平分线的性质和判定解题
2·过程与方法:通过经历线段的垂直平分线的性质和判定的证明过程,体验逻辑推理的数学方法
3·情感态度价值观:通过认识上的升华,使学生加深对命题证明的认识
教学目标
重点
难点
【图形轴对称的性质和线段垂直平分线的性质 】
【灵活运用线段的垂直平分线的性质和判定解题】
经过线段中点并且垂直与这条线段的直线,叫做
这条线段的垂直平分线。
这样,我们就得到图形轴对称的性质;
◆如果两个图形关于某条直线对称,哪么对称轴是任何
一对对应点所连线段的垂直平分线。
A
A’
B
B’
C
C’
L
例如右图中,
AA’
BB’
CC’
图4
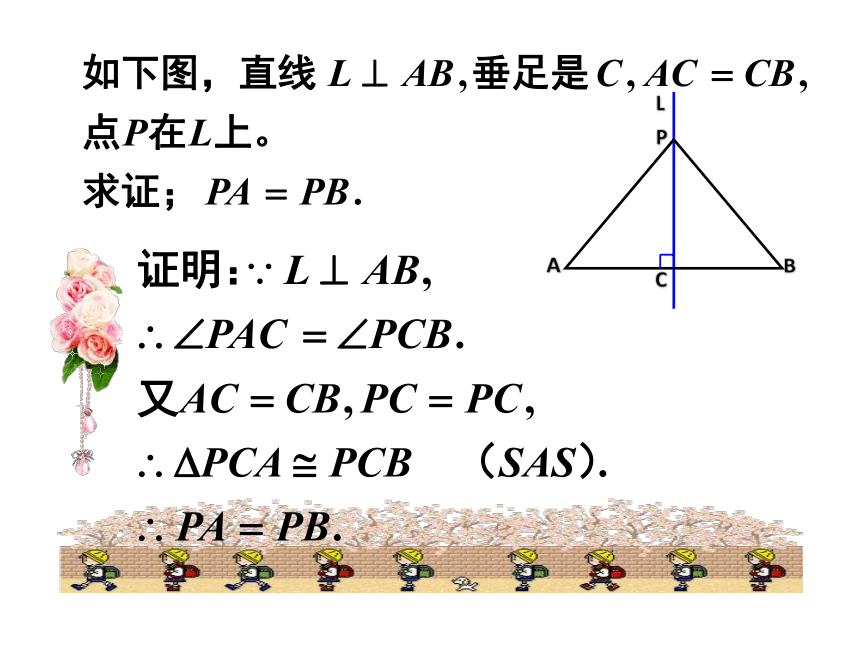
任意画一条线段AB,再画出它的垂直平分线MN,在MN上任意取点P1,P2,P3(如下图),分别量一量点P1,P2,P3到A与B的距离,你有什么发现?你能说明理由吗?请与同伴交流.
我们学过的三角形全等判定方法来很容易
的发现,点P1,P2,P3到点A距离与它们到点B的距离分别相等。
线段垂直平分线上的点与这条
线段两个端点的距离相等。
哪么我们一起利用判定两个三角形全等的方法,证明
这个性质看看哦~
P
A
B
C
L
1 (中考)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
针对性训练
B
2·已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_____________。
针对性训练
13
探索并证明线段垂直平分线的判定
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
探索并证明线段垂直平分线的判定
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上
P
A
B
C
已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.
线段垂直平分线的判定
用几何符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
1 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
(来自《典中点》)
www.xkb1.com
针对性训练
A
3、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
针对性训练
(-3,0)
(-m,0)
课后小结:
1·线段的垂直平分线的概念
2·线段的垂直平分线的性质
3·线段垂直平分线的判定
请 不 要 忘 记 我 哦~
作业:
必做题:大练习册40页,教材书62页 练习
【????????? ????? ???????????????? ?????. 】 ?????????? ??? ????????? ??????? ????????~ ??????????? ?????????? ~ ???????????? ?????...
请 不 要 忘 记 我 哦~
作业:
选做题:如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。
C
????-???!
????????_ %99 ???????????????%1 ????????? ??????.
---???????
再见
复习引入
想一想:下列图形是否是轴对称图形?
长方形
等腰梯形
平行四边形
圆形
如果是请找出所有的对称轴。
等腰三角形
P
如图,△ABC和△A'B'C'关于直线MN对称,点A'、B'、C'分别是点A、B、C的对称点,线段AA'、BB'、CC'与直线MN有什么关系?
点A,A,是对称点,设AA,交对称轴MN与
点P,将△ABC和△A’B’C’沿MN折叠后,
点A与A,重合。于是有
AP=PA’,
∠MPA=∠MPA'=90°
类似地,点B与点B‘,点C与点C‘也有类似的情况。
因此,对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
探究
线段的垂直平分线的性质
A
A’
教学目标
1·知识与技能
1.掌握线段的垂直平分线的性质和判定.
2.能灵活运用线段的垂直平分线的性质和判定解题
2·过程与方法:通过经历线段的垂直平分线的性质和判定的证明过程,体验逻辑推理的数学方法
3·情感态度价值观:通过认识上的升华,使学生加深对命题证明的认识
教学目标
重点
难点
【图形轴对称的性质和线段垂直平分线的性质 】
【灵活运用线段的垂直平分线的性质和判定解题】
经过线段中点并且垂直与这条线段的直线,叫做
这条线段的垂直平分线。
这样,我们就得到图形轴对称的性质;
◆如果两个图形关于某条直线对称,哪么对称轴是任何
一对对应点所连线段的垂直平分线。
A
A’
B
B’
C
C’
L
例如右图中,
AA’
BB’
CC’
图4
任意画一条线段AB,再画出它的垂直平分线MN,在MN上任意取点P1,P2,P3(如下图),分别量一量点P1,P2,P3到A与B的距离,你有什么发现?你能说明理由吗?请与同伴交流.
我们学过的三角形全等判定方法来很容易
的发现,点P1,P2,P3到点A距离与它们到点B的距离分别相等。
线段垂直平分线上的点与这条
线段两个端点的距离相等。
哪么我们一起利用判定两个三角形全等的方法,证明
这个性质看看哦~
P
A
B
C
L
1 (中考)如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6 B.5 C.4 D.3
针对性训练
B
2·已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_____________。
针对性训练
13
探索并证明线段垂直平分线的判定
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
探索并证明线段垂直平分线的判定
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上
P
A
B
C
已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.
线段垂直平分线的判定
用几何符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
1 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
(来自《典中点》)
www.xkb1.com
针对性训练
A
3、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是___________。
针对性训练
(-3,0)
(-m,0)
课后小结:
1·线段的垂直平分线的概念
2·线段的垂直平分线的性质
3·线段垂直平分线的判定
请 不 要 忘 记 我 哦~
作业:
必做题:大练习册40页,教材书62页 练习
【????????? ????? ???????????????? ?????. 】 ?????????? ??? ????????? ??????? ????????~ ??????????? ?????????? ~ ???????????? ?????...
请 不 要 忘 记 我 哦~
作业:
选做题:如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。
C
????-???!
????????_ %99 ???????????????%1 ????????? ??????.
---???????
再见
