人教版数学九年级上册 23.2中心对称课件(23张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.2中心对称课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 778.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 12:42:30 | ||
图片预览






文档简介
回顾:
根据我们之前学了旋转知识,请填空
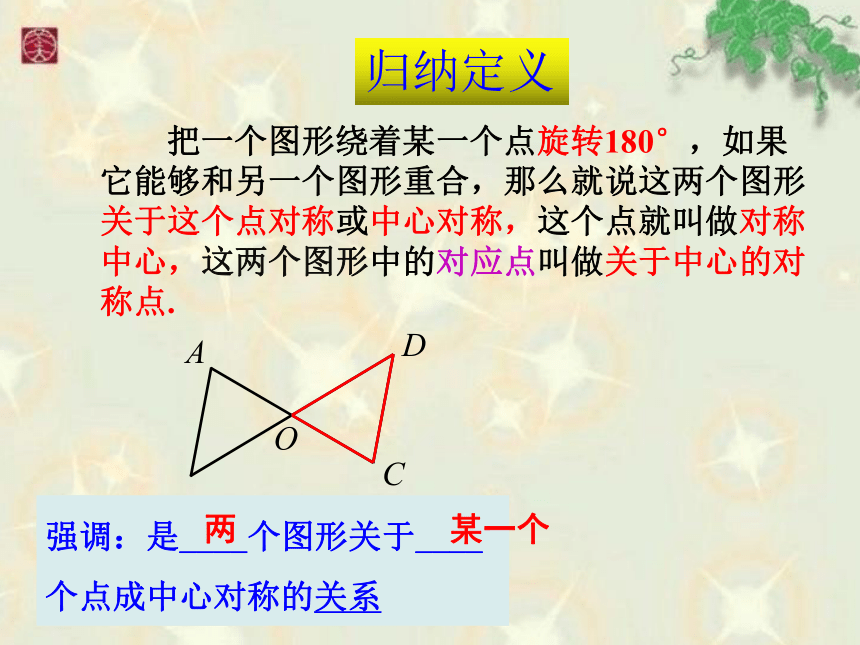
如图,△EDC可以看做由_______旋转得来,其中∠B=∠ACB=50°,则旋转中心是________,旋转角是______________,旋转角等于_________,
AB=_______=_______=________
BC=_________
△ABC
点C
∠BCE或∠ACD
50°
AC
CD
DE
CE
中心对称
和中心对称图形
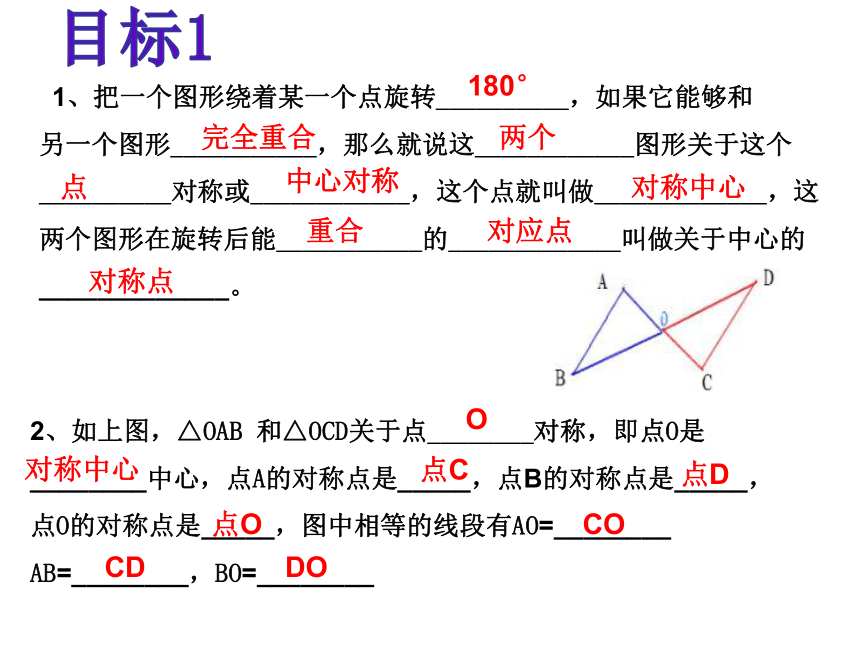
把一个图形绕着某一个点旋转180°,如果它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
归纳定义
强调:是____个图形关于____
个点成中心对称的关系
两
某一个
A
D
C
O
完成学案的
目标 1
1、把一个图形绕着某一个点旋转__________,如果它能够和
另一个图形___________,那么就说这____________图形关于这个__________对称或____________,这个点就叫做_____________,这两个图形在旋转后能___________的_____________叫做关于中心的_____________。
2、如上图,△OAB 和△OCD关于点________对称,即点O是
________中心,点A的对称点是_____,点B的对称点是_____,
点O的对称点是_____,图中相等的线段有AO=________
AB=________,BO=________
目标1
180°
完全重合
两个
点
中心对称
对称中心
重合
对应点
对称点
O
对称中心
点C
点D
点O
CO
CD
DO
探究中心对称的性质
问题:中心对称是特殊的旋转,
它有哪些性质?
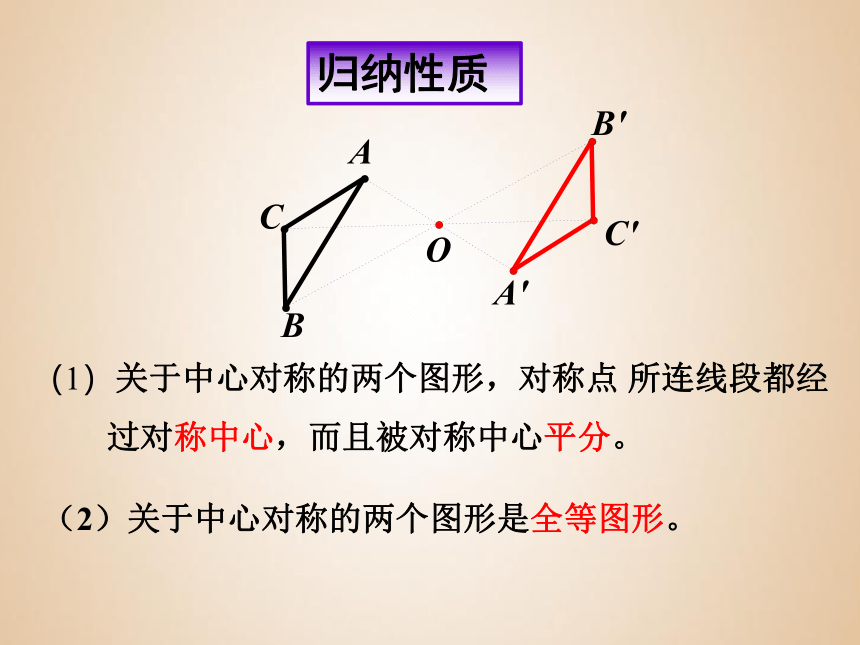
(1)关于中心对称的两个图形,对称点 所连线段都经
过对称中心,而且被对称中心平分。
归纳性质
(2)关于中心对称的两个图形是全等图形。
完成学案的
目标 2
3、关于中心对称的两个图形,对应线段的关系是( )
A、平行 B、相等 C、平行且相等
D、相等且平行或在同一直线上
2、下列说法不正确的是( )
A、关于中心对称的两个图形的对应点到对称中心的距离相等
B、关于中心对称的两个图形的对应点和对称中心三点在同一直线上
C、关于中心对称的两个图形全等
D、两个图形全等一定构成中心对称
D
D
1、如右图,∵△ABC与△A’B’C’关于点O成中心对称,
∴AO=______,BO=______,CO______
∵△ABC __________
A'O
B'O
C'O
△A'B'C'
目标2
中心对称作图
那么,我们是如何作出一个图形
关于某一个点的中心对称图形的呢?一起来看看
A’
C’
B’
完成学案的
目标 3
A′
B′
C ′
O
A
B
C
1 、如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
特殊:对称中心在图形内
2、画一个与已知四边形ABCD成中心对称的图形.
以顶点A为对称中心
D
A
B
C
E
F
G
特殊:对称中心在图形的顶点
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
观 察
跟原来图形__________
重合
A
B
C
D
O
定义:
把一个图形绕着某一个点旋转______,如果旋转后图像能够与___________重合,那么这个图形叫_____________,这个点叫__________
180°
原来的图形
中心对称图形
对称中心
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系,
中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,
则它们成中心对称.
比 较
问题:我们平时见过的几何图形中,有哪些是中心对称图形?
牛刀小试
√
√
√
√
√
√
√
√
完成学案的
目标 4
中心对称 与 中心对称图形 的区别
1、中心对称 —— 指两个图形经过180°旋转成中心对称的关系(强调是一种关系)
2、中心对称图形 ——指一个图形经过180°旋转与自己重合(强调一个图形的性质)
小结:
1.如图,在一次游戏当中,小明将下面第一排的四张扑克牌中的一张旋转180?后,得到第二排,看完后,你能很快知道小明转动了哪一张扑克吗?
作业
在生活中你还见过哪些中心对称图形?
回
H
√
√
√
√
√
√
√
中心对称图形
轴对称图形
既是中心对称图形又是轴对称图形
回
H
填一填
① ② ③
④ ⑤ ⑥
⑦ ⑧ ⑨
① ② ③ ④
⑤ ⑧ ⑨
① ② ③ ④
⑤ ⑥ ⑧ ⑨
① ② ③ ④
⑤ ⑧ ⑨
完成南方新课堂
P50—53
根据我们之前学了旋转知识,请填空
如图,△EDC可以看做由_______旋转得来,其中∠B=∠ACB=50°,则旋转中心是________,旋转角是______________,旋转角等于_________,
AB=_______=_______=________
BC=_________
△ABC
点C
∠BCE或∠ACD
50°
AC
CD
DE
CE
中心对称
和中心对称图形
把一个图形绕着某一个点旋转180°,如果它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
归纳定义
强调:是____个图形关于____
个点成中心对称的关系
两
某一个
A
D
C
O
完成学案的
目标 1
1、把一个图形绕着某一个点旋转__________,如果它能够和
另一个图形___________,那么就说这____________图形关于这个__________对称或____________,这个点就叫做_____________,这两个图形在旋转后能___________的_____________叫做关于中心的_____________。
2、如上图,△OAB 和△OCD关于点________对称,即点O是
________中心,点A的对称点是_____,点B的对称点是_____,
点O的对称点是_____,图中相等的线段有AO=________
AB=________,BO=________
目标1
180°
完全重合
两个
点
中心对称
对称中心
重合
对应点
对称点
O
对称中心
点C
点D
点O
CO
CD
DO
探究中心对称的性质
问题:中心对称是特殊的旋转,
它有哪些性质?
(1)关于中心对称的两个图形,对称点 所连线段都经
过对称中心,而且被对称中心平分。
归纳性质
(2)关于中心对称的两个图形是全等图形。
完成学案的
目标 2
3、关于中心对称的两个图形,对应线段的关系是( )
A、平行 B、相等 C、平行且相等
D、相等且平行或在同一直线上
2、下列说法不正确的是( )
A、关于中心对称的两个图形的对应点到对称中心的距离相等
B、关于中心对称的两个图形的对应点和对称中心三点在同一直线上
C、关于中心对称的两个图形全等
D、两个图形全等一定构成中心对称
D
D
1、如右图,∵△ABC与△A’B’C’关于点O成中心对称,
∴AO=______,BO=______,CO______
∵△ABC __________
A'O
B'O
C'O
△A'B'C'
目标2
中心对称作图
那么,我们是如何作出一个图形
关于某一个点的中心对称图形的呢?一起来看看
A’
C’
B’
完成学案的
目标 3
A′
B′
C ′
O
A
B
C
1 、如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.
特殊:对称中心在图形内
2、画一个与已知四边形ABCD成中心对称的图形.
以顶点A为对称中心
D
A
B
C
E
F
G
特殊:对称中心在图形的顶点
o
(2)圆
(4) 正方形
(1)线段
(3)平行四边形
A
B
将下面的图形绕O点旋转180°,你有什么发现?
O
O
O
观 察
跟原来图形__________
重合
A
B
C
D
O
定义:
把一个图形绕着某一个点旋转______,如果旋转后图像能够与___________重合,那么这个图形叫_____________,这个点叫__________
180°
原来的图形
中心对称图形
对称中心
中心对称与中心对称图形是两个既有联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系,
中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体,
则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,
则它们成中心对称.
比 较
问题:我们平时见过的几何图形中,有哪些是中心对称图形?
牛刀小试
√
√
√
√
√
√
√
√
完成学案的
目标 4
中心对称 与 中心对称图形 的区别
1、中心对称 —— 指两个图形经过180°旋转成中心对称的关系(强调是一种关系)
2、中心对称图形 ——指一个图形经过180°旋转与自己重合(强调一个图形的性质)
小结:
1.如图,在一次游戏当中,小明将下面第一排的四张扑克牌中的一张旋转180?后,得到第二排,看完后,你能很快知道小明转动了哪一张扑克吗?
作业
在生活中你还见过哪些中心对称图形?
回
H
√
√
√
√
√
√
√
中心对称图形
轴对称图形
既是中心对称图形又是轴对称图形
回
H
填一填
① ② ③
④ ⑤ ⑥
⑦ ⑧ ⑨
① ② ③ ④
⑤ ⑧ ⑨
① ② ③ ④
⑤ ⑥ ⑧ ⑨
① ② ③ ④
⑤ ⑧ ⑨
完成南方新课堂
P50—53
同课章节目录
