人教版数学九年级上册24.1. 3弧、弦、圆心角课件(18张)
文档属性
| 名称 | 人教版数学九年级上册24.1. 3弧、弦、圆心角课件(18张) |  | |
| 格式 | ppt | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 11:57:08 | ||
图片预览




文档简介
义务教育课程标准实验教科书
九年级 上册
人民教育出版社
24.1.3弧、弦、圆心角
回顾
什么叫等弧?
在同圆或等圆中,能够互相重合的弧叫等弧·
垂径定理的内容什么?
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
圆是中心对称图形吗?它的对称中心在哪里?
·
一、思考
圆是中心对称图形,
它的对称中心是圆心.
这就是圆的旋转不变性
实际上把圆绕圆心旋转任意角度后,所得图形都与原图重合.
·
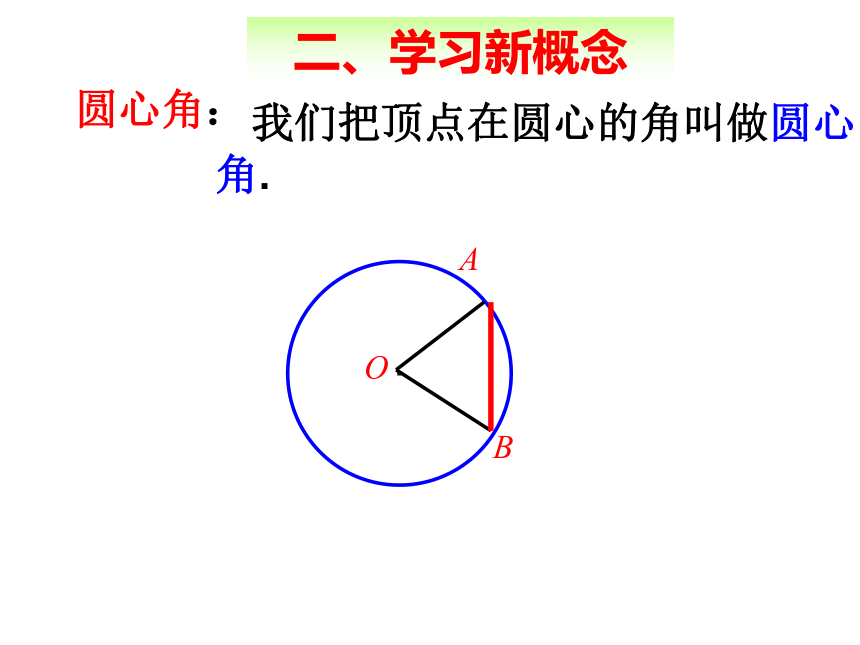
圆心角:
O
B
A
二、学习新概念
我们把顶点在圆心的角叫做圆心角.
小试牛刀
下面各图中的角是不是圆心角?
×
√
√
×
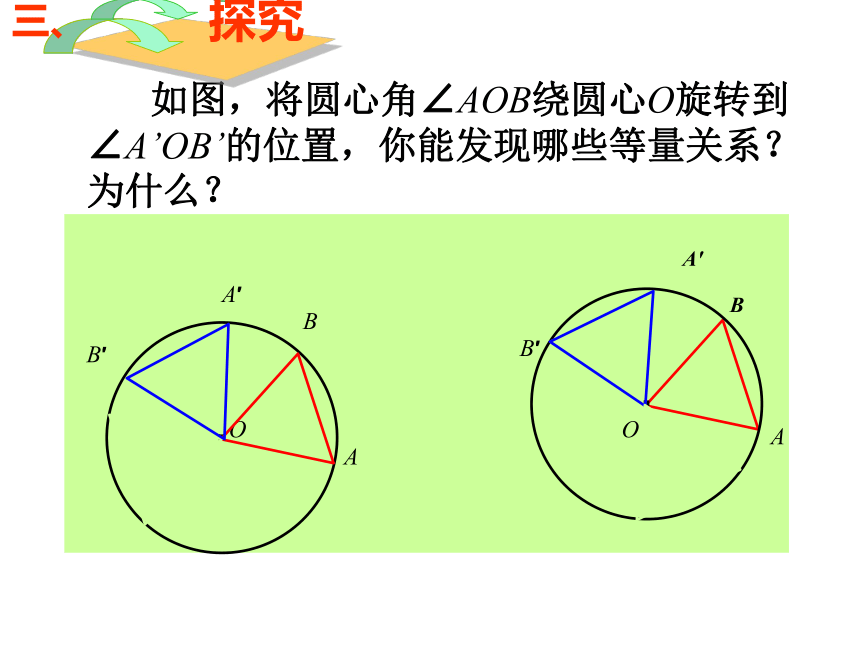
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
·
O
A
B
探究
O
·
A
B
A′
B′
A′
B′
三、
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧和劣弧分别______.
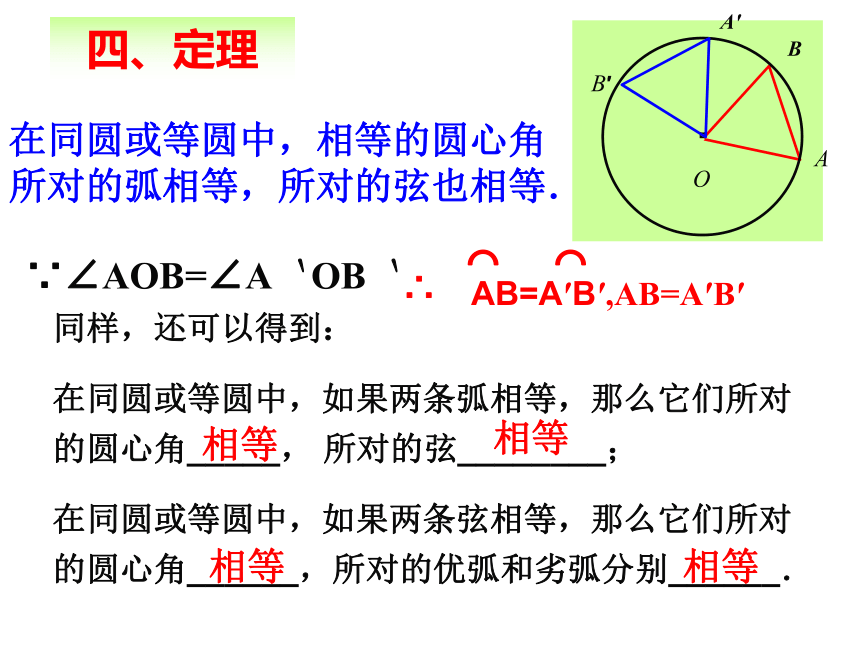
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
四、定理
·
O
A
B
A′
B′
∵∠AOB=∠A`OB`
⌒ ⌒
AB=A′B′,AB=A′B′
∴
·
O
A
B
A′
B′
圆心角定理及推广定理:
在同圆或等圆中,两个圆心角、两条弧、
两条弦中如果有一组量相等,那么它们所
对应的其余各组量也相等。
即:在同圆或等圆中
⌒ ⌒
AB=A′B′
∠AOB=∠A′OB′
知
1
推
2
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,______________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果AB=CD,
OE⊥AB于E,
OF⊥CD于F,
OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
五、定理巩固练习
⌒ ⌒
AB = CD
⌒ ⌒
AB = CD
⌒ ⌒
AB = CD
∵ OE⊥AB,OF ⊥CD
理由如下:
相等.
A
B
C
D
E
F
O
∵ AB=CD,
∴ AE=CF,
∵ OA=OC,
∴△ AOE≌△COF(HL)
∴OE=OF
·
A
B
C
O
六、例题
例1 如图在⊙O中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
⌒ ⌒
AB = AC
证明:
⌒ ⌒
AB = AC
∵
∴AB=AC,△ABC是等腰三角形
又∵∠ACB=60°,
∴△ABC是等边三角形
∴AB=BC=CA
∴∠AOB=∠BOC=∠AOC
如图,AB是⊙O的直径, ∠COD=35°,求∠AOE的度数.
·
A
O
B
C
D
E
练习1
⌒ ⌒ ⌒
BC=CD=DE
·
A
O
B
C
D
E
∴ ∠BOC=∠COD=∠DOE =35°
∴ ∠AOE=180°-3×35°=75°
CD
BC
DE
= =
∵
解:
如图,已知
求证:AB=CD
. O
A
B
C
D
变式:如图,如果AD=BC,求证:AB=CD
练习2
⌒ ⌒
AD=BC
能力提高
如图,在⊙O中,已知
求证:CD=CE
⌒ ⌒
AC=BC,D、E分别
是半径OA、OB的中点,
证明:
连接OC,
⌒ ⌒
∵ AC=BC,
∴∠AOC=∠BOC
∵D、E分别是半径OA、OB的中点,
∴△ COD≌△COE
(1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?
七.课堂小结
《全程突破》P74
八.布置作业
谢谢指导!
九年级 上册
人民教育出版社
24.1.3弧、弦、圆心角
回顾
什么叫等弧?
在同圆或等圆中,能够互相重合的弧叫等弧·
垂径定理的内容什么?
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
圆是中心对称图形吗?它的对称中心在哪里?
·
一、思考
圆是中心对称图形,
它的对称中心是圆心.
这就是圆的旋转不变性
实际上把圆绕圆心旋转任意角度后,所得图形都与原图重合.
·
圆心角:
O
B
A
二、学习新概念
我们把顶点在圆心的角叫做圆心角.
小试牛刀
下面各图中的角是不是圆心角?
×
√
√
×
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
·
O
A
B
探究
O
·
A
B
A′
B′
A′
B′
三、
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____, 所对的弦________;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧和劣弧分别______.
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
四、定理
·
O
A
B
A′
B′
∵∠AOB=∠A`OB`
⌒ ⌒
AB=A′B′,AB=A′B′
∴
·
O
A
B
A′
B′
圆心角定理及推广定理:
在同圆或等圆中,两个圆心角、两条弧、
两条弦中如果有一组量相等,那么它们所
对应的其余各组量也相等。
即:在同圆或等圆中
⌒ ⌒
AB=A′B′
∠AOB=∠A′OB′
知
1
推
2
1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,______________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果AB=CD,
OE⊥AB于E,
OF⊥CD于F,
OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
五、定理巩固练习
⌒ ⌒
AB = CD
⌒ ⌒
AB = CD
⌒ ⌒
AB = CD
∵ OE⊥AB,OF ⊥CD
理由如下:
相等.
A
B
C
D
E
F
O
∵ AB=CD,
∴ AE=CF,
∵ OA=OC,
∴△ AOE≌△COF(HL)
∴OE=OF
·
A
B
C
O
六、例题
例1 如图在⊙O中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
⌒ ⌒
AB = AC
证明:
⌒ ⌒
AB = AC
∵
∴AB=AC,△ABC是等腰三角形
又∵∠ACB=60°,
∴△ABC是等边三角形
∴AB=BC=CA
∴∠AOB=∠BOC=∠AOC
如图,AB是⊙O的直径, ∠COD=35°,求∠AOE的度数.
·
A
O
B
C
D
E
练习1
⌒ ⌒ ⌒
BC=CD=DE
·
A
O
B
C
D
E
∴ ∠BOC=∠COD=∠DOE =35°
∴ ∠AOE=180°-3×35°=75°
CD
BC
DE
= =
∵
解:
如图,已知
求证:AB=CD
. O
A
B
C
D
变式:如图,如果AD=BC,求证:AB=CD
练习2
⌒ ⌒
AD=BC
能力提高
如图,在⊙O中,已知
求证:CD=CE
⌒ ⌒
AC=BC,D、E分别
是半径OA、OB的中点,
证明:
连接OC,
⌒ ⌒
∵ AC=BC,
∴∠AOC=∠BOC
∵D、E分别是半径OA、OB的中点,
∴△ COD≌△COE
(1)本节课学习了哪些内容?
(2)圆心角、弧、弦之间有哪些关系?
七.课堂小结
《全程突破》P74
八.布置作业
谢谢指导!
同课章节目录
