人教版数学九年级上册24.1.3弧、弦、圆心角课件(32张)
文档属性
| 名称 | 人教版数学九年级上册24.1.3弧、弦、圆心角课件(32张) |  | |
| 格式 | ppt | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 08:08:52 | ||
图片预览



文档简介
24.1.3 圆心角
O
C
D
A
B
E
2、由圆的轴对称性得到:
1、圆是 图形,
轴对称
直径所在的直线
每一条 都是它的对称轴。
垂径定理及逆定理
温故知新
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
B
A
圆绕圆心旋转
?
探究新知:
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
B
A
180°
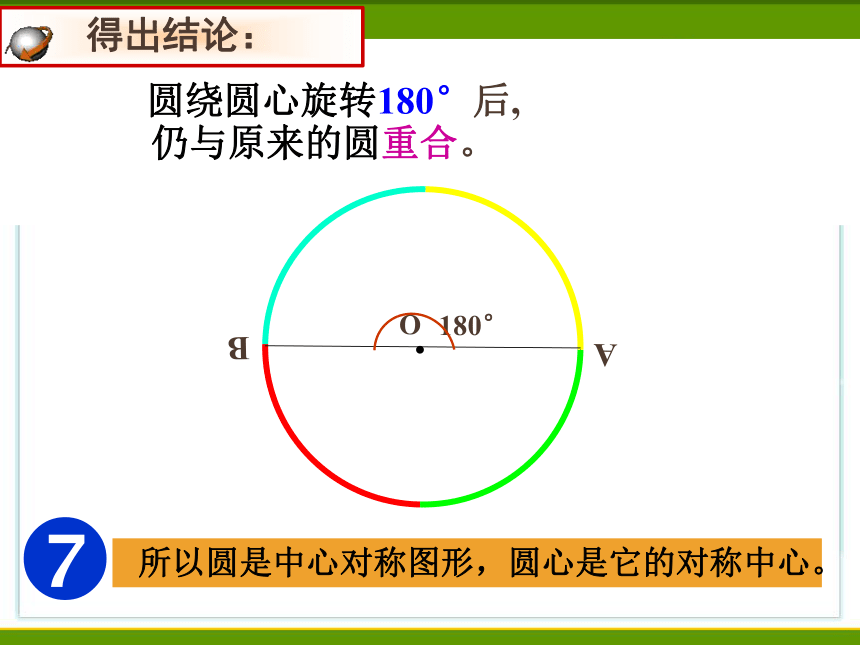
所以圆是中心对称图形,圆心是它的对称中心。
圆绕圆心旋转180°后,
?
仍与原来的圆重合。
得出结论:
N
O
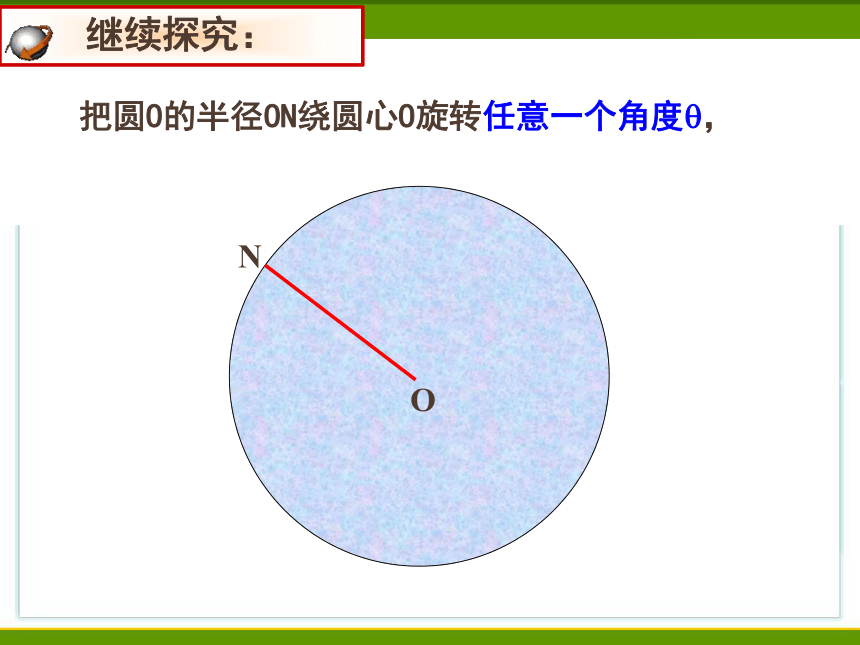
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
N
O
N'
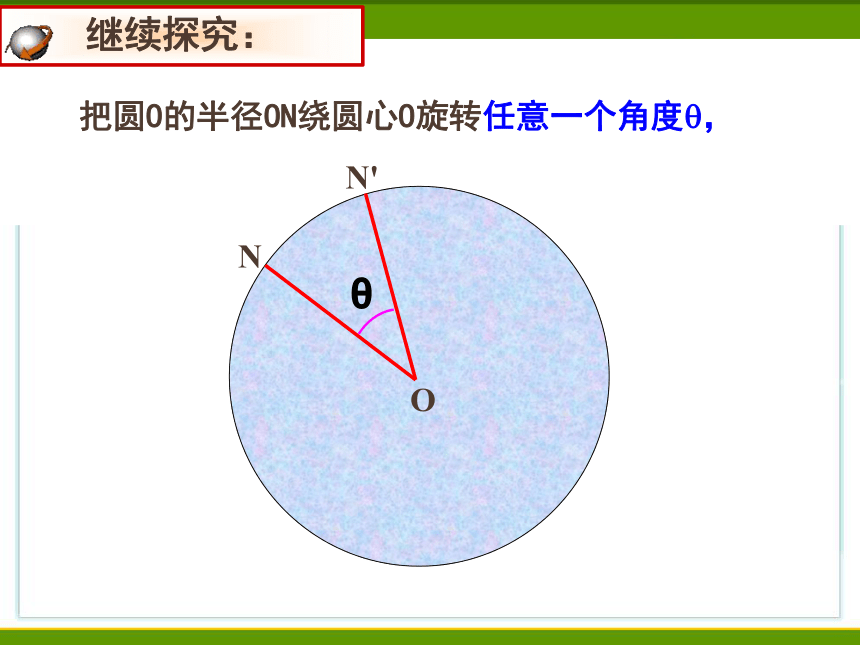
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
θ
N
O
N'
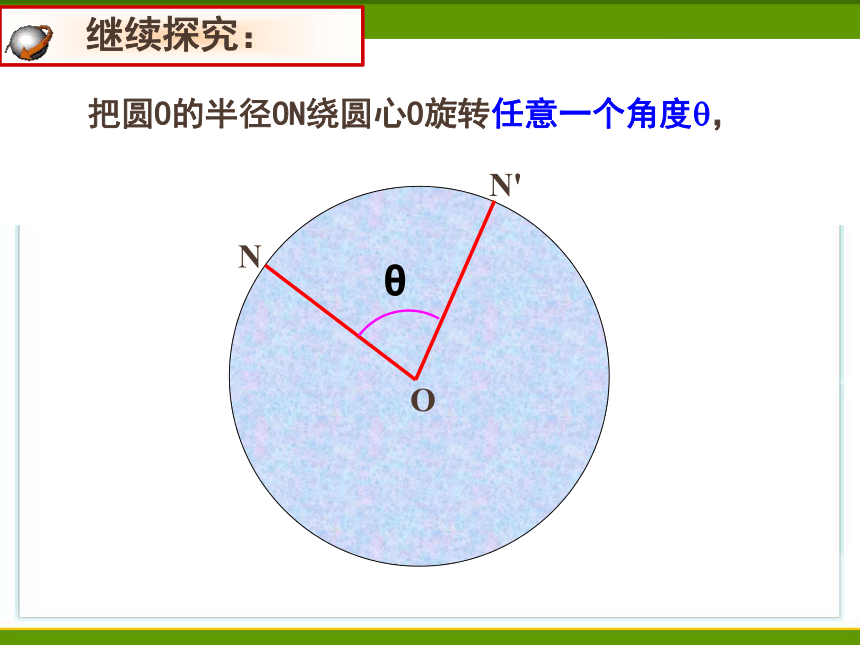
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
θ
N
O
N'
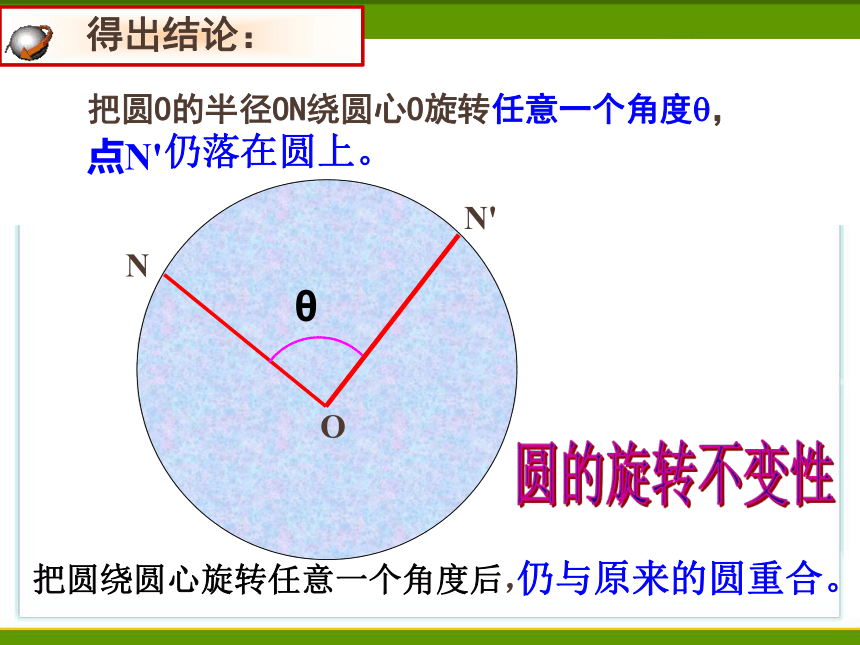
把圆绕圆心旋转任意一个角度后,
把圆O的半径ON绕圆心O旋转任意一个角度?,
点N'
圆的旋转不变性
仍与原来的圆重合。
仍落在圆上。
得出结论:
θ
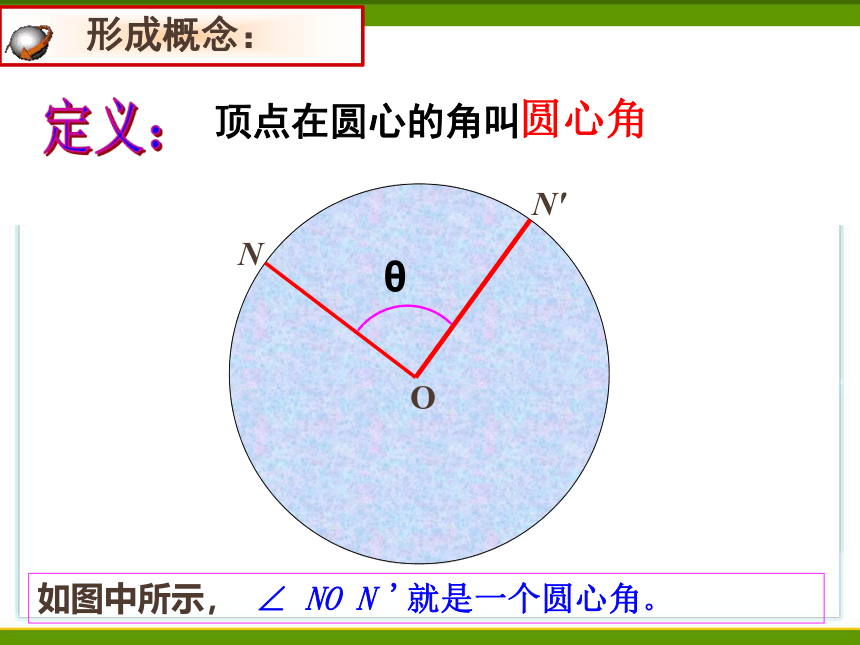
如图中所示, ∠ NO N '就是一个圆心角。
N
O
N'
定义:
形成概念:
顶点在圆心的角叫
圆心角
θ
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
顶点在圆心的角叫圆心角。
及时反馈:
C
D
o
A
B
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件:
∠ AOB= ∠ COD
C
D
o
A
B
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件: AOB= COD
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件: AOB= COD
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
∵OA=OC ,OB=OD
∠AOB=∠COD,
∴把 ∠COD连同 CD、 弦CD 绕圆心O 旋转, 当点A与点C重合时,
点B与点D也重合。
∴
AB= CD,
⌒
⌒
AB=CD
A
B
C
D
o
弦AB和弦CD对应的弦心距什么关系?
在同圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD AB=CD
想一想:
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
几何表述:
OE=OF
形成定理:
圆心角定理
A
B
C
D
o
圆心角定理:
在同圆或等圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
几何表述:
OE=OF
AB=CD
在同圆或等圆中,
相等的圆心角所对的弧相等,所对的弦也相等。
【注意】:
1.去掉“在同圆或等圆中”结论不一定成立。
2 .要证弧(弦)相等,只需证它们所对的圆心角相等。
分析定理:
圆心角定理
A
B
C
D
o
应用新知:
O
A
B
C
D
1
2
例 已知:如图,∠1=∠2.求证:AC=BD.
【变式】 已知:如图,∠1=∠2.
求证:AC=BD.
圆心角定理
圆心角相等
所对弧相等
所对弦相等
所对弦的弦心距相等
证明:∵ ∠ 1= ∠ 2
∴DC=BA( )
∴ DC+BC= BA+BC
即 BD=AC
反思:
圆心角定理
课堂小结:
1、圆是中心对称图形,圆具有旋转不变性;
2、圆心角定理:
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
通过本节的学习,你对圆有哪些新的认识?
多谢指导!
O
C
D
A
B
E
2、由圆的轴对称性得到:
1、圆是 图形,
轴对称
直径所在的直线
每一条 都是它的对称轴。
垂径定理及逆定理
温故知新
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
B
A
圆绕圆心旋转
?
探究新知:
.
O
A
B
圆绕圆心旋转
?
探究新知:
.
O
B
A
180°
所以圆是中心对称图形,圆心是它的对称中心。
圆绕圆心旋转180°后,
?
仍与原来的圆重合。
得出结论:
N
O
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
N
O
N'
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
θ
N
O
N'
把圆O的半径ON绕圆心O旋转任意一个角度?,
继续探究:
θ
N
O
N'
把圆绕圆心旋转任意一个角度后,
把圆O的半径ON绕圆心O旋转任意一个角度?,
点N'
圆的旋转不变性
仍与原来的圆重合。
仍落在圆上。
得出结论:
θ
如图中所示, ∠ NO N '就是一个圆心角。
N
O
N'
定义:
形成概念:
顶点在圆心的角叫
圆心角
θ
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
顶点在圆心的角叫圆心角。
及时反馈:
C
D
o
A
B
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件:
∠ AOB= ∠ COD
C
D
o
A
B
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件: AOB= COD
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件: AOB= COD
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
条件: AOB= COD
o
A
B
C
D
探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD,
⌒
⌒
AB=CD
猜想:
证明:
∵OA=OC ,OB=OD
∠AOB=∠COD,
∴把 ∠COD连同 CD、 弦CD 绕圆心O 旋转, 当点A与点C重合时,
点B与点D也重合。
∴
AB= CD,
⌒
⌒
AB=CD
A
B
C
D
o
弦AB和弦CD对应的弦心距什么关系?
在同圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD AB=CD
想一想:
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
几何表述:
OE=OF
形成定理:
圆心角定理
A
B
C
D
o
圆心角定理:
在同圆或等圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
几何表述:
OE=OF
AB=CD
在同圆或等圆中,
相等的圆心角所对的弧相等,所对的弦也相等。
【注意】:
1.去掉“在同圆或等圆中”结论不一定成立。
2 .要证弧(弦)相等,只需证它们所对的圆心角相等。
分析定理:
圆心角定理
A
B
C
D
o
应用新知:
O
A
B
C
D
1
2
例 已知:如图,∠1=∠2.求证:AC=BD.
【变式】 已知:如图,∠1=∠2.
求证:AC=BD.
圆心角定理
圆心角相等
所对弧相等
所对弦相等
所对弦的弦心距相等
证明:∵ ∠ 1= ∠ 2
∴DC=BA( )
∴ DC+BC= BA+BC
即 BD=AC
反思:
圆心角定理
课堂小结:
1、圆是中心对称图形,圆具有旋转不变性;
2、圆心角定理:
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等,
所对弦的弦心距相等.
通过本节的学习,你对圆有哪些新的认识?
多谢指导!
同课章节目录
