人教版 八年级数学上册 13.4 课题学习 最短路径 同步培优(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 13.4 课题学习 最短路径 同步培优(Word版 含答案) |

|
|
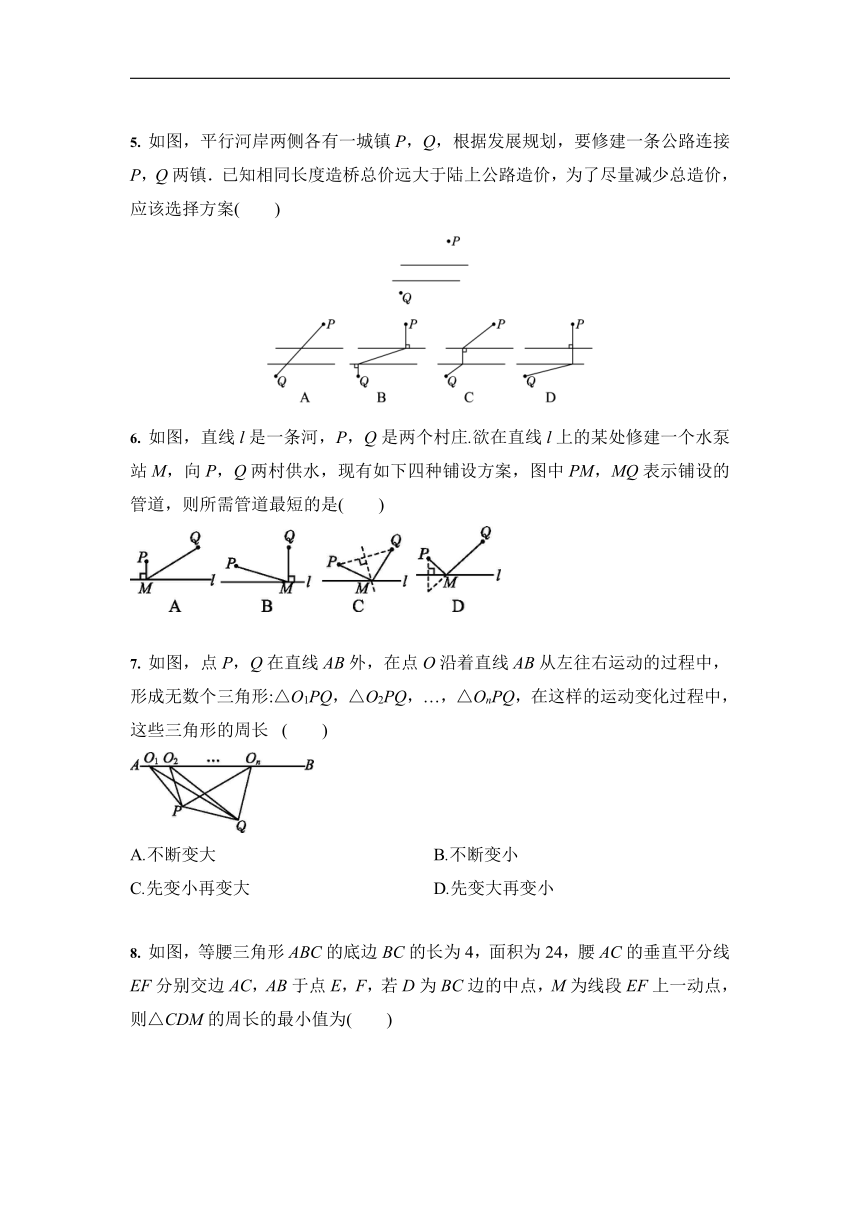
| 格式 | doc | ||
| 文件大小 | 629.2KB | ||
| 资源类型 | 教案 | ||
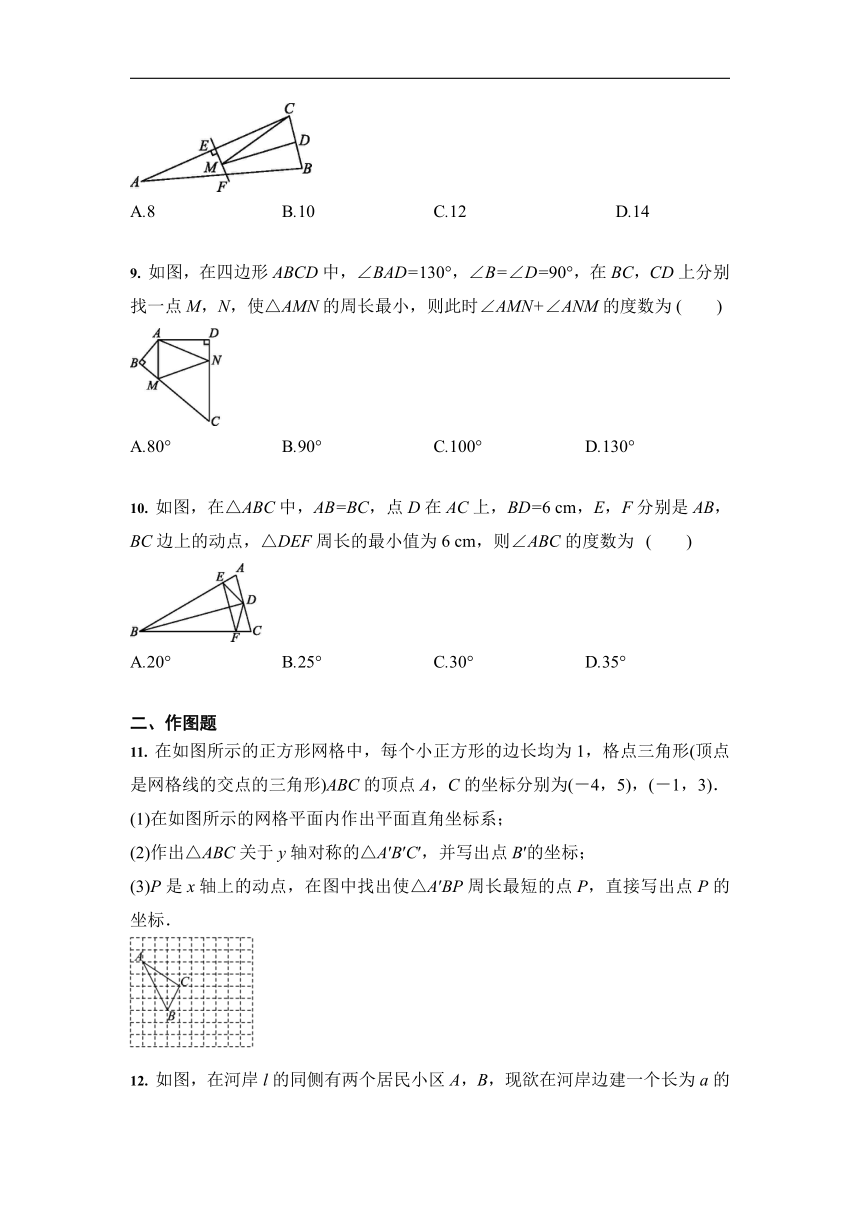
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览



文档简介
人教版 八年级数学上册 13.4 课题学习 最短路径 同步培优
一、选择题
1. 如图,A,B是两个居民小区,快递公司准备在公路l上的点P处建一个服务中心,使PA+PB最短.下面四种选址方案符合要求的是( )
2. 如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为( )
A.10 B.11 C.11.5 D.13
3. 如图,在四边形ABCD中,AB∥CD,AD⊥AB,P是AD边上的一动点,要使PC+PB的值最小,则点P应满足( )
A.PB=PC B.PA=PD
C.∠BPC=90° D.∠APB=∠DPC
4. 如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
5. 如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
6. 如图,直线l是一条河,P,Q是两个村庄.欲在直线l上的某处修建一个水泵站M,向P,Q两村供水,现有如下四种铺设方案,图中PM,MQ表示铺设的管道,则所需管道最短的是( )
7. 如图,点P,Q在直线AB外,在点O沿着直线AB从左往右运动的过程中,形成无数个三角形:△O1PQ,△O2PQ,…,△OnPQ,在这样的运动变化过程中,这些三角形的周长 ( )
A.不断变大 B.不断变小
C.先变小再变大 D.先变大再变小
8. 如图,等腰三角形ABC的底边BC的长为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为( )
A.8 B.10 C.12 D.14
9. 如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则此时∠AMN+∠ANM的度数为 ( )
A.80° B.90° C.100° D.130°
10. 如图,在△ABC中,AB=BC,点D在AC上,BD=6 cm,E,F分别是AB,BC边上的动点,△DEF周长的最小值为6 cm,则∠ABC的度数为 ( )
A.20° B.25° C.30° D.35°
二、作图题
11. 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短的点P,直接写出点P的坐标.
12. 如图,在河岸l的同侧有两个居民小区A,B,现欲在河岸边建一个长为a的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图中画出绿化带的位置,并写出画图过程.
13. 河岸l同侧的两个居民小区A,B到河岸的距离分别为a米,b米(即图①中所示,AA′=a米,BB′=b米),A′B′=c米.现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.
在图②中画出绿化带的位置,并写出画图过程.
14. 如图,山娃星期天从A处赶了几只羊到草地l1放羊,然后赶羊到小河l2饮水,之后再回到B处的家,假设山娃赶羊走的都是直路,请你为他设计一条最短的路线,标明放羊与饮水的位置.
15. 如图,已知牧马营地在点M处,每天牧马人要赶着马群到河边饮水.
(1)求到河边饮水的最短路线;
(2)如果饮完水后,需再到草地吃草,然后回到营地,试设计出最短的牧马路线.
三、解答题
16. 如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图①,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图②,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并求出这个最小值.
17. 如图①所示,A,B两地在一条河的两岸,现要在河岸上造一座桥MN,桥造在何处才能使从A地到B地的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
[思考1]如图②,如果A,B两地之间有两条平行的河流,我们要建的桥都是与河岸垂直的,我们应该如何找到这个最短的路径呢?
[思考2]如图③,如果A,B两地之间有三条平行的河流呢?
[拓展]如图④,如果在上述其他条件不变的情况下,两条河并不是平行的,又该如何建桥呢?
请将你的思考在下面准备好的图形中表示出来,保留作图痕迹,将行走的路线用实线画出来.
人教版 八年级数学上册 13.4 课题学习 最短路径 同步培优-答案
一、选择题
1. 【答案】A
2. 【答案】A [解析] ∵直线m垂直平分AB,∴B,C关于直线m对称.设直线m交AB于点D,∴当点P和点D重合时,AP+CP的值最小,最小值等于AB的长,∴△APC的周长的最小值是6+4=10.
3. 【答案】D
4. 【答案】B [解析] 如图,分别作点A关于BC,DC的对称点A1,A2,连接A1A2交BC于点M,交DC于点N,则此时△AMN的周长最小.∵∠A1AA2=120°,∴∠A1+∠A2=60°.∵MA=MA1,NA=NA2,∴∠AMN+∠ANM=2(∠A1+∠A2)=2×60°=120°.
5. 【答案】C [解析] 如图,作PP′垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于点N,将P′N沿竖直方向向上平移河宽个单位长度,得到PM,PM-MN-NQ即所求.根据“两点之间,线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
6. 【答案】D
7. 【答案】C [解析] 如图,作点P关于直线AB的对称点P',连接P'Q交直线AB于点O.
∵两点之间线段最短,且PQ的长为定值,
∴当点O运动到此点时三角形的周长最短.
∴这些三角形的周长先变小再变大.
8. 【答案】D [解析] 如图,连接AD,MA.
∵△ABC是等腰三角形,D是底边BC的中点,
∴AD⊥BC.
∴S△ABC=BC·AD=×4AD=24,
解得AD=12.
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC.
∴MC+DM=MA+DM≥AD.
∴AD的长为MC+MD的最小值.
∴△CDM的周长的最小值为(MC+MD)+CD=AD+BC=12+×4=14.故选D.
9. 【答案】C [解析] 如图,延长AB到点A',使得BA'=BA,延长AD到点A″,使得DA″=AD,连接A'A″与BC,CD分别交于点M,N.
∵∠ABC=∠ADC=90°,
∴点A,A'关于BC对称,点A,A″关于CD对称,此时△AMN的周长最小.
∵BA=BA',MB⊥AB,
∴MA=MA'.
同理NA=NA″.
∴∠A'=∠MAB,∠A″=∠NAD.
∵∠AMN=∠A'+∠MAB=2∠A',∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A'+∠A″).
∵∠BAD=130°,
∴∠A'+∠A″=180°-∠BAD=50°.
∴∠AMN+∠ANM=2×50°=100°.
10. 【答案】C [解析] 如图,
将△ABD和△DBC分别沿着AB和BC向外翻折,得△ABG和△HBC,
连接GH,分别交AB,BC于点E,F,
此时△DEF的周长最小,即为GH的长,
∴GH=6 cm.
∵BD=6 cm,∴BG=BH=BD=6 cm=GH.
∴△BGH是等边三角形.
∴∠GBH=60°.
∴2∠ABD+2∠DBC=60°.
∴∠ABD+∠DBC=30°.
∴∠ABC=30°.故选C.
二、作图题
11. 【答案】
解:(1)如图所示.
(2)△A′B′C′如图所示,点B′的坐标为(2,1).(3)如图所示,点P的坐标为(-1,0).
12. 【答案】
解:如图,作线段AP∥l,使AP=a,且点P在点A的右侧;作点P关于直线l的对称点P',连接BP'交l于点D;在l上点D的左侧截取DC=a,则CD就是所求绿化带的位置.
13. 【答案】
解:如图,作线段AP∥l,使AP=s,且点P在点A右侧,取点P关于l的对称点P′,连接BP′交l于点D,在l上点D左侧截取DC=s,则CD即为所求绿化带的位置.
14. 【答案】
解:如图,作点A关于l1的对称点E,作点B关于l2的对称点F,连接EF,分别交l1,l2于点C,D,则折线ACDB是所求的最短路线.
15. 【答案】
解:把河流抽象成直线a,把草地抽象成直线b.
(1)如图①,过点M作MP⊥直线a于点P,则MP即为最短路线.
(2)如图②,分别作点M关于直线a,b的对称点A,B,连接AB与直线a,b分别交于点C,D,则最短的牧马路线为M→C→D→M.
三、解答题
16. 【答案】
解:(1)如图①,过点D作DF⊥BC于点F,连接EF交CD于点P,点P即为所求.
(2)如图②,过点D作DF⊥BC于点F,过点F作FE⊥AC交CD于点P,则此时PA+PE的值最小,PA+PE的最小值为线段EF的长.
∵CD是角平分线,∠BAC=∠DFC=90°,
∴DA=DF.
又∵DC=DC,∴Rt△ADC≌Rt△FDC.
∴CF=AC=10.
∵∠ACB=30°,∴EF=CF=5,即PA+PE的最小值为5.
17. 【答案】
如图①所示,MN即为所求.
[思考1] 如图②所示,折线AMNEFB即为所求.
[思考2] 如图③所示,折线AMNGHFEB即为所求.
[拓展] 如图④所示,折线AMNEFB即为所求.
一、选择题
1. 如图,A,B是两个居民小区,快递公司准备在公路l上的点P处建一个服务中心,使PA+PB最短.下面四种选址方案符合要求的是( )
2. 如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为( )
A.10 B.11 C.11.5 D.13
3. 如图,在四边形ABCD中,AB∥CD,AD⊥AB,P是AD边上的一动点,要使PC+PB的值最小,则点P应满足( )
A.PB=PC B.PA=PD
C.∠BPC=90° D.∠APB=∠DPC
4. 如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.130° B.120° C.110° D.100°
5. 如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
6. 如图,直线l是一条河,P,Q是两个村庄.欲在直线l上的某处修建一个水泵站M,向P,Q两村供水,现有如下四种铺设方案,图中PM,MQ表示铺设的管道,则所需管道最短的是( )
7. 如图,点P,Q在直线AB外,在点O沿着直线AB从左往右运动的过程中,形成无数个三角形:△O1PQ,△O2PQ,…,△OnPQ,在这样的运动变化过程中,这些三角形的周长 ( )
A.不断变大 B.不断变小
C.先变小再变大 D.先变大再变小
8. 如图,等腰三角形ABC的底边BC的长为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为( )
A.8 B.10 C.12 D.14
9. 如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则此时∠AMN+∠ANM的度数为 ( )
A.80° B.90° C.100° D.130°
10. 如图,在△ABC中,AB=BC,点D在AC上,BD=6 cm,E,F分别是AB,BC边上的动点,△DEF周长的最小值为6 cm,则∠ABC的度数为 ( )
A.20° B.25° C.30° D.35°
二、作图题
11. 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短的点P,直接写出点P的坐标.
12. 如图,在河岸l的同侧有两个居民小区A,B,现欲在河岸边建一个长为a的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图中画出绿化带的位置,并写出画图过程.
13. 河岸l同侧的两个居民小区A,B到河岸的距离分别为a米,b米(即图①中所示,AA′=a米,BB′=b米),A′B′=c米.现欲在河岸边建一个长度为s米的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.
在图②中画出绿化带的位置,并写出画图过程.
14. 如图,山娃星期天从A处赶了几只羊到草地l1放羊,然后赶羊到小河l2饮水,之后再回到B处的家,假设山娃赶羊走的都是直路,请你为他设计一条最短的路线,标明放羊与饮水的位置.
15. 如图,已知牧马营地在点M处,每天牧马人要赶着马群到河边饮水.
(1)求到河边饮水的最短路线;
(2)如果饮完水后,需再到草地吃草,然后回到营地,试设计出最短的牧马路线.
三、解答题
16. 如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图①,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图②,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并求出这个最小值.
17. 如图①所示,A,B两地在一条河的两岸,现要在河岸上造一座桥MN,桥造在何处才能使从A地到B地的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
[思考1]如图②,如果A,B两地之间有两条平行的河流,我们要建的桥都是与河岸垂直的,我们应该如何找到这个最短的路径呢?
[思考2]如图③,如果A,B两地之间有三条平行的河流呢?
[拓展]如图④,如果在上述其他条件不变的情况下,两条河并不是平行的,又该如何建桥呢?
请将你的思考在下面准备好的图形中表示出来,保留作图痕迹,将行走的路线用实线画出来.
人教版 八年级数学上册 13.4 课题学习 最短路径 同步培优-答案
一、选择题
1. 【答案】A
2. 【答案】A [解析] ∵直线m垂直平分AB,∴B,C关于直线m对称.设直线m交AB于点D,∴当点P和点D重合时,AP+CP的值最小,最小值等于AB的长,∴△APC的周长的最小值是6+4=10.
3. 【答案】D
4. 【答案】B [解析] 如图,分别作点A关于BC,DC的对称点A1,A2,连接A1A2交BC于点M,交DC于点N,则此时△AMN的周长最小.∵∠A1AA2=120°,∴∠A1+∠A2=60°.∵MA=MA1,NA=NA2,∴∠AMN+∠ANM=2(∠A1+∠A2)=2×60°=120°.
5. 【答案】C [解析] 如图,作PP′垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于点N,将P′N沿竖直方向向上平移河宽个单位长度,得到PM,PM-MN-NQ即所求.根据“两点之间,线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
6. 【答案】D
7. 【答案】C [解析] 如图,作点P关于直线AB的对称点P',连接P'Q交直线AB于点O.
∵两点之间线段最短,且PQ的长为定值,
∴当点O运动到此点时三角形的周长最短.
∴这些三角形的周长先变小再变大.
8. 【答案】D [解析] 如图,连接AD,MA.
∵△ABC是等腰三角形,D是底边BC的中点,
∴AD⊥BC.
∴S△ABC=BC·AD=×4AD=24,
解得AD=12.
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC.
∴MC+DM=MA+DM≥AD.
∴AD的长为MC+MD的最小值.
∴△CDM的周长的最小值为(MC+MD)+CD=AD+BC=12+×4=14.故选D.
9. 【答案】C [解析] 如图,延长AB到点A',使得BA'=BA,延长AD到点A″,使得DA″=AD,连接A'A″与BC,CD分别交于点M,N.
∵∠ABC=∠ADC=90°,
∴点A,A'关于BC对称,点A,A″关于CD对称,此时△AMN的周长最小.
∵BA=BA',MB⊥AB,
∴MA=MA'.
同理NA=NA″.
∴∠A'=∠MAB,∠A″=∠NAD.
∵∠AMN=∠A'+∠MAB=2∠A',∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A'+∠A″).
∵∠BAD=130°,
∴∠A'+∠A″=180°-∠BAD=50°.
∴∠AMN+∠ANM=2×50°=100°.
10. 【答案】C [解析] 如图,
将△ABD和△DBC分别沿着AB和BC向外翻折,得△ABG和△HBC,
连接GH,分别交AB,BC于点E,F,
此时△DEF的周长最小,即为GH的长,
∴GH=6 cm.
∵BD=6 cm,∴BG=BH=BD=6 cm=GH.
∴△BGH是等边三角形.
∴∠GBH=60°.
∴2∠ABD+2∠DBC=60°.
∴∠ABD+∠DBC=30°.
∴∠ABC=30°.故选C.
二、作图题
11. 【答案】
解:(1)如图所示.
(2)△A′B′C′如图所示,点B′的坐标为(2,1).(3)如图所示,点P的坐标为(-1,0).
12. 【答案】
解:如图,作线段AP∥l,使AP=a,且点P在点A的右侧;作点P关于直线l的对称点P',连接BP'交l于点D;在l上点D的左侧截取DC=a,则CD就是所求绿化带的位置.
13. 【答案】
解:如图,作线段AP∥l,使AP=s,且点P在点A右侧,取点P关于l的对称点P′,连接BP′交l于点D,在l上点D左侧截取DC=s,则CD即为所求绿化带的位置.
14. 【答案】
解:如图,作点A关于l1的对称点E,作点B关于l2的对称点F,连接EF,分别交l1,l2于点C,D,则折线ACDB是所求的最短路线.
15. 【答案】
解:把河流抽象成直线a,把草地抽象成直线b.
(1)如图①,过点M作MP⊥直线a于点P,则MP即为最短路线.
(2)如图②,分别作点M关于直线a,b的对称点A,B,连接AB与直线a,b分别交于点C,D,则最短的牧马路线为M→C→D→M.
三、解答题
16. 【答案】
解:(1)如图①,过点D作DF⊥BC于点F,连接EF交CD于点P,点P即为所求.
(2)如图②,过点D作DF⊥BC于点F,过点F作FE⊥AC交CD于点P,则此时PA+PE的值最小,PA+PE的最小值为线段EF的长.
∵CD是角平分线,∠BAC=∠DFC=90°,
∴DA=DF.
又∵DC=DC,∴Rt△ADC≌Rt△FDC.
∴CF=AC=10.
∵∠ACB=30°,∴EF=CF=5,即PA+PE的最小值为5.
17. 【答案】
如图①所示,MN即为所求.
[思考1] 如图②所示,折线AMNEFB即为所求.
[思考2] 如图③所示,折线AMNGHFEB即为所求.
[拓展] 如图④所示,折线AMNEFB即为所求.
