人教版 九年级数学上册 23.1 图形的旋转 同步培优(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 23.1 图形的旋转 同步培优(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 710.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览



文档简介
人教版 九年级数学上册 23.1 图形的旋转 同步培优
一、选择题
1. 将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
2. 在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
3. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB
C.BC=DE D.∠A=∠EBC
4. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-1,2+) B.(-,3)
C.(-,2+) D.(-3,)
5. 如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
图7-ZT-1
A.(-1,2+) B.(-,3)
C.(-,2+) D.(-3,)
6. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
7. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α C.180°-α D.2α
8. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4 B.3 C.2 D.1
二、填空题
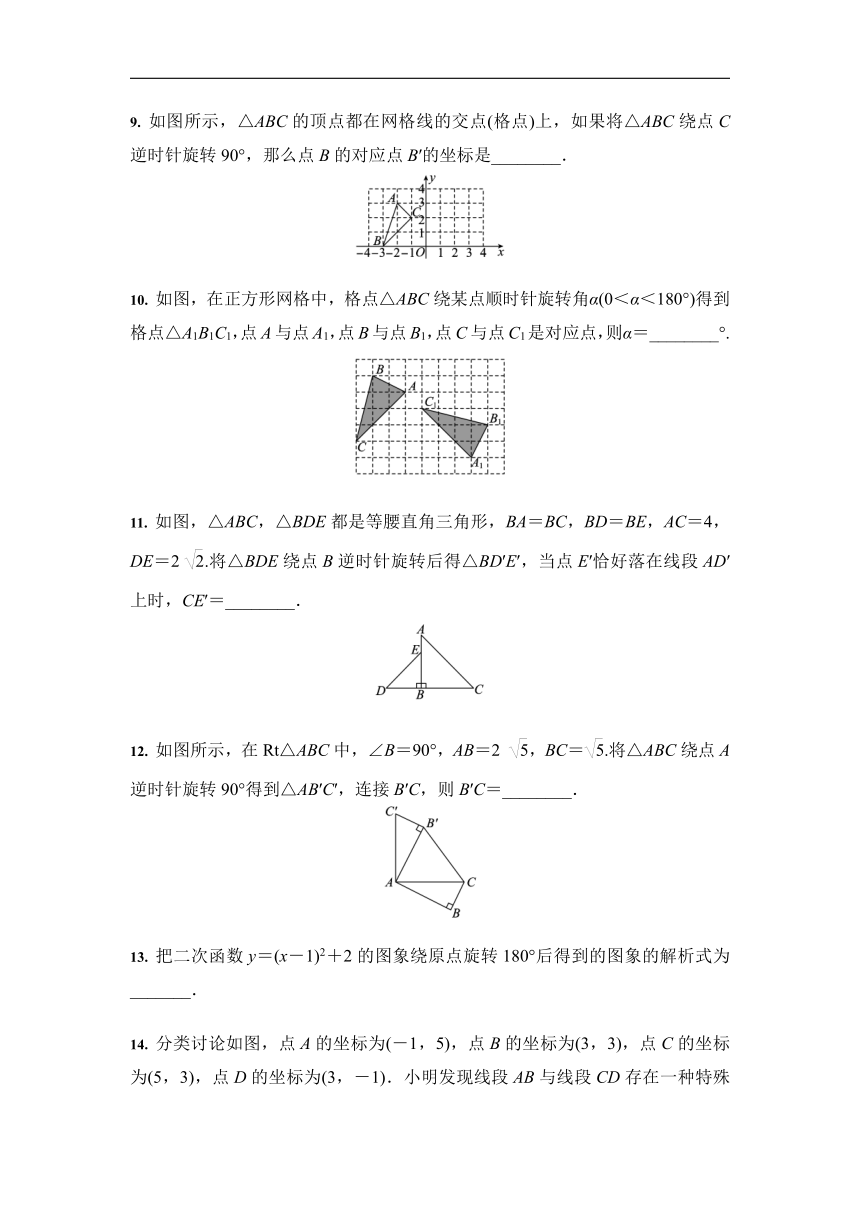
9. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
10. 如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=________°.
11. 如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
12. 如图所示,在Rt△ABC中,∠B=90°,AB=2 ,BC=.将△ABC绕点A逆时针旋转90°得到△AB′C′,连接B′C,则B′C=________.
13. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
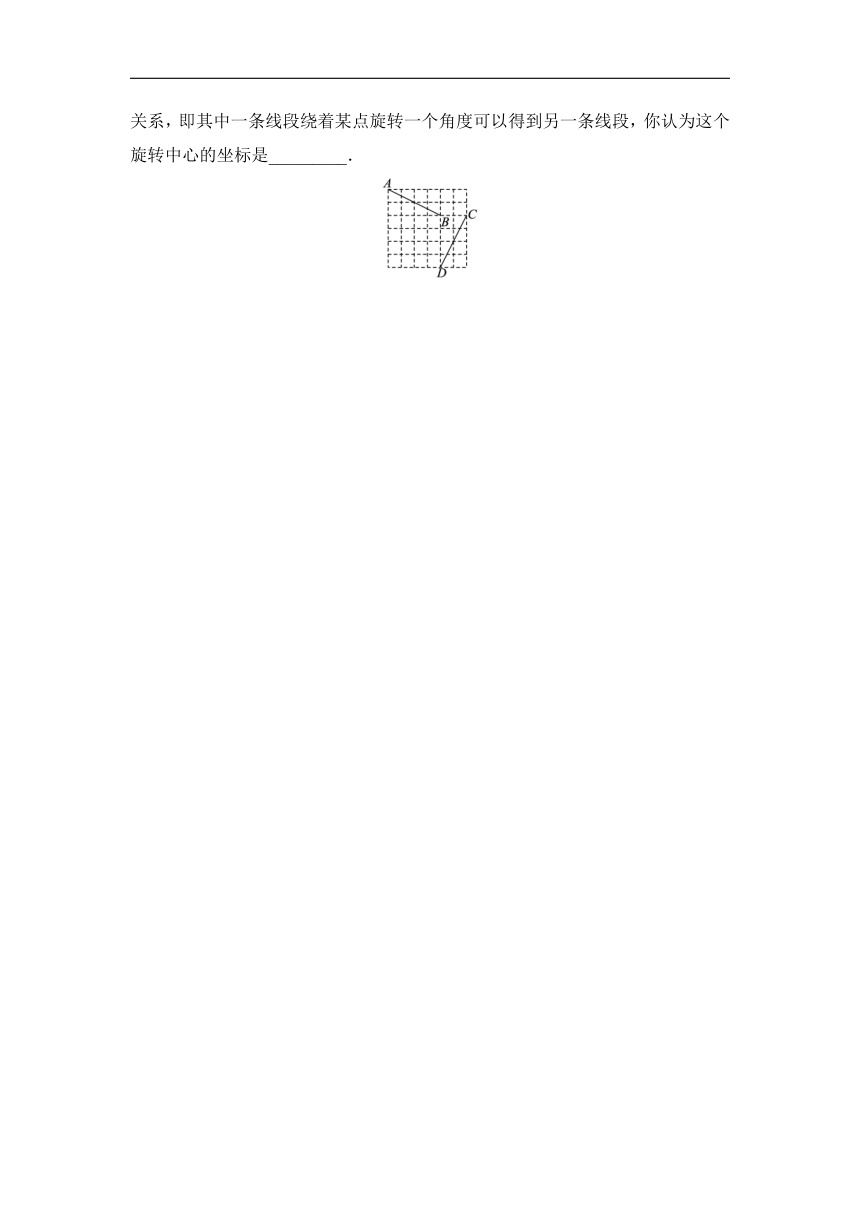
14. 分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
15. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
16. 如图,在△ABC中,∠BAC=90°,AB=AC=10 cm,D为△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A逆时针旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为________ cm.
三、作图题
17. 如图,网格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移2个单位长度,点A的对应点为A1,点B的对应点为B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1逆时针旋转90°,点B1的对应点为B2,请画出旋转后的线段A1B2;
(3)连接AB2,BB2,求△ABB2的面积.
18. 图是由边长为1的小正方形组成的8×4的网格,每个小正方形的顶点叫做格点.点A,B,C,D均在格点上,在网格中将点D按下列步骤移动:
第一步:点D绕点A顺时针旋转180°得到点D1;
第二步:点D1绕点B顺时针旋转90°得到点D2;
第三步:点D2绕点C顺时针旋转90°回到点D.
(1)请用圆规画出点D→D1→D2→D经过的路径;
(2)所画图形是________对称图形;
(3)求所画图形的周长(结果保留π).
四、解答题
19. 如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
20. 如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外部的点D1处转到其内部的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
21. (1)如图 (a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
22. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学上册 23.1 图形的旋转 同步培优-答案
一、选择题
1. 【答案】D [解析] 平行四边形绕其对角线的交点旋转能够与原来的图形重合的最小旋转角度数是180°,故A错误;矩形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故B错误;菱形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故C错误;正方形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是90°.故选D.
2. 【答案】A [解析] 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
3. 【答案】D [解析] 由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
4. 【答案】B
5. 【答案】B [解析] 如图,过点B′作B′H⊥y轴于点H.
由题意得,OA′=A′B′=2,∠B′A′H=60°,
∴∠A′B′H=30°,
∴AH′=A′B′=1,B′H=,
∴OH=3,∴B′(-,3).
6. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
7. 【答案】C [解析] 由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
8. 【答案】B [解析] 连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
9. 【答案】(1,0)
10. 【答案】90 [解析] 连接AA1,CC1,分别作AA1和CC1的垂直平分线,两直线相交于点D,则点D即为旋转中心,连接AD,A1D,则∠ADA1=α=90°.
11. 【答案】+ [解析] 如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
12. 【答案】5 [解析] 由勾股定理,得AC==5.过点C作CE⊥AB′于点E,则四边形ABCE是矩形,∴AE=BC=.又AB′=AB=2 ,∴AE=EB′=,∴CE垂直平分AB′,∴B′C=AC=5.
13. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14. 【答案】(4,4)或(1,1)
[解析] (1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
15. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
16. 【答案】(10-2 ) [解析] 如图,过点A作AG⊥DE于点G.由旋转知,AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,
∴∠AED=∠ADG=45°,
∴∠AFD=∠AED+∠CAE=60°.
在Rt△ADG中,AG=DG==3 (cm).
在Rt△AFG中,GF==(cm),AF=2FG=2 (cm),
∴CF=AC-AF=(10-2 )cm.
三、作图题
17. 【答案】
解:(1)如图,线段A1B1即为所求.
(2)如图,线段A1B2即为所求.
(3)如图,S△ABB2=4×4-×2×4-×2×2-×2×4=6.
18. 【答案】
解:(1)如图所示:
(2)轴
(3)所画图形的周长=半径为4的圆的周长=2π×4=8π.
四、解答题
19. 【答案】
解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,∴∠DCE=∠DCF.
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,∴DE2=AD2+BE2=32+22=13,
∴DE=.
20. 【答案】
解:(1)①当A,D,M三点在同一直线上时,AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,显然∠MAD不能为直角.
当∠AMD为直角时,AM2=AD2-DM2=302-102=800,∵AM>0,
∴AM=20 .
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,∵AM>0,
∴AM=10 .
综上所述,满足条件的AM的长为20 或10 .
(2)如图,连接CD1,
由题意得,∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30 .
∵∠AD2C=135°,
∴∠CD2D1=∠AD2C-∠AD2D1=90°,
∴CD1==30 .
∵∠BAC=∠D1AD2=90°,
∴∠BAC-∠CAD2=∠D1AD2-∠CAD2,
∴∠BAD2=∠CAD1.
又∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30 .
21. 【答案】
解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE.
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
22. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
一、选择题
1. 将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
2. 在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
3. 如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD B.AB⊥EB
C.BC=DE D.∠A=∠EBC
4. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-1,2+) B.(-,3)
C.(-,2+) D.(-3,)
5. 如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
图7-ZT-1
A.(-1,2+) B.(-,3)
C.(-,2+) D.(-3,)
6. 在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1) B.(,-1) C.(2,1) D.(0,2)
7. 如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α B.α C.180°-α D.2α
8. 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4 B.3 C.2 D.1
二、填空题
9. 如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
10. 如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=________°.
11. 如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
12. 如图所示,在Rt△ABC中,∠B=90°,AB=2 ,BC=.将△ABC绕点A逆时针旋转90°得到△AB′C′,连接B′C,则B′C=________.
13. 把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
14. 分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
15. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
16. 如图,在△ABC中,∠BAC=90°,AB=AC=10 cm,D为△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A逆时针旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为________ cm.
三、作图题
17. 如图,网格纸上每个小正方形的边长均为1个单位长度,点A,B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移2个单位长度,点A的对应点为A1,点B的对应点为B1,请画出平移后的线段A1B1;
(2)将线段A1B1绕点A1逆时针旋转90°,点B1的对应点为B2,请画出旋转后的线段A1B2;
(3)连接AB2,BB2,求△ABB2的面积.
18. 图是由边长为1的小正方形组成的8×4的网格,每个小正方形的顶点叫做格点.点A,B,C,D均在格点上,在网格中将点D按下列步骤移动:
第一步:点D绕点A顺时针旋转180°得到点D1;
第二步:点D1绕点B顺时针旋转90°得到点D2;
第三步:点D2绕点C顺时针旋转90°回到点D.
(1)请用圆规画出点D→D1→D2→D经过的路径;
(2)所画图形是________对称图形;
(3)求所画图形的周长(结果保留π).
四、解答题
19. 如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
20. 如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外部的点D1处转到其内部的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
21. (1)如图 (a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
22. 已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版 九年级数学上册 23.1 图形的旋转 同步培优-答案
一、选择题
1. 【答案】D [解析] 平行四边形绕其对角线的交点旋转能够与原来的图形重合的最小旋转角度数是180°,故A错误;矩形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故B错误;菱形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是180°,故C错误;正方形绕其对角线的交点旋转,能够与原来的图形重合的最小旋转角度数是90°.故选D.
2. 【答案】A [解析] 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
3. 【答案】D [解析] 由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
4. 【答案】B
5. 【答案】B [解析] 如图,过点B′作B′H⊥y轴于点H.
由题意得,OA′=A′B′=2,∠B′A′H=60°,
∴∠A′B′H=30°,
∴AH′=A′B′=1,B′H=,
∴OH=3,∴B′(-,3).
6. 【答案】A [解析] 如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
7. 【答案】C [解析] 由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
8. 【答案】B [解析] 连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
9. 【答案】(1,0)
10. 【答案】90 [解析] 连接AA1,CC1,分别作AA1和CC1的垂直平分线,两直线相交于点D,则点D即为旋转中心,连接AD,A1D,则∠ADA1=α=90°.
11. 【答案】+ [解析] 如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
12. 【答案】5 [解析] 由勾股定理,得AC==5.过点C作CE⊥AB′于点E,则四边形ABCE是矩形,∴AE=BC=.又AB′=AB=2 ,∴AE=EB′=,∴CE垂直平分AB′,∴B′C=AC=5.
13. 【答案】y=-x2-2x-3 [解析] 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14. 【答案】(4,4)或(1,1)
[解析] (1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
15. 【答案】18 [解析] 如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
16. 【答案】(10-2 ) [解析] 如图,过点A作AG⊥DE于点G.由旋转知,AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,
∴∠AED=∠ADG=45°,
∴∠AFD=∠AED+∠CAE=60°.
在Rt△ADG中,AG=DG==3 (cm).
在Rt△AFG中,GF==(cm),AF=2FG=2 (cm),
∴CF=AC-AF=(10-2 )cm.
三、作图题
17. 【答案】
解:(1)如图,线段A1B1即为所求.
(2)如图,线段A1B2即为所求.
(3)如图,S△ABB2=4×4-×2×4-×2×2-×2×4=6.
18. 【答案】
解:(1)如图所示:
(2)轴
(3)所画图形的周长=半径为4的圆的周长=2π×4=8π.
四、解答题
19. 【答案】
解:如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,∴∠DCE=∠DCF.
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,∴DE2=AD2+BE2=32+22=13,
∴DE=.
20. 【答案】
解:(1)①当A,D,M三点在同一直线上时,AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,显然∠MAD不能为直角.
当∠AMD为直角时,AM2=AD2-DM2=302-102=800,∵AM>0,
∴AM=20 .
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,∵AM>0,
∴AM=10 .
综上所述,满足条件的AM的长为20 或10 .
(2)如图,连接CD1,
由题意得,∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30 .
∵∠AD2C=135°,
∴∠CD2D1=∠AD2C-∠AD2D1=90°,
∴CD1==30 .
∵∠BAC=∠D1AD2=90°,
∴∠BAC-∠CAD2=∠D1AD2-∠CAD2,
∴∠BAD2=∠CAD1.
又∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30 .
21. 【答案】
解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE.
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
22. 【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
同课章节目录
