1.1变化率与导数 课时同步练习(含解析)
文档属性
| 名称 | 1.1变化率与导数 课时同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 11:26:25 | ||
图片预览




文档简介
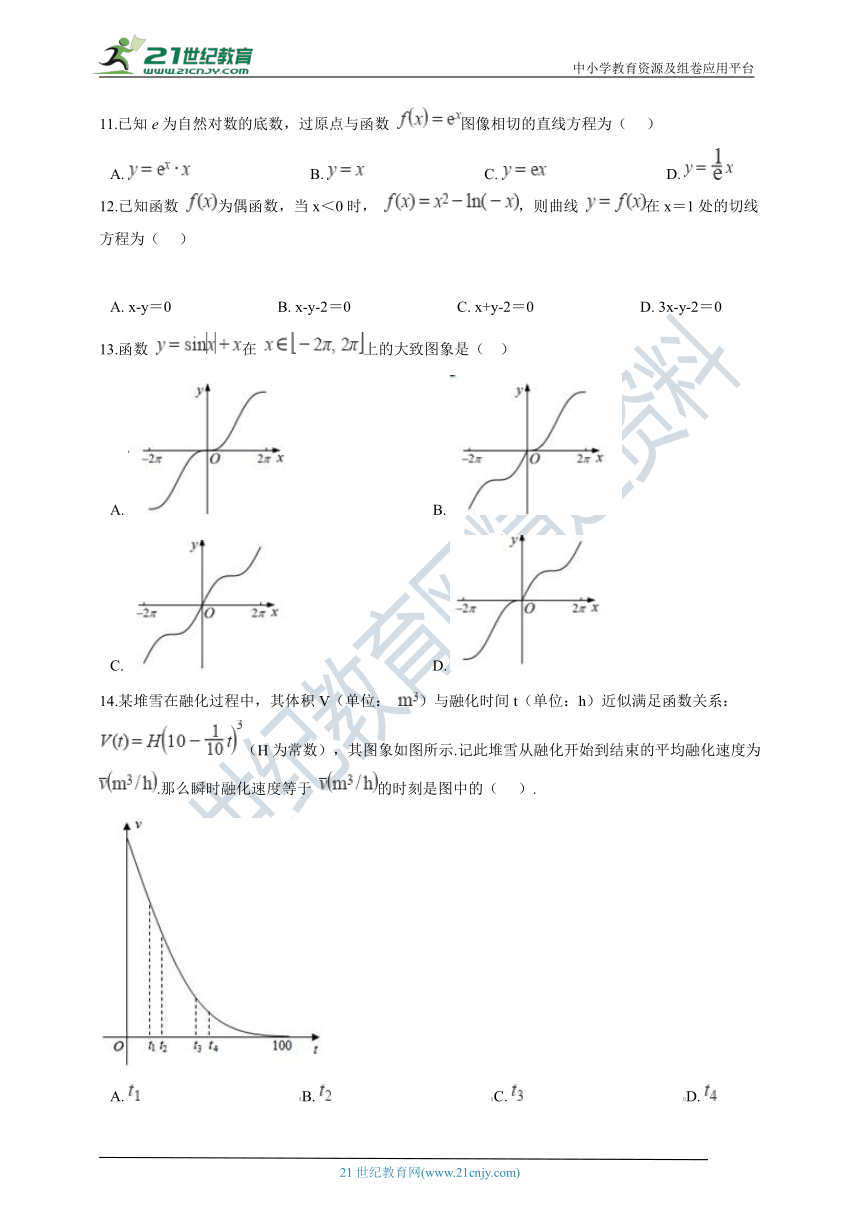
中小学教育资源及组卷应用平台
高中数学人教新课标A版
选修2-2
1.1变化率与导数
一、单选题
1.函数
在区间
上的平均变化率为3,则实数m的值为(???
)
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
2.一个物体的位移s(米)和与时间
(秒)的关系为
,则该物体在4秒末的瞬时速度是
(
????)
A.?12米/秒???????????????????????????????B.?8米/秒???????????????????????????????C.?6米/秒???????????????????????????????D.?8米/秒
3.若直线
与曲线
(
,e为自然对数的底数)相切,则
(???
)
A.?-2????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?2
4.曲线
在点
处的切线方程为
,则
(??
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?4?????????????????????????????????????????D.?8
5.函数
在区间
上的平均变化率为(???
)
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
6.某物体沿水平方向运动,其前进距离s(米)与时间t(秒)的关系为
,则该物体在运行前2秒的平均速度为(???
)(米/秒)
A.?18?????????????????????????????????????????B.?13?????????????????????????????????????????C.?9?????????????????????????????????????????D.?
7.曲线
在
处的切线方程是(??
)
A.?????????????????B.?????????????????C.?????????????????D.?
8.若
,则
等于(??
)
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?3???????????????????????????????????????????D.?
9.曲线
在点
处的切线斜率为(????
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
10.若曲线
(
)存在斜率小于1的切线,则a的取值范围为(???
)
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
11.已知e为自然对数的底数,过原点与函数
图像相切的直线方程为(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
12.已知函数
为偶函数,当x<0时,
,则曲线
在x=1处的切线方程为(???
)
A.?x-y=0????????????????????????????B.?x-y-2=0????????????????????????????C.?x+y-2=0????????????????????????????D.?3x-y-2=0
13.函数
在
上的大致图象是(??
)
A.??????????????????????????????????????B.?
C.?????????????????????????????????????D.?
14.某堆雪在融化过程中,其体积V(单位:
)与融化时间t(单位:h)近似满足函数关系:
(H为常数),其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为
.那么瞬时融化速度等于
的时刻是图中的(???
).
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
15.已知直线
是曲线
的一条切线,则
________.
16.若一汽车在公路上做加速运动,设
秒时的速度为
,则该车在
时的加速度为________.
17.如图,直线
是曲线
在
处的切线,则
________.
18.已知函数
在区间
,
上的平均变化率分别为
,
,那么
,
的大小关系为________.
19.已知定义在R上的奇函数
,当
时,
,则
在点
处的切线方程为________.
20.点P(4,4)为曲线C:
上一点,过P作直线PQ交曲线C于点Q(异于P点),P与曲线C的焦点F的连线与Q点处的切线l垂直,直线l与曲线C的准线交于点M
,
则
________
三、解答题
21.求下列函数的导数
(1)y=2x3﹣3x2﹣4;
(2)y=xlnx;
(3)
物体作直线运动的方程s=t2+2t﹣3,求物体在t=2秒时的速度和加速度.
已知函数
,求曲线
在点
处的切线方程.
24.已知曲线
y
=
x3
+
x-2
在点
P0
处的切线
平行于直线4x-y-1=0,且点
P0
在第三象限,
(1)求P0的坐标;
(2)若直线
,
且
l
也过切点P0
,求直线l的方程.
答案解析部分
一、单选题
1.答案:
D
解:根据题意,函数
在区间
上的平均变化率为
,
则有
,解可得:
.
故答案为:D
【分析】据题意,求出函数在间
上的平均变化率,进而可得
,解可得m的值,即可得答案.
2.答案:
C
解:∵一个物体的位移s(米)和与时间t(秒)的关系为s=4-2t+t2
,
∴s′=2t-2,
∴该物体在4秒末的瞬时速度是s′|x=4=2×4-2=6.
故答案为:C.
【分析】瞬时速度问题的研究一般借助函数的导数求其某一时刻的瞬时速度,先求s=4-2t+t2的导数,再求得t=4秒时的导数,即可得到所求的瞬时速度.
3.答案:
B
解:不妨设切点为
,因为
,
故可得
,
,
,
解得
,故可得
,
解得
.
故答案为:B.
【分析】设出切点,利用导数几何意义,列出方程,即可求得参数m.
4.答案:
B
解:因为
,
所以
,
故
,解得
,
又切线过点
,所以
,解得
,所以
,
故答案为:B
【分析】求函数导数,利用切线斜率求出a,根据切线过点
求出b即可.
5.答案:
B
解:因为
,
所以
在区间
上的平均变化率为
.
故选:B
【分析】直接利用平均变化率公式
进行求值.
6.答案:
C
解:
,因此该物体在运行前2秒的平均速度为
(米/秒).
故答案为:C.
【分析】利用平均变化率的定义得出该物体在运行前2秒的平均速度为
,进而可求得结果.
7.答案:
D
解:由题意知,
,
在
处的切线的斜率
,
则在
处的切线方程是:
,
即
,
故答案为:
.
【分析】先求出导数,再把
代入求出切线的斜率,代入点斜式方程并化为一般式.
8.答案:
B
解:根据题意,若
,
则
,
即
.
故答案为:
.
【分析】根据题意,由导数的定义可得答案.
9.答案:
D
解:
,则
,
.
故答案为:D.
【分析】求出导数后即可得切线斜率.
10.答案:
C
解:由题意可得
在
上有解,
设
(
),
,
令
,得
;令
,得
,
在
单调递减,在
单调递增,
,解得:
.
故答案为:C.
【分析】对函数进行求导,将问题转化为不等式有解问题,再构造函数利用导数研究函数的最值,即可得答案;
11.答案:
C
解:设切点为
,因为
,故在
切线的斜率为
.又切线经过原点.
且
在
上.故
.
故斜率
.所以切线方程为
.
故选:C
【分析】设切点为
再根据导数的几何意义列式求解即可.
12.答案:
A
解:当
时,
,
,
又函数
为偶函数,所以
,
,所以
,
,
故切线方程为
,即
.
故答案为:A.
【分析】先求出当
时,
的解析式,再利用导数的几何意义计算即可得到答案.
13.答案:
D
解:当
时,
,则
,
所以函数在
上单调递增,
令
,则
,
根据三角函数的性质,
当
时,
,故切线的斜率变小,
当
时,
,故切线的斜率变大,可排除A、B;
当
时,
,则
,
所以函数在
上单调递增,
令
,
,
当
时,
,故切线的斜率变大,
当
时,
,故切线的斜率变小,可排除C,
故答案为:D
【分析】讨论
的取值范围,然后对函数进行求导,利用导数的几何意义即可判断.
14.答案:
C
解:平均融化速度为
,
反映的是
图象与坐标轴交点连线的斜率,
观察可知
处瞬时速度(即切线的斜率)为平均速度一致,
故答案为:C.
【分析】根据题意可知,平均融化速度反映的是
图象与坐标轴交点连线的斜率,通过观察某一时刻处瞬时速度(即切线的斜率),即可得到答案.
二、填空题
15.答案:
4
解:设
,切点为
,
因为
,所以
,解得
,
所以
,
故切点为
,又切点在切线
上,故
.
故答案为:4
【分析】设切点为
,根据导数的几何意义可求斜率
,即可求出
,代入切线方程即可求解.
16.答案:
解:根据加速度等于速度的导数可知:
,
?
该车在
时的加速度为
.
故答案为:
【分析】由速度函数的导函数即为加速度可知,求导代值即可.
17.答案:
解:由图可知直线
过点
,
可求出直线
的斜率
,
由导数的几何意义可知,
.
故答案为:
.
【分析】求出切线
的斜率,即可求出结论.
18.答案:
k1>k2
解:当
,
时,平均变化率
,
当
,
时,平均变化率
,
则,
故答案为:
.
【分析】根据平均变化率列出相应的式子,在讨论自变量的情况下,比较两个数的大小.
19.答案:
解:当
时,
,
,
,
,
切线方程为
,即
.
故答案为:
.
【分析】根据奇函数的性质求出当
时函数的解析式,利用导数的几何意义求切线的方程.
20.答案:
解:P=
,即
,即
,导函数
,
所以焦点F(0,1),准线为y=-1;直线PF的斜率k1=
,
则Q(x1
,
y1)处切线l的斜率k=
;
依题意得kk1=-1,
;所以
.
切线l的方程为
,与准线的交点M(
).
所以,
.
故答案为:
【分析】根据抛物线上点的坐标求出抛物线方程,根据斜率求出切线l的斜率,求出点Q的坐标,即可得解.
三、解答题
21.答案:
(1)解:y′=6x2﹣6x;
(2)解:y′=lnx+1;
(3)解:
.
【分析】直接利用和、差、积商的导数公式,即可得出结论.
答案:解:由导数的物理意义:物体作直线运动的方程s=s(t)
,
则物体在t=t0时的即时速度v=s′(t0),
在t=t0时的加速度a=s″(t0),
∴v=s′(t)=2t+2?,a=s″(t)=2,
物体在t=2秒时的速度v=s′(2)=(2t+2)|t=2=6,
加速度a=s″(t)=2|t=2=2
.
【分析】首先求导,然后将t=2代入即可得到速度;再次求导,然后将t=2代入即可得到加速度.
23.答案:
解:依题意可知:
,
,
∴切线方程为
,即
.
【分析】先求出函数的导数在
处的导数值(切线的斜率),再利用点斜式求出曲线
在点
处切线的方程,最后化为一般式即可.
24.答案:
(1)解:由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.
当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为(-1,-4);
(2)解:∵直线
l⊥l1
,
l1的斜率为4,
∴直线l的斜率为-1/
4
,
∵l过切点P0
,
点P0的坐标为(-1,-4)
∴直线l的方程为y+4=
(x+1)即x+4y+17=0.
【分析】本试题主要是考查了导数的几何意义,两条直线的位置关系,平行和垂直的运用。以及直线方程的求解的综合运用。首先根据已知条件,利用导数定义,得到点P0的坐标,然后利用
,设出方程为x+4y+c=0,根据直线过点P0得到结论.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
高中数学人教新课标A版
选修2-2
1.1变化率与导数
一、单选题
1.函数
在区间
上的平均变化率为3,则实数m的值为(???
)
A.?5???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
2.一个物体的位移s(米)和与时间
(秒)的关系为
,则该物体在4秒末的瞬时速度是
(
????)
A.?12米/秒???????????????????????????????B.?8米/秒???????????????????????????????C.?6米/秒???????????????????????????????D.?8米/秒
3.若直线
与曲线
(
,e为自然对数的底数)相切,则
(???
)
A.?-2????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?2
4.曲线
在点
处的切线方程为
,则
(??
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.?4?????????????????????????????????????????D.?8
5.函数
在区间
上的平均变化率为(???
)
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
6.某物体沿水平方向运动,其前进距离s(米)与时间t(秒)的关系为
,则该物体在运行前2秒的平均速度为(???
)(米/秒)
A.?18?????????????????????????????????????????B.?13?????????????????????????????????????????C.?9?????????????????????????????????????????D.?
7.曲线
在
处的切线方程是(??
)
A.?????????????????B.?????????????????C.?????????????????D.?
8.若
,则
等于(??
)
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?3???????????????????????????????????????????D.?
9.曲线
在点
处的切线斜率为(????
)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
10.若曲线
(
)存在斜率小于1的切线,则a的取值范围为(???
)
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
11.已知e为自然对数的底数,过原点与函数
图像相切的直线方程为(???
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
12.已知函数
为偶函数,当x<0时,
,则曲线
在x=1处的切线方程为(???
)
A.?x-y=0????????????????????????????B.?x-y-2=0????????????????????????????C.?x+y-2=0????????????????????????????D.?3x-y-2=0
13.函数
在
上的大致图象是(??
)
A.??????????????????????????????????????B.?
C.?????????????????????????????????????D.?
14.某堆雪在融化过程中,其体积V(单位:
)与融化时间t(单位:h)近似满足函数关系:
(H为常数),其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为
.那么瞬时融化速度等于
的时刻是图中的(???
).
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
15.已知直线
是曲线
的一条切线,则
________.
16.若一汽车在公路上做加速运动,设
秒时的速度为
,则该车在
时的加速度为________.
17.如图,直线
是曲线
在
处的切线,则
________.
18.已知函数
在区间
,
上的平均变化率分别为
,
,那么
,
的大小关系为________.
19.已知定义在R上的奇函数
,当
时,
,则
在点
处的切线方程为________.
20.点P(4,4)为曲线C:
上一点,过P作直线PQ交曲线C于点Q(异于P点),P与曲线C的焦点F的连线与Q点处的切线l垂直,直线l与曲线C的准线交于点M
,
则
________
三、解答题
21.求下列函数的导数
(1)y=2x3﹣3x2﹣4;
(2)y=xlnx;
(3)
物体作直线运动的方程s=t2+2t﹣3,求物体在t=2秒时的速度和加速度.
已知函数
,求曲线
在点
处的切线方程.
24.已知曲线
y
=
x3
+
x-2
在点
P0
处的切线
平行于直线4x-y-1=0,且点
P0
在第三象限,
(1)求P0的坐标;
(2)若直线
,
且
l
也过切点P0
,求直线l的方程.
答案解析部分
一、单选题
1.答案:
D
解:根据题意,函数
在区间
上的平均变化率为
,
则有
,解可得:
.
故答案为:D
【分析】据题意,求出函数在间
上的平均变化率,进而可得
,解可得m的值,即可得答案.
2.答案:
C
解:∵一个物体的位移s(米)和与时间t(秒)的关系为s=4-2t+t2
,
∴s′=2t-2,
∴该物体在4秒末的瞬时速度是s′|x=4=2×4-2=6.
故答案为:C.
【分析】瞬时速度问题的研究一般借助函数的导数求其某一时刻的瞬时速度,先求s=4-2t+t2的导数,再求得t=4秒时的导数,即可得到所求的瞬时速度.
3.答案:
B
解:不妨设切点为
,因为
,
故可得
,
,
,
解得
,故可得
,
解得
.
故答案为:B.
【分析】设出切点,利用导数几何意义,列出方程,即可求得参数m.
4.答案:
B
解:因为
,
所以
,
故
,解得
,
又切线过点
,所以
,解得
,所以
,
故答案为:B
【分析】求函数导数,利用切线斜率求出a,根据切线过点
求出b即可.
5.答案:
B
解:因为
,
所以
在区间
上的平均变化率为
.
故选:B
【分析】直接利用平均变化率公式
进行求值.
6.答案:
C
解:
,因此该物体在运行前2秒的平均速度为
(米/秒).
故答案为:C.
【分析】利用平均变化率的定义得出该物体在运行前2秒的平均速度为
,进而可求得结果.
7.答案:
D
解:由题意知,
,
在
处的切线的斜率
,
则在
处的切线方程是:
,
即
,
故答案为:
.
【分析】先求出导数,再把
代入求出切线的斜率,代入点斜式方程并化为一般式.
8.答案:
B
解:根据题意,若
,
则
,
即
.
故答案为:
.
【分析】根据题意,由导数的定义可得答案.
9.答案:
D
解:
,则
,
.
故答案为:D.
【分析】求出导数后即可得切线斜率.
10.答案:
C
解:由题意可得
在
上有解,
设
(
),
,
令
,得
;令
,得
,
在
单调递减,在
单调递增,
,解得:
.
故答案为:C.
【分析】对函数进行求导,将问题转化为不等式有解问题,再构造函数利用导数研究函数的最值,即可得答案;
11.答案:
C
解:设切点为
,因为
,故在
切线的斜率为
.又切线经过原点.
且
在
上.故
.
故斜率
.所以切线方程为
.
故选:C
【分析】设切点为
再根据导数的几何意义列式求解即可.
12.答案:
A
解:当
时,
,
,
又函数
为偶函数,所以
,
,所以
,
,
故切线方程为
,即
.
故答案为:A.
【分析】先求出当
时,
的解析式,再利用导数的几何意义计算即可得到答案.
13.答案:
D
解:当
时,
,则
,
所以函数在
上单调递增,
令
,则
,
根据三角函数的性质,
当
时,
,故切线的斜率变小,
当
时,
,故切线的斜率变大,可排除A、B;
当
时,
,则
,
所以函数在
上单调递增,
令
,
,
当
时,
,故切线的斜率变大,
当
时,
,故切线的斜率变小,可排除C,
故答案为:D
【分析】讨论
的取值范围,然后对函数进行求导,利用导数的几何意义即可判断.
14.答案:
C
解:平均融化速度为
,
反映的是
图象与坐标轴交点连线的斜率,
观察可知
处瞬时速度(即切线的斜率)为平均速度一致,
故答案为:C.
【分析】根据题意可知,平均融化速度反映的是
图象与坐标轴交点连线的斜率,通过观察某一时刻处瞬时速度(即切线的斜率),即可得到答案.
二、填空题
15.答案:
4
解:设
,切点为
,
因为
,所以
,解得
,
所以
,
故切点为
,又切点在切线
上,故
.
故答案为:4
【分析】设切点为
,根据导数的几何意义可求斜率
,即可求出
,代入切线方程即可求解.
16.答案:
解:根据加速度等于速度的导数可知:
,
?
该车在
时的加速度为
.
故答案为:
【分析】由速度函数的导函数即为加速度可知,求导代值即可.
17.答案:
解:由图可知直线
过点
,
可求出直线
的斜率
,
由导数的几何意义可知,
.
故答案为:
.
【分析】求出切线
的斜率,即可求出结论.
18.答案:
k1>k2
解:当
,
时,平均变化率
,
当
,
时,平均变化率
,
则,
故答案为:
.
【分析】根据平均变化率列出相应的式子,在讨论自变量的情况下,比较两个数的大小.
19.答案:
解:当
时,
,
,
,
,
切线方程为
,即
.
故答案为:
.
【分析】根据奇函数的性质求出当
时函数的解析式,利用导数的几何意义求切线的方程.
20.答案:
解:P=
,即
,即
,导函数
,
所以焦点F(0,1),准线为y=-1;直线PF的斜率k1=
,
则Q(x1
,
y1)处切线l的斜率k=
;
依题意得kk1=-1,
;所以
.
切线l的方程为
,与准线的交点M(
).
所以,
.
故答案为:
【分析】根据抛物线上点的坐标求出抛物线方程,根据斜率求出切线l的斜率,求出点Q的坐标,即可得解.
三、解答题
21.答案:
(1)解:y′=6x2﹣6x;
(2)解:y′=lnx+1;
(3)解:
.
【分析】直接利用和、差、积商的导数公式,即可得出结论.
答案:解:由导数的物理意义:物体作直线运动的方程s=s(t)
,
则物体在t=t0时的即时速度v=s′(t0),
在t=t0时的加速度a=s″(t0),
∴v=s′(t)=2t+2?,a=s″(t)=2,
物体在t=2秒时的速度v=s′(2)=(2t+2)|t=2=6,
加速度a=s″(t)=2|t=2=2
.
【分析】首先求导,然后将t=2代入即可得到速度;再次求导,然后将t=2代入即可得到加速度.
23.答案:
解:依题意可知:
,
,
∴切线方程为
,即
.
【分析】先求出函数的导数在
处的导数值(切线的斜率),再利用点斜式求出曲线
在点
处切线的方程,最后化为一般式即可.
24.答案:
(1)解:由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.
当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为(-1,-4);
(2)解:∵直线
l⊥l1
,
l1的斜率为4,
∴直线l的斜率为-1/
4
,
∵l过切点P0
,
点P0的坐标为(-1,-4)
∴直线l的方程为y+4=
(x+1)即x+4y+17=0.
【分析】本试题主要是考查了导数的几何意义,两条直线的位置关系,平行和垂直的运用。以及直线方程的求解的综合运用。首先根据已知条件,利用导数定义,得到点P0的坐标,然后利用
,设出方程为x+4y+c=0,根据直线过点P0得到结论.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
