第五章三角形第七课时全等三角形的概念和性质
文档属性
| 名称 | 第五章三角形第七课时全等三角形的概念和性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 17.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览


文档简介
三角形
XX中学 XXX 审核人:XXX
【学习课题】 第7课时 全等三角形的概念和性质
【学习目标】 1、图形全等的相关概念及性质;
2、能说出什么叫全等三角形,知道如何表示两个三角形全等;
3、能找出全等三角形的对应元素;
4、能应用“全等三角形对应边相等、对应角相等”的性质解决问题。
【学习重点】全等三角形对应边相等、对应角相等的性质,并能进行简单的推理和计算。
【学习难点】熟练应用全等三角形的性质解决问题。
【学习过程】
学习准备: 1、阅读教材148—150,153—154; 2、纸张、剪刀
解读教材:
1、阅读课本148—150,
(1)图形全等的概念:
(2)图形全等的性质:
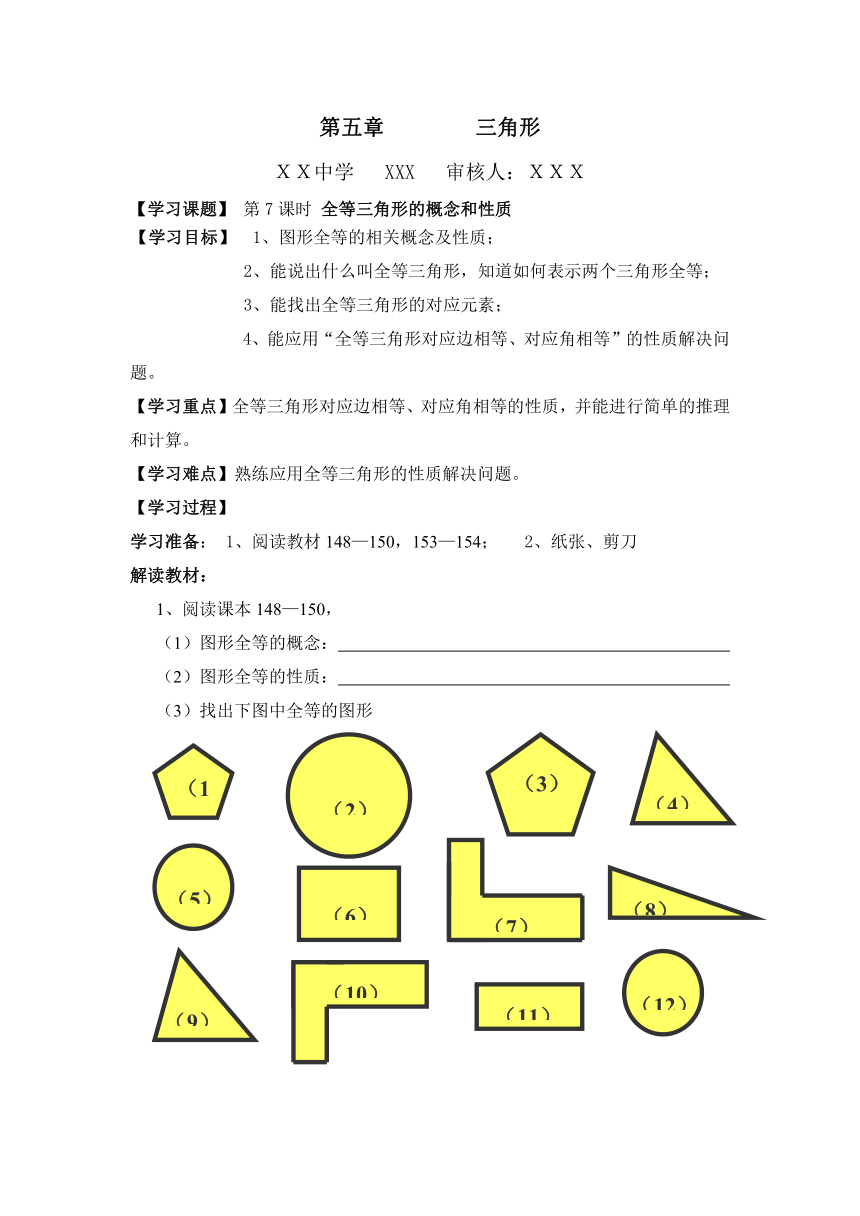
(3)找出下图中全等的图形
(4)判断下列说法是否正确:
①五角星都是全等形; ( ) ⑤周长相等的长方形是全等形;( )
②面积相等的三角形是全 ( ) ⑥周长相等的正方形是全等形;( )
③全等的两个图形面积相等;( ) ⑦全等的两个三角形的大小和形状完全相同;( )
④等边三角形是全等图形; ( ) ⑧全等的两个图形的对应边-对应角-周长,面积都相等。( )
2、(1)、拿出纸片,对折以后用剪刀剪出两个三角形,观察发现:这两个三角形能够 。因此,我们把 的两个三角形叫做全等三角形。
结合课本153页第一至三自然段,填写下列空白:两个三角形重合时, 叫做对应顶点, 叫做对应边, 叫做对应角;全等三角形的 相等, 相等。
(2)、阅读课本153-154页,观察图5-8,填写下列空白:△ABC与△XYZ全等,我们把它记作 ,读作 ,注意在记两个三角形全等时,通常把表示对应点的字母写在 ,比如,△ABC与△XYZ全等时,
对应边 = ; = ; = ;
对应角 = ; = ; = ;
那就是说对应点必须“对号入座”,不能错位。
3、下列图形中至少有两个三角形是全等的,请写出你找到的对应边、对应角。
挖掘教材:
4、例1:如图,已知△AFD≌△CEB,说明AD与BC的位置与大小关系。阅读下面的解答过程,请补充完整。
解:AD与BC平行且相等。
∵ △AFD≌△CEB (已知)
∴ AD=CB ( )
= (全等三角形对应角相等)
∴ AD∥BC (内错角相等,两直线平行)
例2:(1)已知△MNP≌△NMQ,MN = 8㎝,NP=7㎝,PM=6㎝,则MQ的长为( )
(A)8㎝, (B)7㎝, (C)6㎝, (D)5㎝
(2)如果△ABC≌△A′B′C′,并且∠B=50°, ∠A=70°,A′B′=10㎝,那么∠C′= ,AB= 。
反思小结:
5、你是怎样去寻找全等三角形的对应边与对应角的?
由于两个全等三角形的位置关系不同,可以根据具体情况,针对两个三角形的不同位置关系,总结出寻找对应边、对应角的规律:
(1)有公共边时, 一定是对应边;
(2)有公共角时, 一定是对应角;
(3)有对顶角时, 一定是对应角;
(4)两个全等三角形中一对最长的边(或最大的角),一对最短的边(或最小的角)一定是对应边(或对应角)。
达标检测:
6、如图△ABC≌△CDA,AB=CD,那么下列结论错误的是( )
A、∠DAC=∠BC A B、AC=CA
C、∠D=∠B D、CD= BD
7、如图,两三角形△ABC≌△ADE,∠EAC=30°,则∠BAD= 度。
8、如图,已知△ABD≌△ACD,点B、D、C在同一条直线上,∠BAC= 90°,求∠B的度数,判断AD与BC的位置关系,并说明理由。
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(12)
(11)
图3
C
D
B
A
A
B
图1
D
E
C
A
B
D
C
O
E
图2
图5
F
E
D
C
B
A
7题
D
B
A
C
E
8题
D
C
A
B
XX中学 XXX 审核人:XXX
【学习课题】 第7课时 全等三角形的概念和性质
【学习目标】 1、图形全等的相关概念及性质;
2、能说出什么叫全等三角形,知道如何表示两个三角形全等;
3、能找出全等三角形的对应元素;
4、能应用“全等三角形对应边相等、对应角相等”的性质解决问题。
【学习重点】全等三角形对应边相等、对应角相等的性质,并能进行简单的推理和计算。
【学习难点】熟练应用全等三角形的性质解决问题。
【学习过程】
学习准备: 1、阅读教材148—150,153—154; 2、纸张、剪刀
解读教材:
1、阅读课本148—150,
(1)图形全等的概念:
(2)图形全等的性质:
(3)找出下图中全等的图形
(4)判断下列说法是否正确:
①五角星都是全等形; ( ) ⑤周长相等的长方形是全等形;( )
②面积相等的三角形是全 ( ) ⑥周长相等的正方形是全等形;( )
③全等的两个图形面积相等;( ) ⑦全等的两个三角形的大小和形状完全相同;( )
④等边三角形是全等图形; ( ) ⑧全等的两个图形的对应边-对应角-周长,面积都相等。( )
2、(1)、拿出纸片,对折以后用剪刀剪出两个三角形,观察发现:这两个三角形能够 。因此,我们把 的两个三角形叫做全等三角形。
结合课本153页第一至三自然段,填写下列空白:两个三角形重合时, 叫做对应顶点, 叫做对应边, 叫做对应角;全等三角形的 相等, 相等。
(2)、阅读课本153-154页,观察图5-8,填写下列空白:△ABC与△XYZ全等,我们把它记作 ,读作 ,注意在记两个三角形全等时,通常把表示对应点的字母写在 ,比如,△ABC与△XYZ全等时,
对应边 = ; = ; = ;
对应角 = ; = ; = ;
那就是说对应点必须“对号入座”,不能错位。
3、下列图形中至少有两个三角形是全等的,请写出你找到的对应边、对应角。
挖掘教材:
4、例1:如图,已知△AFD≌△CEB,说明AD与BC的位置与大小关系。阅读下面的解答过程,请补充完整。
解:AD与BC平行且相等。
∵ △AFD≌△CEB (已知)
∴ AD=CB ( )
= (全等三角形对应角相等)
∴ AD∥BC (内错角相等,两直线平行)
例2:(1)已知△MNP≌△NMQ,MN = 8㎝,NP=7㎝,PM=6㎝,则MQ的长为( )
(A)8㎝, (B)7㎝, (C)6㎝, (D)5㎝
(2)如果△ABC≌△A′B′C′,并且∠B=50°, ∠A=70°,A′B′=10㎝,那么∠C′= ,AB= 。
反思小结:
5、你是怎样去寻找全等三角形的对应边与对应角的?
由于两个全等三角形的位置关系不同,可以根据具体情况,针对两个三角形的不同位置关系,总结出寻找对应边、对应角的规律:
(1)有公共边时, 一定是对应边;
(2)有公共角时, 一定是对应角;
(3)有对顶角时, 一定是对应角;
(4)两个全等三角形中一对最长的边(或最大的角),一对最短的边(或最小的角)一定是对应边(或对应角)。
达标检测:
6、如图△ABC≌△CDA,AB=CD,那么下列结论错误的是( )
A、∠DAC=∠BC A B、AC=CA
C、∠D=∠B D、CD= BD
7、如图,两三角形△ABC≌△ADE,∠EAC=30°,则∠BAD= 度。
8、如图,已知△ABD≌△ACD,点B、D、C在同一条直线上,∠BAC= 90°,求∠B的度数,判断AD与BC的位置关系,并说明理由。
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(12)
(11)
图3
C
D
B
A
A
B
图1
D
E
C
A
B
D
C
O
E
图2
图5
F
E
D
C
B
A
7题
D
B
A
C
E
8题
D
C
A
B
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
