第五章三角形第八课时探索三角形全等的条件一
文档属性
| 名称 | 第五章三角形第八课时探索三角形全等的条件一 |

|
|
| 格式 | zip | ||
| 文件大小 | 21.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 00:00:00 | ||
图片预览

文档简介
三角形
XX中学 XXX 审核人:XXX
【学习课题】:第8课时 探索三角形全等的条件(1)
【学习目标】:1. 经历探索三角形全等条件的过程,体会利用操作归纳获得数学结论。
2. 掌握“边边边”判定三角形全等,了解三角形的稳定性。
3. 在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。
【学习重点】:掌握“边边边”判定三角形全等
【学习难点】:用“边边边”判定三角形全等,进行有条理的思考并进行简单的推理。
【学习过程】:
一﹑学习准备:全等三角形的性质(如图)
1. 文字语言:全等三角形的 相等。
2. 符号语言:
3. 按要求用吹塑纸剪以下三角形:(要求剪的三角形美观大方,并将条件标在纸片上,每个小组准备一)
(1)号纸片:有一个角为30°,其他条件不限。
(2)号纸片:有一条边为10㎝,其他条件不限。
(3)号纸片:∠B=45度,∠C=45度,其他条件不限。
(4)号纸片:AB=10cm, BC=8cm,其他条件不限。
(5)号纸片:一角∠B=45度,一边BC=8cm,其他条件不限。
(6)号纸片:已知一个三角形的三个角分别为40°、60°、80°,其他条件不限。
(7)号纸片:已知一个三角形的三条边分别是6㎝、8㎝,10㎝,其他条件不限。
解读教材:
将同学们手上的纸片与同桌对比,看看发现了什么?
(1).只给出一个条件或两个条件时,都 使所画的三角形 。
(2).如果给出三个条件画三角形, 两个三角形________(一定,不一定)全等。
如(6)号纸片 ,(7)号纸片 。
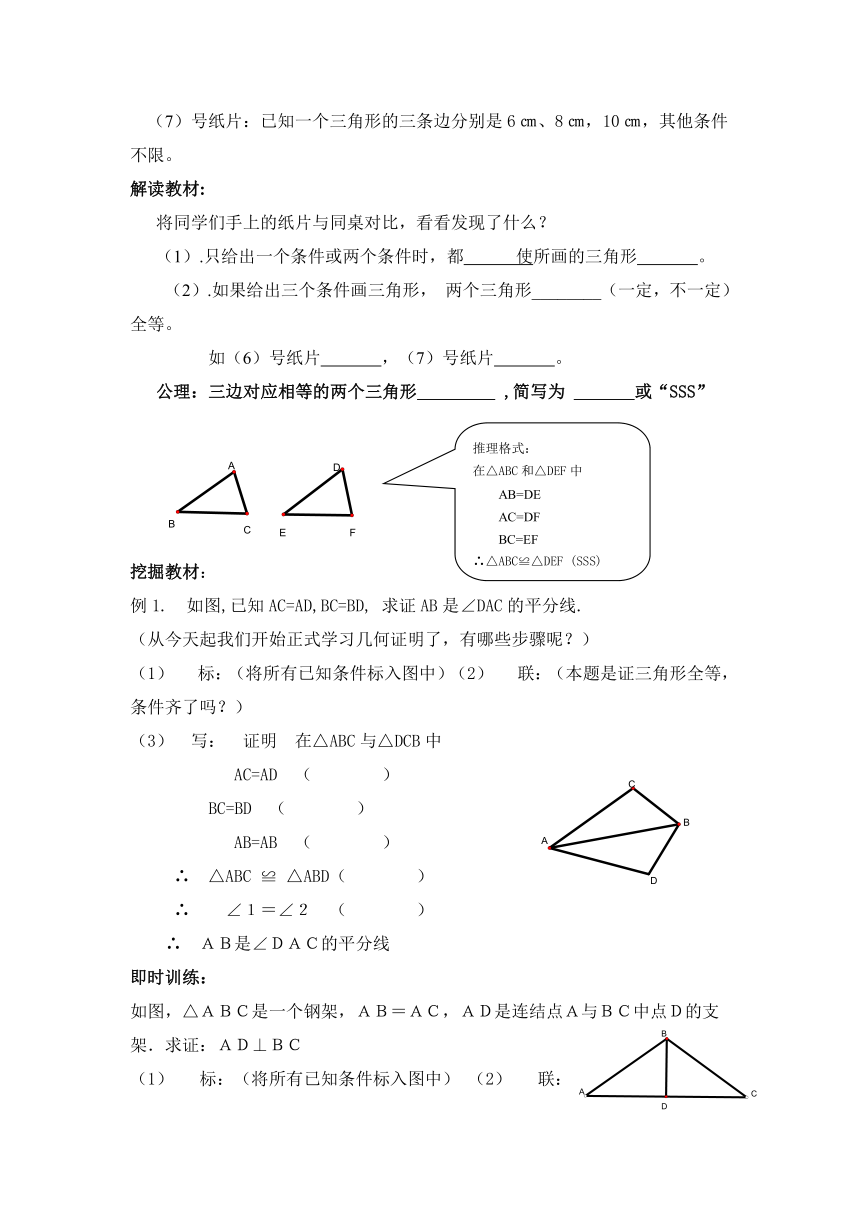
公理:三边对应相等的两个三角形 ,简写为 或“SSS”
挖掘教材:
例1. 如图,已知AC=AD,BC=BD, 求证AB是∠DAC的平分线. (从今天起我们开始正式学习几何证明了,有哪些步骤呢?)
(1) 标:(将所有已知条件标入图中)(2) 联:(本题是证三角形全等,条件齐了吗?)
(3) 写: 证明 在△ABC与△DCB中
AC=AD ( )
BC=BD ( )
AB=AB ( )
∴ △ABC ≌ △ABD( )
∴ ∠1=∠2 ( )
∴ AB是∠DAC的平分线
即时训练:
如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:AD⊥BC
(1) 标:(将所有已知条件标入图中) (2) 联:(本题全等的条件齐了吗?)
(3) 写: (完成本题需11项) (4) 证明:
性质运用
三角形的稳定性: 三角形的三边或三个顶点一旦确定,三角形的形状和大小就固定不变,这一性质叫三角形的 性,这一性质在生活和生产中有广泛应用,如 , 和 。而四边形的四边或四点确定时却没有这一性质,四边形的不稳定性在生活中也有应用,如伸缩门等。
反思小结:1.本节课在知识方面你有哪些收获? 2.这节课你积累了哪些数学活动经验?
达标测试:
1. 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?自选一组并说明理由.
(1) 标:(将所有已知条件标入图中) (2) 联:(全等的条件齐了吗?)
(3) 口述 :
2. 如图,四边形ABCD中,AB=CD,AD=BC,那么∠A=∠C吗?
(1) 标: (2) 联:
(3) 写:
3. 如图,AB=DE,AC=DF,BE=CF,△ABC与△DEF全等吗?你还能得出其他结论吗?
(1) 标: (2) 联:
(3) 写:
解题反思:解决线段或角的相等问题,经常要借全等三角形来解决。
我们知道:两个三角行全等,至少需要三个条件,而且至少要有一条边,还有哪几种情况呢
我们知道:两个三角行全等,至少需要三个条件,而且至少要有一条边,还有哪几种情况呢
推理格式:
∵△ABC≌△DEF
∴
推理格式:
在△ABC和△DEF中
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF (SSS)
XX中学 XXX 审核人:XXX
【学习课题】:第8课时 探索三角形全等的条件(1)
【学习目标】:1. 经历探索三角形全等条件的过程,体会利用操作归纳获得数学结论。
2. 掌握“边边边”判定三角形全等,了解三角形的稳定性。
3. 在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。
【学习重点】:掌握“边边边”判定三角形全等
【学习难点】:用“边边边”判定三角形全等,进行有条理的思考并进行简单的推理。
【学习过程】:
一﹑学习准备:全等三角形的性质(如图)
1. 文字语言:全等三角形的 相等。
2. 符号语言:
3. 按要求用吹塑纸剪以下三角形:(要求剪的三角形美观大方,并将条件标在纸片上,每个小组准备一)
(1)号纸片:有一个角为30°,其他条件不限。
(2)号纸片:有一条边为10㎝,其他条件不限。
(3)号纸片:∠B=45度,∠C=45度,其他条件不限。
(4)号纸片:AB=10cm, BC=8cm,其他条件不限。
(5)号纸片:一角∠B=45度,一边BC=8cm,其他条件不限。
(6)号纸片:已知一个三角形的三个角分别为40°、60°、80°,其他条件不限。
(7)号纸片:已知一个三角形的三条边分别是6㎝、8㎝,10㎝,其他条件不限。
解读教材:
将同学们手上的纸片与同桌对比,看看发现了什么?
(1).只给出一个条件或两个条件时,都 使所画的三角形 。
(2).如果给出三个条件画三角形, 两个三角形________(一定,不一定)全等。
如(6)号纸片 ,(7)号纸片 。
公理:三边对应相等的两个三角形 ,简写为 或“SSS”
挖掘教材:
例1. 如图,已知AC=AD,BC=BD, 求证AB是∠DAC的平分线. (从今天起我们开始正式学习几何证明了,有哪些步骤呢?)
(1) 标:(将所有已知条件标入图中)(2) 联:(本题是证三角形全等,条件齐了吗?)
(3) 写: 证明 在△ABC与△DCB中
AC=AD ( )
BC=BD ( )
AB=AB ( )
∴ △ABC ≌ △ABD( )
∴ ∠1=∠2 ( )
∴ AB是∠DAC的平分线
即时训练:
如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.求证:AD⊥BC
(1) 标:(将所有已知条件标入图中) (2) 联:(本题全等的条件齐了吗?)
(3) 写: (完成本题需11项) (4) 证明:
性质运用
三角形的稳定性: 三角形的三边或三个顶点一旦确定,三角形的形状和大小就固定不变,这一性质叫三角形的 性,这一性质在生活和生产中有广泛应用,如 , 和 。而四边形的四边或四点确定时却没有这一性质,四边形的不稳定性在生活中也有应用,如伸缩门等。
反思小结:1.本节课在知识方面你有哪些收获? 2.这节课你积累了哪些数学活动经验?
达标测试:
1. 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?自选一组并说明理由.
(1) 标:(将所有已知条件标入图中) (2) 联:(全等的条件齐了吗?)
(3) 口述 :
2. 如图,四边形ABCD中,AB=CD,AD=BC,那么∠A=∠C吗?
(1) 标: (2) 联:
(3) 写:
3. 如图,AB=DE,AC=DF,BE=CF,△ABC与△DEF全等吗?你还能得出其他结论吗?
(1) 标: (2) 联:
(3) 写:
解题反思:解决线段或角的相等问题,经常要借全等三角形来解决。
我们知道:两个三角行全等,至少需要三个条件,而且至少要有一条边,还有哪几种情况呢
我们知道:两个三角行全等,至少需要三个条件,而且至少要有一条边,还有哪几种情况呢
推理格式:
∵△ABC≌△DEF
∴
推理格式:
在△ABC和△DEF中
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF (SSS)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
