第五章三角形.第15,16课时回顾与思考
文档属性
| 名称 | 第五章三角形.第15,16课时回顾与思考 |  | |
| 格式 | zip | ||
| 文件大小 | 92.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-14 21:03:30 | ||
图片预览


文档简介
三角形
XX中学 XXX 审核人:XXX
【学习课题】 第15、16课时《三角形》梳理
【学习目标】
1.进一步认识三角形的有关概念,了解三边之间的关系以及三角形的内角和,了解三角形的稳定性。
2.经历探索三角形全等条件的过程,掌握两个三角形全等的条件,能应用三角形的全等解决一些实际问题。
3.能够用尺规作出三角形。
4.在复习过程中,通过观察、操作、想象、推理、交流等活动,发展空间观念,进一步积累数学活动经验,发展推理能力和有条理的表达能力。
【学习重点】三角形的基本性质和三角形全等的条件。
【学习难点】三角形全等的条件、应用及它的说理过程。
【学习过程】
一、学习准备:
㈠.工具准备:圆规、量角器、直尺、三角板等。
㈡.知识准备:
三角形的基本慨念
认识三角形 三边关系 三内角关系
三角形的高、中线、角平分线
三角形 图形的全等——慨念、特征、图案设计
三角形全等的基本慨念及特征
三角形全等 探索三角形全等的条件
直角三角形全等的条件
三角形全等的应用——尺规作图、解决实际问题
2.三角形全等的条件的选择问题
已知条件 可选择的方法
一边一角对应相等
两角对应相等
两边对应相等
对于直角三角形除了上述条件还有HL
在判定三角形全等时,应做到以下几点:
⑴根据已知条件与结论认真分析图形,将图形放进图形中。
⑵根据已知条件,确定对应元素,即找出相等的角或边。
⑶对照判断方法,看看还需什么条件两个三角形就全等。
⑷想办法找出所需的条件来:将间接条件转化为直接条件。
二、挖掘教材:(典型例析及课堂检测)
1.三角形相关概念:
例1:如图1,AB∥CD,AD,BC相交于O,∠BAD=35,∠BOD=76,则∠C的度数是______。
解:∵∠BOD=∠BAD+_____ ( )
∴_____=∠BOD-∠BAD=76-35=______ ( )
又∵AB∥CD ( )
∴_____=∠ABC=41 ( )
即时练习1:
⑴.在活动课上,小红已有两根长4cm,8cm的小木棒,现打算拼一个三角形,则小红应取的第三根小木棒的范围是______
⑵.若三角形的一个角是另一个角的6倍,而这两个角的和比第三个角大44,则此三角形的最大角是_______。
⑶.小明到工厂去进行社会实践,发现工人师傅生产了一种如图2所示的零件,工人
师傅告诉他:AB∥CD,∠A=40,∠1=70,小明马上运用已学的数学知识得出了∠C
的度数,聪明的你一定知道∠C=________。
2.全等三角形:
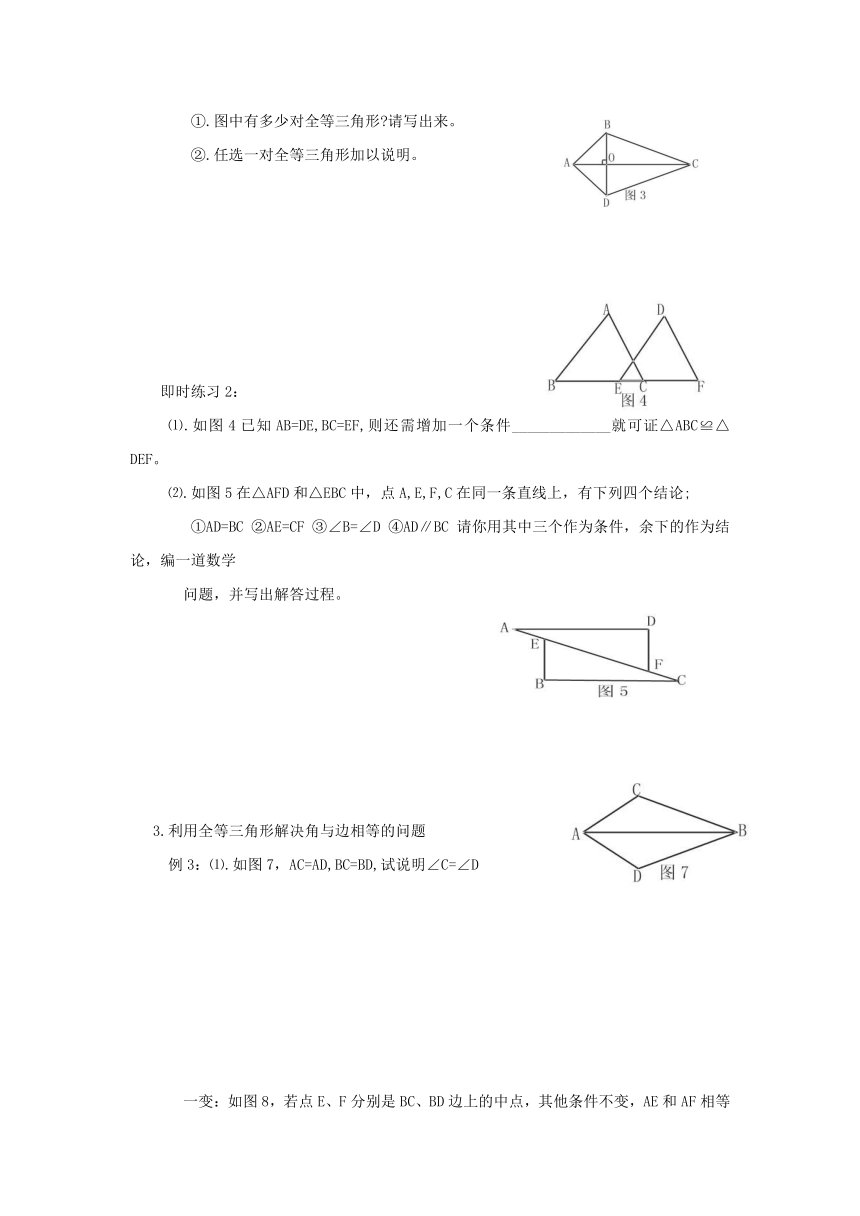
例2:如图3四边形ABCD中,AC⊥BD于点O,BO=DO。
①.图中有多少对全等三角形 请写出来。
②.任选一对全等三角形加以说明。
即时练习2:
⑴.如图4已知AB=DE,BC=EF,则还需增加一个条件_____________就可证△ABC≌△DEF。
⑵.如图5在△AFD和△EBC中,点A,E,F,C在同一条直线上,有下列四个结论;
①AD=BC ②AE=CF ③∠B=∠D ④AD∥BC 请你用其中三个作为条件,余下的作为结论,编一道数学
问题,并写出解答过程。
3.利用全等三角形解决角与边相等的问题
例3:⑴.如图7,AC=AD,BC=BD,试说明∠C=∠D
一变:如图8,若点E、F分别是BC、BD边上的中点,其他条件不变,AE和AF相等吗?
二变:如图9若连接CD,且CD与AB相交于点P,请你说明AB与CD有何关系?为什么?
即时练习3:
⑴.(一题多解)如图10,AD=AE,∠1=∠2,BD=CE,那么AB=AC是否成立?请说明理由。
⑵.如图11,点E在△ABC外部,点D在BC边上,DE交AC于F,若AC=AE,∠1=∠2=∠3,
试说明AB=AD
4.探究直角三角形全等
例4:如图12,AC=BD,AD⊥AC,BC⊥BD,那么AD与BC相等吗 说明理由。
一变:如图12-1,AD=BC,AD⊥AC,BC⊥BD,那么AC与BD相等吗 说明理由。
二变:如图12-2,DE⊥AC,CE⊥BD,EA=EB,试说明FD=FC。
即时练习4:
⑴.如图13,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E、F,试说明CE=DF。
⑵.如图14,△ABC中,∠ACB=90,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D,试说明:①.AE=CD;②.若AC=12cm,求BD的长。(提示:使用射影定理)
5.运用全等三角形测距离
例5:如图15,在一座楼相邻两面墙的外根部有两点A,C,请你设计方案测量A,C两点间的距离。
即时练习5:
⑴.某铁路施工队在建设铁路的过程中,需要打通一座小山,若图16,设计时需要测量隧道的长度,恰好在山的前面是一片空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖隧道的长度?请画出你设计的测量方案图并说明理由。
6.作图
⑴.已知三角形的两条边分别为3cm,4cm且3cm这条边所对的角是30求作这个三角形。
⑵.如图17,是举世闻名的三星堆考察发掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则对图中作哪些数据测量后,就可制作符合规格的三角形玉片模型,并说明其中理由。
三、归纳总结:
思想方法渗透:
1.分解图形法:复杂的图都是由简单的图形组成的,故可以将复杂的图形分解成几个基本图形,从而使问题简单化。
2.构造图形法:当直接说明线段、角相等,或三角形全等时有困难,常通过添加辅助线构造基本图形达到解题目的。
3.转化思想:转化思想就是将复杂问题转化为简单的问题,或将陌生的问题转化为熟悉的问题来处理的一种方法。
以上三种方法我们经常在解题中遇到,同学们在学习中总要遵循由特殊到一般的方法,不仅要学习逻辑推理,而且要合理推理一一猜想,不断培养自己的创新精神和实践能力。
XX中学 XXX 审核人:XXX
【学习课题】 第15、16课时《三角形》梳理
【学习目标】
1.进一步认识三角形的有关概念,了解三边之间的关系以及三角形的内角和,了解三角形的稳定性。
2.经历探索三角形全等条件的过程,掌握两个三角形全等的条件,能应用三角形的全等解决一些实际问题。
3.能够用尺规作出三角形。
4.在复习过程中,通过观察、操作、想象、推理、交流等活动,发展空间观念,进一步积累数学活动经验,发展推理能力和有条理的表达能力。
【学习重点】三角形的基本性质和三角形全等的条件。
【学习难点】三角形全等的条件、应用及它的说理过程。
【学习过程】
一、学习准备:
㈠.工具准备:圆规、量角器、直尺、三角板等。
㈡.知识准备:
三角形的基本慨念
认识三角形 三边关系 三内角关系
三角形的高、中线、角平分线
三角形 图形的全等——慨念、特征、图案设计
三角形全等的基本慨念及特征
三角形全等 探索三角形全等的条件
直角三角形全等的条件
三角形全等的应用——尺规作图、解决实际问题
2.三角形全等的条件的选择问题
已知条件 可选择的方法
一边一角对应相等
两角对应相等
两边对应相等
对于直角三角形除了上述条件还有HL
在判定三角形全等时,应做到以下几点:
⑴根据已知条件与结论认真分析图形,将图形放进图形中。
⑵根据已知条件,确定对应元素,即找出相等的角或边。
⑶对照判断方法,看看还需什么条件两个三角形就全等。
⑷想办法找出所需的条件来:将间接条件转化为直接条件。
二、挖掘教材:(典型例析及课堂检测)
1.三角形相关概念:
例1:如图1,AB∥CD,AD,BC相交于O,∠BAD=35,∠BOD=76,则∠C的度数是______。
解:∵∠BOD=∠BAD+_____ ( )
∴_____=∠BOD-∠BAD=76-35=______ ( )
又∵AB∥CD ( )
∴_____=∠ABC=41 ( )
即时练习1:
⑴.在活动课上,小红已有两根长4cm,8cm的小木棒,现打算拼一个三角形,则小红应取的第三根小木棒的范围是______
⑵.若三角形的一个角是另一个角的6倍,而这两个角的和比第三个角大44,则此三角形的最大角是_______。
⑶.小明到工厂去进行社会实践,发现工人师傅生产了一种如图2所示的零件,工人
师傅告诉他:AB∥CD,∠A=40,∠1=70,小明马上运用已学的数学知识得出了∠C
的度数,聪明的你一定知道∠C=________。
2.全等三角形:
例2:如图3四边形ABCD中,AC⊥BD于点O,BO=DO。
①.图中有多少对全等三角形 请写出来。
②.任选一对全等三角形加以说明。
即时练习2:
⑴.如图4已知AB=DE,BC=EF,则还需增加一个条件_____________就可证△ABC≌△DEF。
⑵.如图5在△AFD和△EBC中,点A,E,F,C在同一条直线上,有下列四个结论;
①AD=BC ②AE=CF ③∠B=∠D ④AD∥BC 请你用其中三个作为条件,余下的作为结论,编一道数学
问题,并写出解答过程。
3.利用全等三角形解决角与边相等的问题
例3:⑴.如图7,AC=AD,BC=BD,试说明∠C=∠D
一变:如图8,若点E、F分别是BC、BD边上的中点,其他条件不变,AE和AF相等吗?
二变:如图9若连接CD,且CD与AB相交于点P,请你说明AB与CD有何关系?为什么?
即时练习3:
⑴.(一题多解)如图10,AD=AE,∠1=∠2,BD=CE,那么AB=AC是否成立?请说明理由。
⑵.如图11,点E在△ABC外部,点D在BC边上,DE交AC于F,若AC=AE,∠1=∠2=∠3,
试说明AB=AD
4.探究直角三角形全等
例4:如图12,AC=BD,AD⊥AC,BC⊥BD,那么AD与BC相等吗 说明理由。
一变:如图12-1,AD=BC,AD⊥AC,BC⊥BD,那么AC与BD相等吗 说明理由。
二变:如图12-2,DE⊥AC,CE⊥BD,EA=EB,试说明FD=FC。
即时练习4:
⑴.如图13,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E、F,试说明CE=DF。
⑵.如图14,△ABC中,∠ACB=90,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D,试说明:①.AE=CD;②.若AC=12cm,求BD的长。(提示:使用射影定理)
5.运用全等三角形测距离
例5:如图15,在一座楼相邻两面墙的外根部有两点A,C,请你设计方案测量A,C两点间的距离。
即时练习5:
⑴.某铁路施工队在建设铁路的过程中,需要打通一座小山,若图16,设计时需要测量隧道的长度,恰好在山的前面是一片空地,利用这样的有利地形,测量人员是否可以利用三角形全等的知识测量出需要开挖隧道的长度?请画出你设计的测量方案图并说明理由。
6.作图
⑴.已知三角形的两条边分别为3cm,4cm且3cm这条边所对的角是30求作这个三角形。
⑵.如图17,是举世闻名的三星堆考察发掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则对图中作哪些数据测量后,就可制作符合规格的三角形玉片模型,并说明其中理由。
三、归纳总结:
思想方法渗透:
1.分解图形法:复杂的图都是由简单的图形组成的,故可以将复杂的图形分解成几个基本图形,从而使问题简单化。
2.构造图形法:当直接说明线段、角相等,或三角形全等时有困难,常通过添加辅助线构造基本图形达到解题目的。
3.转化思想:转化思想就是将复杂问题转化为简单的问题,或将陌生的问题转化为熟悉的问题来处理的一种方法。
以上三种方法我们经常在解题中遇到,同学们在学习中总要遵循由特殊到一般的方法,不仅要学习逻辑推理,而且要合理推理一一猜想,不断培养自己的创新精神和实践能力。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
