舒城县2010—2011学年度第一学期八年级数学期末质量检测
文档属性
| 名称 | 舒城县2010—2011学年度第一学期八年级数学期末质量检测 |  | |
| 格式 | zip | ||
| 文件大小 | 123.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-15 06:23:33 | ||
图片预览


文档简介
舒城县2010—2011学年度第一学期期末质量检测
八年级数学试卷
一、选择题(本题共10小题,每小题3分,计30分)
1.下列各组线段中,不能组成三角形的是( )
A.3、4、6 B.3、3、3 C.4、6、10 D.2、2、3
C
2.如图,,AB=6,OA=7,OB=8,则OC=( )
A.6 B.7 C.8 D.不能确定
B
3.观察下列银行标志,从图案看既是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
C
4.在平面直角坐标系内,把点P(-3,1)向右平移2个单位,则得到的对应点P′的坐标是( )
A. (-3,3) B.(-1,1) C.(-5,1) D.(-5,-1)
B
5.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A.8 B.7 C. 4 D.3
B
6.点Q(n+3,n-7)在轴上,则下列说法不正确的是( )
A .n=7 B.n=-3 C .Q点纵坐标为0 D.Q点横坐标为10
B
7.两直线的交点坐标( )
A.(—2,3) B.(2,—3) C.(—2,—3) D.(2,3)
D
8.如图 所示,AB = AC ,要说明△ADC≌△AEB,需添加的条件不能是( )
A.∠B =∠C B. AD = AE
C.∠ADC=∠AEB D. DC = BE
D
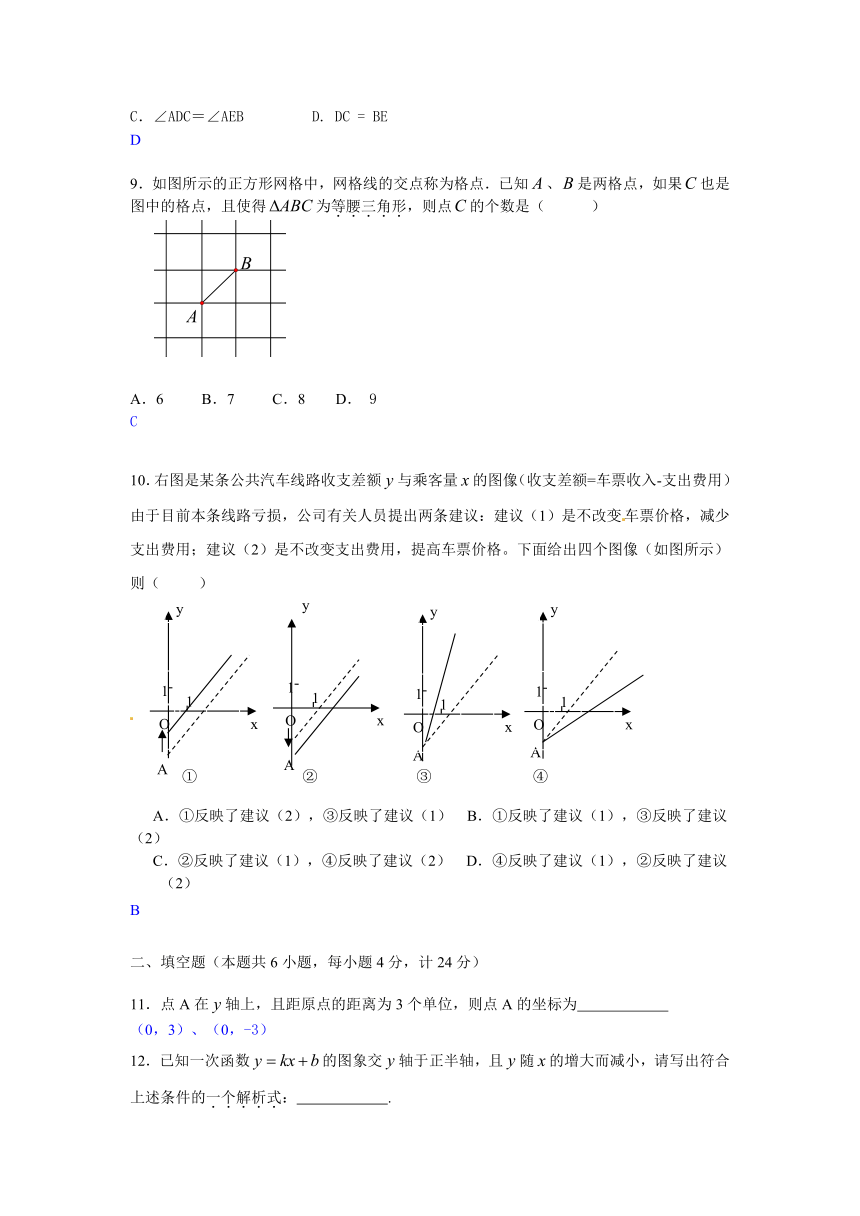
9.如图所示的正方形网格中,网格线的交点称为格点.已知、是两格点,如果也是图中的格点,且使得为等腰三角形,则点的个数是( )
A.6 B.7 C.8 D. 9
C
10.右图是某条公共汽车线路收支差额与乘客量的图像(收支差额=车票收入-支出费用)
由于目前本条线路亏损,公司有关人员提出两条建议:建议(1)是不改变车票价格,减少支出费用;建议(2)是不改变支出费用,提高车票价格。下面给出四个图像(如图所示)则( )
A.①反映了建议(2),③反映了建议(1) B.①反映了建议(1),③反映了建议(2)
C.②反映了建议(1),④反映了建议(2) D.④反映了建议(1),②反映了建议(2)
B
二、填空题(本题共6小题,每小题4分,计24分)
11.点A在轴上,且距原点的距离为3个单位,则点A的坐标为
(0,3)、(0,-3)
12.已知一次函数的图象交轴于正半轴,且随的增大而减小,请写出符合上述条件的一个解析式: .
如,(答案不惟一,且即可)
13.如图,BD是△ABC的角平分线,∠ABD=36°,∠C=72°,则图中的等腰三角形_____个.
3
14.如图,正六边形ABCDEF关于直线l的轴对称图形是六边形.下列判断错误的是 .
甲 AB= 乙 BC// 丙.直线l⊥ 丁
乙
15.如图,直线:与直线:相交于点P(,2),则关于的不等式≥的解集为 .
≥1
16.在直角坐标系中,已知ABC的三个顶点坐标分别为A(1,1)、B(3,1)、C(4,3),若要使ABD与ABC全等,则D点的坐标是 .
(0,-1)、(0,3)、(4,-1)
三、解答题(本题共小题,计66分)
17.(8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt △ABC的顶点均在格点上,在建立平面直角坐标系后,若点A的坐标为(-6,1).
(1)写出点B的坐标为 ,点C的坐标为 .
(2)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形,并写出点A1的坐标为 .
17.B(-3,1)、C(-3,3)、A1(-1,1)(一个空2分,图2分,计8分)
18.(8分)海拔高度每上升1千米,温度下降6℃.某时刻,万佛山地面温度为20℃,设高出地面千米处的温度为℃.
(1)写出与之间的函数关系式;
(2)已知万佛山某山峰高出地面约600米,求这时山顶的温度大约是多少℃?
⑴ () (5分,没有的得4分)
⑵ 600米=0.6千米 (℃) (3分,计8分)
19.(8分) 如图,点E、C在BF上,BE=FC,∠ABC=∠DEF,∠A=∠D=90°.
求证:AB=DE;
证明:∵BE=FC,∴BC=EF.(2分)
又∵∠ABC=∠DEF,∠A=∠D,(2分,计4分)
∴△ABC≌△DEF.(2分,计6分)
∴AB=DE.(2分,计8分)
20.(8分)已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使 CE = CD.求证:BD = DE.
∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,(2 分)
∵D为AC中点,∴∠DBC=30°(2分,计4分) ∵CE = CD,∴∠E=30°,
∴∠DBC=∠E,∴BD = DE.(4分,计8分)
21(10分).如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=30°,点B、C、D在直线上,画出点E关于直线的对称点E’,连接CE’ 、DE’ (保留画图痕迹),并求出
∠ACE’的度数.
21.画图(4 分,不写画法,只要图形准确,痕迹保留不扣分)
在△ABC中,∵AB=AC,∠BAC=30°∴∠ACB=75°(3分,计7分)
∵点E关于直线的对称点为E’ ∴∠E’CD=∠ECD=30°,∴∠ACE’=180°-∠ACB-
∠E’CD=75°(3分,计10分)
22.(12分)某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;(2)对的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
22.(1)设按优惠方法①购买需用元,按优惠方法②购买需用元
(2分)
. (2分,计4分)
(2)设,即,
.当整数时,选择优惠方法②.(2分,计6分)
设,∴当时,选择优惠方法①,②均可.
∴当整数时,选择优惠方法①.(2分,计8分)
(3)因为需要购买4个书包和12支水性笔,而,
购买方案一:用优惠方法①购买,需元;
购买方案二:采用两种购买方式,用优惠方法①购买4个书包,
需要=80元,同时获赠4支水性笔;
用优惠方法②购买8支水性笔,需要元.
共需80+36=116元.显然116<120.
最佳购买方案是:
用优惠方法①购买4个书包,获赠4支水性笔;再用优惠方法②购买8支水性笔.(分,计12分)
23(12分).如图,已知中,厘米,厘米,点为的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
解:(1)①∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
∴.(4分)
②∵, ∴,
又∵,,则,
∴点,点运动的时间秒,
∴厘米/秒.(4分,计8分)
(2)设经过秒后点与点第一次相遇,
由题意,得,
解得秒.
∴点共运动了厘米.
∵,
∴点、点在边上相遇,
∴经过秒点与点第一次在边上相遇. (4分,计12分)
A
C
D
B
O
F
y
A
1
1
x
y
O
A
1
1
x
y
O
A
1
1
x
y
O
1
1
x
O
A
②
①
③
]]\\
④
y
x
O
P
2
a
_
M
_
A
_
B
_
C
_
D
_
F
_
E
A
B
C
D
E
A
Q
C
D
B
P
A
Q
C
D
B
P
八年级数学试卷
一、选择题(本题共10小题,每小题3分,计30分)
1.下列各组线段中,不能组成三角形的是( )
A.3、4、6 B.3、3、3 C.4、6、10 D.2、2、3
C
2.如图,,AB=6,OA=7,OB=8,则OC=( )
A.6 B.7 C.8 D.不能确定
B
3.观察下列银行标志,从图案看既是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
C
4.在平面直角坐标系内,把点P(-3,1)向右平移2个单位,则得到的对应点P′的坐标是( )
A. (-3,3) B.(-1,1) C.(-5,1) D.(-5,-1)
B
5.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A.8 B.7 C. 4 D.3
B
6.点Q(n+3,n-7)在轴上,则下列说法不正确的是( )
A .n=7 B.n=-3 C .Q点纵坐标为0 D.Q点横坐标为10
B
7.两直线的交点坐标( )
A.(—2,3) B.(2,—3) C.(—2,—3) D.(2,3)
D
8.如图 所示,AB = AC ,要说明△ADC≌△AEB,需添加的条件不能是( )
A.∠B =∠C B. AD = AE
C.∠ADC=∠AEB D. DC = BE
D
9.如图所示的正方形网格中,网格线的交点称为格点.已知、是两格点,如果也是图中的格点,且使得为等腰三角形,则点的个数是( )
A.6 B.7 C.8 D. 9
C
10.右图是某条公共汽车线路收支差额与乘客量的图像(收支差额=车票收入-支出费用)
由于目前本条线路亏损,公司有关人员提出两条建议:建议(1)是不改变车票价格,减少支出费用;建议(2)是不改变支出费用,提高车票价格。下面给出四个图像(如图所示)则( )
A.①反映了建议(2),③反映了建议(1) B.①反映了建议(1),③反映了建议(2)
C.②反映了建议(1),④反映了建议(2) D.④反映了建议(1),②反映了建议(2)
B
二、填空题(本题共6小题,每小题4分,计24分)
11.点A在轴上,且距原点的距离为3个单位,则点A的坐标为
(0,3)、(0,-3)
12.已知一次函数的图象交轴于正半轴,且随的增大而减小,请写出符合上述条件的一个解析式: .
如,(答案不惟一,且即可)
13.如图,BD是△ABC的角平分线,∠ABD=36°,∠C=72°,则图中的等腰三角形_____个.
3
14.如图,正六边形ABCDEF关于直线l的轴对称图形是六边形.下列判断错误的是 .
甲 AB= 乙 BC// 丙.直线l⊥ 丁
乙
15.如图,直线:与直线:相交于点P(,2),则关于的不等式≥的解集为 .
≥1
16.在直角坐标系中,已知ABC的三个顶点坐标分别为A(1,1)、B(3,1)、C(4,3),若要使ABD与ABC全等,则D点的坐标是 .
(0,-1)、(0,3)、(4,-1)
三、解答题(本题共小题,计66分)
17.(8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt △ABC的顶点均在格点上,在建立平面直角坐标系后,若点A的坐标为(-6,1).
(1)写出点B的坐标为 ,点C的坐标为 .
(2)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形,并写出点A1的坐标为 .
17.B(-3,1)、C(-3,3)、A1(-1,1)(一个空2分,图2分,计8分)
18.(8分)海拔高度每上升1千米,温度下降6℃.某时刻,万佛山地面温度为20℃,设高出地面千米处的温度为℃.
(1)写出与之间的函数关系式;
(2)已知万佛山某山峰高出地面约600米,求这时山顶的温度大约是多少℃?
⑴ () (5分,没有的得4分)
⑵ 600米=0.6千米 (℃) (3分,计8分)
19.(8分) 如图,点E、C在BF上,BE=FC,∠ABC=∠DEF,∠A=∠D=90°.
求证:AB=DE;
证明:∵BE=FC,∴BC=EF.(2分)
又∵∠ABC=∠DEF,∠A=∠D,(2分,计4分)
∴△ABC≌△DEF.(2分,计6分)
∴AB=DE.(2分,计8分)
20.(8分)已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使 CE = CD.求证:BD = DE.
∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,(2 分)
∵D为AC中点,∴∠DBC=30°(2分,计4分) ∵CE = CD,∴∠E=30°,
∴∠DBC=∠E,∴BD = DE.(4分,计8分)
21(10分).如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=30°,点B、C、D在直线上,画出点E关于直线的对称点E’,连接CE’ 、DE’ (保留画图痕迹),并求出
∠ACE’的度数.
21.画图(4 分,不写画法,只要图形准确,痕迹保留不扣分)
在△ABC中,∵AB=AC,∠BAC=30°∴∠ACB=75°(3分,计7分)
∵点E关于直线的对称点为E’ ∴∠E’CD=∠ECD=30°,∴∠ACE’=180°-∠ACB-
∠E’CD=75°(3分,计10分)
22.(12分)某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;(2)对的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
22.(1)设按优惠方法①购买需用元,按优惠方法②购买需用元
(2分)
. (2分,计4分)
(2)设,即,
.当整数时,选择优惠方法②.(2分,计6分)
设,∴当时,选择优惠方法①,②均可.
∴当整数时,选择优惠方法①.(2分,计8分)
(3)因为需要购买4个书包和12支水性笔,而,
购买方案一:用优惠方法①购买,需元;
购买方案二:采用两种购买方式,用优惠方法①购买4个书包,
需要=80元,同时获赠4支水性笔;
用优惠方法②购买8支水性笔,需要元.
共需80+36=116元.显然116<120.
最佳购买方案是:
用优惠方法①购买4个书包,获赠4支水性笔;再用优惠方法②购买8支水性笔.(分,计12分)
23(12分).如图,已知中,厘米,厘米,点为的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
解:(1)①∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
∴.(4分)
②∵, ∴,
又∵,,则,
∴点,点运动的时间秒,
∴厘米/秒.(4分,计8分)
(2)设经过秒后点与点第一次相遇,
由题意,得,
解得秒.
∴点共运动了厘米.
∵,
∴点、点在边上相遇,
∴经过秒点与点第一次在边上相遇. (4分,计12分)
A
C
D
B
O
F
y
A
1
1
x
y
O
A
1
1
x
y
O
A
1
1
x
y
O
1
1
x
O
A
②
①
③
]]\\
④
y
x
O
P
2
a
_
M
_
A
_
B
_
C
_
D
_
F
_
E
A
B
C
D
E
A
Q
C
D
B
P
A
Q
C
D
B
P
同课章节目录
