2020-2021学年人教新版七年级数学上册《2.1 整式》 高频易错题集(附解析)
文档属性
| 名称 | 2020-2021学年人教新版七年级数学上册《2.1 整式》 高频易错题集(附解析) | 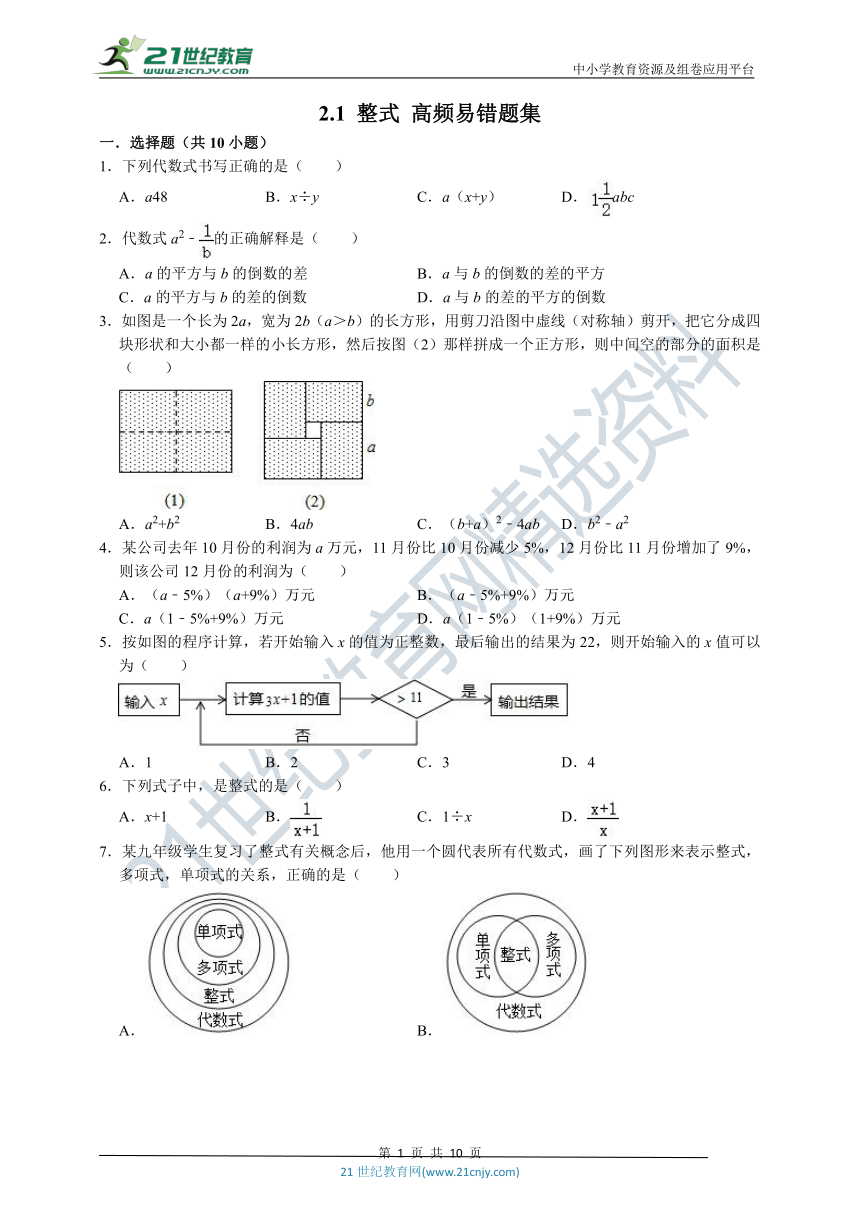 | |
| 格式 | zip | ||
| 文件大小 | 352.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 16:43:13 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
2.1
整式
高频易错题集
一.选择题(共10小题)
1.下列代数式书写正确的是( )
A.a48
B.x÷y
C.a(x+y)
D.abc
2.代数式a2﹣的正确解释是( )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
3.如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A.a2+b2
B.4ab
C.(b+a)2﹣4ab
D.b2﹣a2
4.某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A.(a﹣5%)(a+9%)万元
B.(a﹣5%+9%)万元
C.a(1﹣5%+9%)万元
D.a(1﹣5%)(1+9%)万元
5.按如图的程序计算,若开始输入x的值为正整数,最后输出的结果为22,则开始输入的x值可以为( )
A.1
B.2
C.3
D.4
6.下列式子中,是整式的是( )
A.x+1
B.
C.1÷x
D.
7.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
A.
B.
C.
D.
8.下列说法正确的是( )
A.的系数是﹣5
B.单项式x的系数为1,次数为0
C.xy+x﹣1是二次三项式
D.﹣22xyz2的次数是6
9.单项式的系数、次数分别是( )
A.﹣1,3
B.﹣3,2
C.,3
D.,2
10.下列各式:m,1,﹣xy2,x2+y2,其中单项式有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题)
11.代数式a×1应该写成
.
12.有一条铁丝长a米,用去了一半少b米(已知a>2b),则铁丝还剩
米.
13.已知关于x的代数式,当x=
时,代数式的最小值为
.
14.在代数式a,π,ab,a﹣b,,x2+x+1,5,2a,中,整式有
个;单项式有
个,次数为2的单项式是
;系数为1的单项式是
.
15.单项式﹣πxy2的次数是
.
三.解答题(共5小题)
16.请按代数式10x+30y编写一道与实际生活相关的应用题.
17.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.
(1)点B表示的数为
;
(2)若线段BM的长为4.5,则线段AC的长为
;
(3)若线段AC的长为x,求线段BM的长(用含x的式子表示).
18.甲、乙两家商场都以m(m>1000)元的价格购进了10台电器,每台销售定价都为n元.但在实际销售中,各自推出了优惠方案,甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.一段时间后,两家商场各自销售完了这10台电器,并且都有了盈利.
(1)如果销售完这10台电器,两家商场的盈利各多少元(结果用含m,n的式子表示)?
(2)如果销售完这10台电器,两家商场的盈利相差多少元(结果用含m,n的式子表示)?
(3)如果n=1700,那么某顾客想购买该种电器,应选择哪一家商场购买比较合算?说明理由.
19.写出所有系数是2,且含字母x及y的五次单项式.
20.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.
试题解析
一.选择题(共10小题)
1.下列代数式书写正确的是( )
A.a48
B.x÷y
C.a(x+y)
D.abc
【考点】代数式.
【分析】根据代数式的书写要求判断各项.
【解答】解:选项A正确的书写格式是48a,
B正确的书写格式是,
C正确,
D正确的书写格式是abc.
故选:C.
2.代数式a2﹣的正确解释是( )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
【考点】代数式.
【分析】根据代数式的字母表示,用文字解释代数式的意义即可.
【解答】解:因为代数式a2﹣计算过程是先算乘方,再算减法,
所以代数式a2﹣的正确解释是:
a的平方与b的倒数的差.
故选:A.
3.如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A.a2+b2
B.4ab
C.(b+a)2﹣4ab
D.b2﹣a2
【考点】列代数式.
【分析】先求出正方形的边长,继而得出面积,然后根据空白部分的面积=正方形的面积﹣矩形的面积即可得出答案.
【解答】解:∵图(1)是一个长为2a,宽为2b(a>b)的长方形,
∴正方形的边长为:a+b,
∵由题意可得,正方形的边长为(a+b),
正方形的面积为(a+b)2,
∵原矩形的面积为4ab,
∴中间空的部分的面积=(a+b)2﹣4ab.
故选:C.
4.某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A.(a﹣5%)(a+9%)万元
B.(a﹣5%+9%)万元
C.a(1﹣5%+9%)万元
D.a(1﹣5%)(1+9%)万元
【考点】列代数式.
【分析】先表示11月份利润为a(1﹣5%)万元,则12月份利润为a(1﹣5%)(1+9%)万元.
【解答】解:由题意得:12月份的利润为:a(1﹣5%)(1+9%)万元,
故选:D.
5.按如图的程序计算,若开始输入x的值为正整数,最后输出的结果为22,则开始输入的x值可以为( )
A.1
B.2
C.3
D.4
【考点】有理数的混合运算;代数式求值.
【分析】由3x+1=22,解得x=7,即开始输入的x为7,最后输出的结果为22;当开始输入的x值满足3x+1=7,最后输出的结果也为22,可解得x=2,符合题意.
【解答】解:当输入一个正整数,一次输出22时,
3x+1=22,
解得:x=7;
当输入一个正整数,两次后输出22时,
3x+1=7,
解得:x=2,
故选:B.
6.下列式子中,是整式的是( )
A.x+1
B.
C.1÷x
D.
【考点】整式.
【分析】根据整式的概念判断即可.
【解答】解:A、x+1是整式;
B、,分母中含有字母,不属于整式;
C、1÷x,分母中含有字母,不属于整式;
D、,分母中含有字母,不属于整式;
故选:A.
7.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
A.
B.
C.
D.
【考点】整式.
【分析】根据单项式、多项式、整式、分式、代数式的概念,作出判断.
【解答】解:代数式包括整式和分式,整式包括多项式和单项式,故正确的是选项D,
故选:D.
8.下列说法正确的是( )
A.的系数是﹣5
B.单项式x的系数为1,次数为0
C.xy+x﹣1是二次三项式
D.﹣22xyz2的次数是6
【考点】单项式;多项式.
【分析】根据单项式的系数、次数,可判断A、B、D,根据多项式的表示,可判断C,可得答案.
【解答】解:A的系数是﹣,故A错误;
B单项式x的系数为1,次数为1,故
B错误;
C
xy+x﹣1是二次三项式,故C正确;
D﹣22xyz2的次数是4,故D错误;
故选:C.
9.单项式的系数、次数分别是( )
A.﹣1,3
B.﹣3,2
C.,3
D.,2
【考点】单项式.
【分析】根据单项式系数及次数的定义进行解答即可.
【解答】解:单项式的系数为,次数为3.
故选:C.
10.下列各式:m,1,﹣xy2,x2+y2,其中单项式有( )
A.1个
B.2个
C.3个
D.4个
【考点】单项式;多项式.
【分析】根据单项式的定义进行解答即可.
【解答】解:m,1,﹣xy2是单项式;
x2+y2是多项式.
故选:C.
二.填空题(共5小题)
11.代数式a×1应该写成 .
【考点】代数式.
【分析】直接利用代数式书写方法分析得出答案.
【解答】解:a×1应该写成,
故答案为:.
12.有一条铁丝长a米,用去了一半少b米(已知a>2b),则铁丝还剩 (a+b) 米.
【考点】列代数式.
【分析】用铁丝的长减去用掉的铁丝的长度,即可得到剩余的铁丝的长度.
【解答】解:由题可得,铁丝还剩a﹣(a﹣b)=a+b(米),
故答案为:(a+b).
13.已知关于x的代数式,当x= 1或﹣1 时,代数式的最小值为 2 .
【考点】代数式求值.
【分析】根据a+b≥2,当a=b时取最小值,所以当x2=时,≥2取最小值2.
【解答】解:≥2=2,即≥2
所以当x2=时,代数式的最小值为2.
此时x=1或﹣1.
故答案为1或﹣1,2.
14.在代数式a,π,ab,a﹣b,,x2+x+1,5,2a,中,整式有 8 个;单项式有 5 个,次数为2的单项式是 ab ;系数为1的单项式是 a .
【考点】整式.
【分析】解决本题关键是搞清整式、单项式、多项式的概念,紧扣概念作出判断.
【解答】解:整式有a,π,ab,a﹣b,,x2+x+1,5,2a,共8个;
单项式有a,π,ab,5,2a共5个,次数为2的单项式是ab;
系数为1的单项式是a.
故答案为:8;5;ab;a.
15.单项式﹣πxy2的次数是 3 .
【考点】单项式.
【分析】单项式的次数是指所有字母的指数和,即1+2=3.
【解答】解:根据单项式的次数和系数的定义,单项式﹣πxy2的次数是3.
故答案为:3.
三.解答题(共5小题)
16.请按代数式10x+30y编写一道与实际生活相关的应用题.
【考点】代数式.
【分析】结合实际情境作答,答案不唯一.
【解答】解:答案不唯一.
如一个苹果的质量是x,一个桔子的质量是y,那么10个苹果和30个桔子的质量和是10x+30y.
17.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.
(1)点B表示的数为 ﹣1 ;
(2)若线段BM的长为4.5,则线段AC的长为 2或16 ;
(3)若线段AC的长为x,求线段BM的长(用含x的式子表示).
【考点】数轴;列代数式.
【分析】(1)根据点A表示的数为5,线段AB的长为线段OA长的1.2倍.即可得点B表示的数;
(2)根据线段BM的长为4.5,即可得线段AC的长;
(3)根据数轴,结合(2)的过程即可用含x的式子表示BM的长.
【解答】解:(1)∵点A表示的数为5,线段AB的长为线段OA长的1.2倍,
∴AB=1.2×5×=×6
∵OA=5,
∴OB=AB﹣OA=1,
∴点B表示的数为﹣1.
故答案为﹣1;
(2)∵BM=4.5,
∴OM=4.5﹣1=3.5(点M在原点右侧)
或OM=|﹣1﹣4.5|=5.5(点M在原点左侧)
∵M为线段OC的中点
∴OC=2OM=7或11
∴AC=7﹣5=2(点C在原点右侧)
或AC=11+5=16(点C在原点左侧)
∴线段AC的长为2或16.
故答案为2或16;
(3)当AC=x,
点C在点A右侧,OC=5+x
∴OM=OC=(5+x)
∴BM=OB+OM=1+(5+x)=x+
点C在线段OA上,OC=OA﹣AC=5﹣x
∴OM=OC=(5﹣x)
∴BM=OM﹣OB=(5﹣x)+1=﹣x+.
当点C在线段OB上时,OC=x﹣5,OM=(x﹣5),
BM=1﹣(x﹣5)=﹣x,
当点C在点B的左侧时,OC=x﹣5,OM=(x﹣5),BM=|1﹣(x﹣5)|=﹣x或x﹣,
答:线段BM的长为:x+或x﹣或﹣x.
18.甲、乙两家商场都以m(m>1000)元的价格购进了10台电器,每台销售定价都为n元.但在实际销售中,各自推出了优惠方案,甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.一段时间后,两家商场各自销售完了这10台电器,并且都有了盈利.
(1)如果销售完这10台电器,两家商场的盈利各多少元(结果用含m,n的式子表示)?
(2)如果销售完这10台电器,两家商场的盈利相差多少元(结果用含m,n的式子表示)?
(3)如果n=1700,那么某顾客想购买该种电器,应选择哪一家商场购买比较合算?说明理由.
【考点】列代数式;代数式求值.
【分析】(1)先求两个商场的买一台电器的费用,再用销售费用减去进价就是一台的利润,进而求出销售完10台的盈利;
(2)根据(1)中结论所得代数式相减即可;
(3)把n=1700代入(1)中销售费用代数式,即可选择比较合算的商场.
【解答】解:(1)根据题意,得
当n>1000时,
在甲商场的费用是:
1000+(n﹣1000)×90%=0.9n+100,
∴销售完这10台电器,甲家商场的盈利是:
10(0.9n+100﹣m)=(9n﹣10m+1000)元,
在乙商场的费用是:
500+(n﹣500)×95%=0.95n+25,
∴销售完这10台电器,乙家商场的盈利是:
10(0.95n+25﹣m)=(9.5n﹣10m+250)元.
答:销售完这10台电器,两家商场的盈利各(9n﹣10m+1000)元、(9.5n﹣10m+250)元.
(2)销售完这10台电器,两家商场的盈利相差:
|(9.5n﹣10m+250)﹣(9n﹣10m+1000)|
=|9.5n﹣10m+250﹣9n+10m﹣1000|
=|0.5n﹣750|
当n>1500时,相差(0.5n﹣750)元;
当1000<n≤1500时,相差(750﹣0.5n)元.
答:销售完这10台电器,两家商场的盈利相差:|0.5n﹣750|元.
(3)把n=1700代入(1)中的两个代数式:
0.9n+100=0.9×1700+100=1630,
0.95n+25=0.95×1700+25=1640,
∵1640>1630,
答:选择甲商场合算.
19.写出所有系数是2,且含字母x及y的五次单项式.
【考点】单项式.
【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
【解答】解:先构造系数为2,即数字因数为2,然后使x、y的指数和是5即可.
则满足题意的所有五次单项式有:2xy4、2x2y3、2x3y2、2x4y.
20.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.
【考点】多项式.
【分析】利用二次三项式的定义求解即可.
【解答】解:若(a﹣1)x2+x|a+2|﹣2x+b是二次三项式,
可得a=﹣1,b≠0或a=﹣3,b≠0或a=﹣2,b≠﹣1或a=﹣4,b≠0,
所以当a=﹣1,b≠0或a=﹣3,b≠0或a=﹣4,b≠0或a=﹣2,b≠﹣1.得(a﹣1)x2+x|a+2|﹣2x+b为二次三项式.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2.1
整式
高频易错题集
一.选择题(共10小题)
1.下列代数式书写正确的是( )
A.a48
B.x÷y
C.a(x+y)
D.abc
2.代数式a2﹣的正确解释是( )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
3.如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A.a2+b2
B.4ab
C.(b+a)2﹣4ab
D.b2﹣a2
4.某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A.(a﹣5%)(a+9%)万元
B.(a﹣5%+9%)万元
C.a(1﹣5%+9%)万元
D.a(1﹣5%)(1+9%)万元
5.按如图的程序计算,若开始输入x的值为正整数,最后输出的结果为22,则开始输入的x值可以为( )
A.1
B.2
C.3
D.4
6.下列式子中,是整式的是( )
A.x+1
B.
C.1÷x
D.
7.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
A.
B.
C.
D.
8.下列说法正确的是( )
A.的系数是﹣5
B.单项式x的系数为1,次数为0
C.xy+x﹣1是二次三项式
D.﹣22xyz2的次数是6
9.单项式的系数、次数分别是( )
A.﹣1,3
B.﹣3,2
C.,3
D.,2
10.下列各式:m,1,﹣xy2,x2+y2,其中单项式有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题)
11.代数式a×1应该写成
.
12.有一条铁丝长a米,用去了一半少b米(已知a>2b),则铁丝还剩
米.
13.已知关于x的代数式,当x=
时,代数式的最小值为
.
14.在代数式a,π,ab,a﹣b,,x2+x+1,5,2a,中,整式有
个;单项式有
个,次数为2的单项式是
;系数为1的单项式是
.
15.单项式﹣πxy2的次数是
.
三.解答题(共5小题)
16.请按代数式10x+30y编写一道与实际生活相关的应用题.
17.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.
(1)点B表示的数为
;
(2)若线段BM的长为4.5,则线段AC的长为
;
(3)若线段AC的长为x,求线段BM的长(用含x的式子表示).
18.甲、乙两家商场都以m(m>1000)元的价格购进了10台电器,每台销售定价都为n元.但在实际销售中,各自推出了优惠方案,甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.一段时间后,两家商场各自销售完了这10台电器,并且都有了盈利.
(1)如果销售完这10台电器,两家商场的盈利各多少元(结果用含m,n的式子表示)?
(2)如果销售完这10台电器,两家商场的盈利相差多少元(结果用含m,n的式子表示)?
(3)如果n=1700,那么某顾客想购买该种电器,应选择哪一家商场购买比较合算?说明理由.
19.写出所有系数是2,且含字母x及y的五次单项式.
20.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.
试题解析
一.选择题(共10小题)
1.下列代数式书写正确的是( )
A.a48
B.x÷y
C.a(x+y)
D.abc
【考点】代数式.
【分析】根据代数式的书写要求判断各项.
【解答】解:选项A正确的书写格式是48a,
B正确的书写格式是,
C正确,
D正确的书写格式是abc.
故选:C.
2.代数式a2﹣的正确解释是( )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
【考点】代数式.
【分析】根据代数式的字母表示,用文字解释代数式的意义即可.
【解答】解:因为代数式a2﹣计算过程是先算乘方,再算减法,
所以代数式a2﹣的正确解释是:
a的平方与b的倒数的差.
故选:A.
3.如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A.a2+b2
B.4ab
C.(b+a)2﹣4ab
D.b2﹣a2
【考点】列代数式.
【分析】先求出正方形的边长,继而得出面积,然后根据空白部分的面积=正方形的面积﹣矩形的面积即可得出答案.
【解答】解:∵图(1)是一个长为2a,宽为2b(a>b)的长方形,
∴正方形的边长为:a+b,
∵由题意可得,正方形的边长为(a+b),
正方形的面积为(a+b)2,
∵原矩形的面积为4ab,
∴中间空的部分的面积=(a+b)2﹣4ab.
故选:C.
4.某公司去年10月份的利润为a万元,11月份比10月份减少5%,12月份比11月份增加了9%,则该公司12月份的利润为( )
A.(a﹣5%)(a+9%)万元
B.(a﹣5%+9%)万元
C.a(1﹣5%+9%)万元
D.a(1﹣5%)(1+9%)万元
【考点】列代数式.
【分析】先表示11月份利润为a(1﹣5%)万元,则12月份利润为a(1﹣5%)(1+9%)万元.
【解答】解:由题意得:12月份的利润为:a(1﹣5%)(1+9%)万元,
故选:D.
5.按如图的程序计算,若开始输入x的值为正整数,最后输出的结果为22,则开始输入的x值可以为( )
A.1
B.2
C.3
D.4
【考点】有理数的混合运算;代数式求值.
【分析】由3x+1=22,解得x=7,即开始输入的x为7,最后输出的结果为22;当开始输入的x值满足3x+1=7,最后输出的结果也为22,可解得x=2,符合题意.
【解答】解:当输入一个正整数,一次输出22时,
3x+1=22,
解得:x=7;
当输入一个正整数,两次后输出22时,
3x+1=7,
解得:x=2,
故选:B.
6.下列式子中,是整式的是( )
A.x+1
B.
C.1÷x
D.
【考点】整式.
【分析】根据整式的概念判断即可.
【解答】解:A、x+1是整式;
B、,分母中含有字母,不属于整式;
C、1÷x,分母中含有字母,不属于整式;
D、,分母中含有字母,不属于整式;
故选:A.
7.某九年级学生复习了整式有关概念后,他用一个圆代表所有代数式,画了下列图形来表示整式,多项式,单项式的关系,正确的是( )
A.
B.
C.
D.
【考点】整式.
【分析】根据单项式、多项式、整式、分式、代数式的概念,作出判断.
【解答】解:代数式包括整式和分式,整式包括多项式和单项式,故正确的是选项D,
故选:D.
8.下列说法正确的是( )
A.的系数是﹣5
B.单项式x的系数为1,次数为0
C.xy+x﹣1是二次三项式
D.﹣22xyz2的次数是6
【考点】单项式;多项式.
【分析】根据单项式的系数、次数,可判断A、B、D,根据多项式的表示,可判断C,可得答案.
【解答】解:A的系数是﹣,故A错误;
B单项式x的系数为1,次数为1,故
B错误;
C
xy+x﹣1是二次三项式,故C正确;
D﹣22xyz2的次数是4,故D错误;
故选:C.
9.单项式的系数、次数分别是( )
A.﹣1,3
B.﹣3,2
C.,3
D.,2
【考点】单项式.
【分析】根据单项式系数及次数的定义进行解答即可.
【解答】解:单项式的系数为,次数为3.
故选:C.
10.下列各式:m,1,﹣xy2,x2+y2,其中单项式有( )
A.1个
B.2个
C.3个
D.4个
【考点】单项式;多项式.
【分析】根据单项式的定义进行解答即可.
【解答】解:m,1,﹣xy2是单项式;
x2+y2是多项式.
故选:C.
二.填空题(共5小题)
11.代数式a×1应该写成 .
【考点】代数式.
【分析】直接利用代数式书写方法分析得出答案.
【解答】解:a×1应该写成,
故答案为:.
12.有一条铁丝长a米,用去了一半少b米(已知a>2b),则铁丝还剩 (a+b) 米.
【考点】列代数式.
【分析】用铁丝的长减去用掉的铁丝的长度,即可得到剩余的铁丝的长度.
【解答】解:由题可得,铁丝还剩a﹣(a﹣b)=a+b(米),
故答案为:(a+b).
13.已知关于x的代数式,当x= 1或﹣1 时,代数式的最小值为 2 .
【考点】代数式求值.
【分析】根据a+b≥2,当a=b时取最小值,所以当x2=时,≥2取最小值2.
【解答】解:≥2=2,即≥2
所以当x2=时,代数式的最小值为2.
此时x=1或﹣1.
故答案为1或﹣1,2.
14.在代数式a,π,ab,a﹣b,,x2+x+1,5,2a,中,整式有 8 个;单项式有 5 个,次数为2的单项式是 ab ;系数为1的单项式是 a .
【考点】整式.
【分析】解决本题关键是搞清整式、单项式、多项式的概念,紧扣概念作出判断.
【解答】解:整式有a,π,ab,a﹣b,,x2+x+1,5,2a,共8个;
单项式有a,π,ab,5,2a共5个,次数为2的单项式是ab;
系数为1的单项式是a.
故答案为:8;5;ab;a.
15.单项式﹣πxy2的次数是 3 .
【考点】单项式.
【分析】单项式的次数是指所有字母的指数和,即1+2=3.
【解答】解:根据单项式的次数和系数的定义,单项式﹣πxy2的次数是3.
故答案为:3.
三.解答题(共5小题)
16.请按代数式10x+30y编写一道与实际生活相关的应用题.
【考点】代数式.
【分析】结合实际情境作答,答案不唯一.
【解答】解:答案不唯一.
如一个苹果的质量是x,一个桔子的质量是y,那么10个苹果和30个桔子的质量和是10x+30y.
17.点O为数轴的原点,点A、B在数轴上的位置如图所示,点A表示的数为5,线段AB的长为线段OA长的1.2倍.点C在数轴上,M为线段OC的中点.
(1)点B表示的数为 ﹣1 ;
(2)若线段BM的长为4.5,则线段AC的长为 2或16 ;
(3)若线段AC的长为x,求线段BM的长(用含x的式子表示).
【考点】数轴;列代数式.
【分析】(1)根据点A表示的数为5,线段AB的长为线段OA长的1.2倍.即可得点B表示的数;
(2)根据线段BM的长为4.5,即可得线段AC的长;
(3)根据数轴,结合(2)的过程即可用含x的式子表示BM的长.
【解答】解:(1)∵点A表示的数为5,线段AB的长为线段OA长的1.2倍,
∴AB=1.2×5×=×6
∵OA=5,
∴OB=AB﹣OA=1,
∴点B表示的数为﹣1.
故答案为﹣1;
(2)∵BM=4.5,
∴OM=4.5﹣1=3.5(点M在原点右侧)
或OM=|﹣1﹣4.5|=5.5(点M在原点左侧)
∵M为线段OC的中点
∴OC=2OM=7或11
∴AC=7﹣5=2(点C在原点右侧)
或AC=11+5=16(点C在原点左侧)
∴线段AC的长为2或16.
故答案为2或16;
(3)当AC=x,
点C在点A右侧,OC=5+x
∴OM=OC=(5+x)
∴BM=OB+OM=1+(5+x)=x+
点C在线段OA上,OC=OA﹣AC=5﹣x
∴OM=OC=(5﹣x)
∴BM=OM﹣OB=(5﹣x)+1=﹣x+.
当点C在线段OB上时,OC=x﹣5,OM=(x﹣5),
BM=1﹣(x﹣5)=﹣x,
当点C在点B的左侧时,OC=x﹣5,OM=(x﹣5),BM=|1﹣(x﹣5)|=﹣x或x﹣,
答:线段BM的长为:x+或x﹣或﹣x.
18.甲、乙两家商场都以m(m>1000)元的价格购进了10台电器,每台销售定价都为n元.但在实际销售中,各自推出了优惠方案,甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.一段时间后,两家商场各自销售完了这10台电器,并且都有了盈利.
(1)如果销售完这10台电器,两家商场的盈利各多少元(结果用含m,n的式子表示)?
(2)如果销售完这10台电器,两家商场的盈利相差多少元(结果用含m,n的式子表示)?
(3)如果n=1700,那么某顾客想购买该种电器,应选择哪一家商场购买比较合算?说明理由.
【考点】列代数式;代数式求值.
【分析】(1)先求两个商场的买一台电器的费用,再用销售费用减去进价就是一台的利润,进而求出销售完10台的盈利;
(2)根据(1)中结论所得代数式相减即可;
(3)把n=1700代入(1)中销售费用代数式,即可选择比较合算的商场.
【解答】解:(1)根据题意,得
当n>1000时,
在甲商场的费用是:
1000+(n﹣1000)×90%=0.9n+100,
∴销售完这10台电器,甲家商场的盈利是:
10(0.9n+100﹣m)=(9n﹣10m+1000)元,
在乙商场的费用是:
500+(n﹣500)×95%=0.95n+25,
∴销售完这10台电器,乙家商场的盈利是:
10(0.95n+25﹣m)=(9.5n﹣10m+250)元.
答:销售完这10台电器,两家商场的盈利各(9n﹣10m+1000)元、(9.5n﹣10m+250)元.
(2)销售完这10台电器,两家商场的盈利相差:
|(9.5n﹣10m+250)﹣(9n﹣10m+1000)|
=|9.5n﹣10m+250﹣9n+10m﹣1000|
=|0.5n﹣750|
当n>1500时,相差(0.5n﹣750)元;
当1000<n≤1500时,相差(750﹣0.5n)元.
答:销售完这10台电器,两家商场的盈利相差:|0.5n﹣750|元.
(3)把n=1700代入(1)中的两个代数式:
0.9n+100=0.9×1700+100=1630,
0.95n+25=0.95×1700+25=1640,
∵1640>1630,
答:选择甲商场合算.
19.写出所有系数是2,且含字母x及y的五次单项式.
【考点】单项式.
【分析】根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
【解答】解:先构造系数为2,即数字因数为2,然后使x、y的指数和是5即可.
则满足题意的所有五次单项式有:2xy4、2x2y3、2x3y2、2x4y.
20.已知关于x的多项式(a﹣1)x2+x|a+2|﹣2x+b,问是否存在实数a,b,使得这个多项式为二次三项式?若存在,请求出a,b的值,若不存在,请说明理由.
【考点】多项式.
【分析】利用二次三项式的定义求解即可.
【解答】解:若(a﹣1)x2+x|a+2|﹣2x+b是二次三项式,
可得a=﹣1,b≠0或a=﹣3,b≠0或a=﹣2,b≠﹣1或a=﹣4,b≠0,
所以当a=﹣1,b≠0或a=﹣3,b≠0或a=﹣4,b≠0或a=﹣2,b≠﹣1.得(a﹣1)x2+x|a+2|﹣2x+b为二次三项式.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
