3.3相似三角形的判定2

(共11张PPT)
我们现在判定两个三角形是否相似，必须要知道它们的对应角是否相等，对应边是否成比例．那么是否存在判定两个三角形相似的简便方法呢？
观察你与你同伴的直角三角尺，同样角度（30°与60°，或45°与45°）的三角尺看起来是相似的．这样从直观来看，一个三角形的三个角分别与另一个三角形的三个角对应相等时，它们就“应该”相似了.确实这样吗？
我们在判断两个三角形全等时，使用了哪些方法？判断三角形相似是否有类似的方法呢？
如果一个三角形的三个角分别与另一个三角形的三个角对应相等，那么它们相似吗？
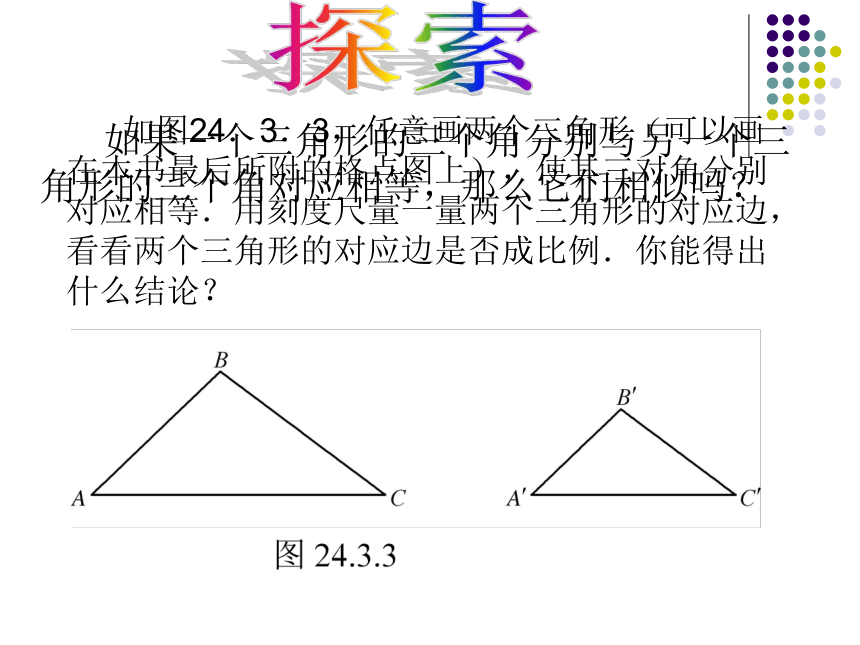
如图24．3．3，任意画两个三角形（可以画在本书最后所附的格点图上），使其三对角分别对应相等．用刻度尺量一量两个三角形的对应边，看看两个三角形的对应边是否成比例．你能得出什么结论？
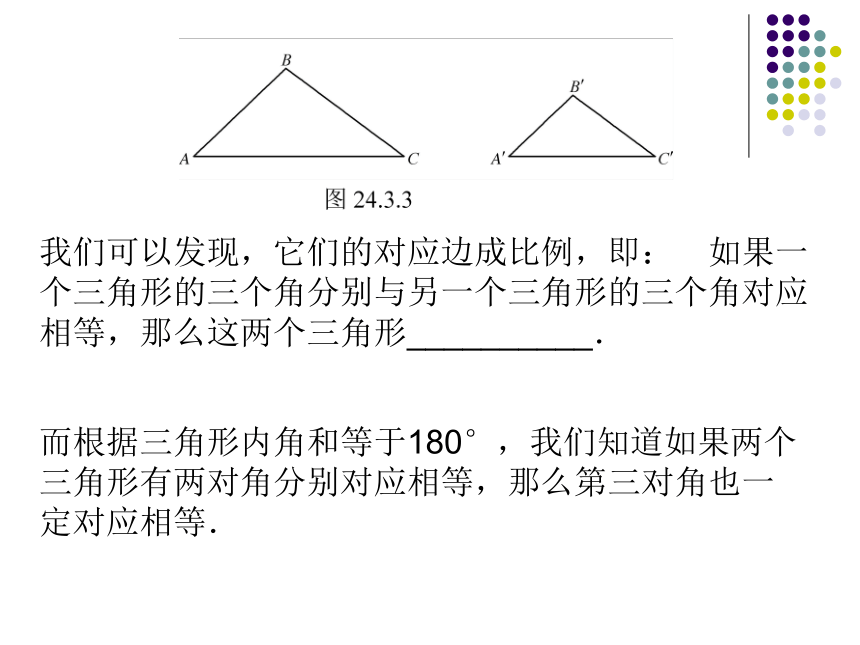
我们可以发现，它们的对应边成比例，即：　如果一个三角形的三个角分别与另一个三角形的三个角对应相等，那么这两个三角形__________．
而根据三角形内角和等于180°，我们知道如果两个三角形有两对角分别对应相等，那么第三对角也一定对应相等．
于是，我们可以得到判定两个三角形相似的一个较为简便的方法：
如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似．
思
考
如果两个三角形仅有一对角是对应相等的，那么它们是否一定相似？
例1 如图24．3．4所示，在两个直角三角形△ABC和△A′B′C′中，∠C＝∠C′＝90°，∠A＝∠A′，证明△ABC∽△A′B′C′．
证明 ∵　∠C＝∠C′＝90°，
∠A＝∠A′，
∴　△ABC∽△A′B′C′（如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似）．
例2 如图24．3．5，△ABC中，DE∥BC，EF∥AB，证明：　△ADE∽△EFC．
证明 ∵　DE∥BC，EF∥AB，
∴　∠ADE＝∠B＝∠EFC，
∴　∠AED＝∠C，
∴　△ADE∽△EFC（如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似）．
如果点D恰好是边AB的中点，那么点E是边AC的中点吗？DE和BC又有什么关系呢？
课堂练习
1．找出图中所有的相似三角形．
2．图中DG∥EH∥FI∥BC，找出图中所有的相似三角形．
习题24．3
1．　判断下面各组中两个三角形是否相似，如果相似，请写出证明过程．
（1）　如图，DE∥BC，△ABC与△ADE；
（2）　如图，∠AED＝∠C，△ABC与△ADE．