3.3相似三角形的判定与性质 应用

(共12张PPT)
相似三角形的判定与性质 应用举例
郴州市第六中学
相似三角形的判定与性质应用举例
★学习目标：
＠ 应用相似三角形的判定与性质进行线段长度的 计算，图形面积的计算或证明几何命题。
＠熟练开放性题型培养解决这类题型的能力。
〖课前基础练习〗
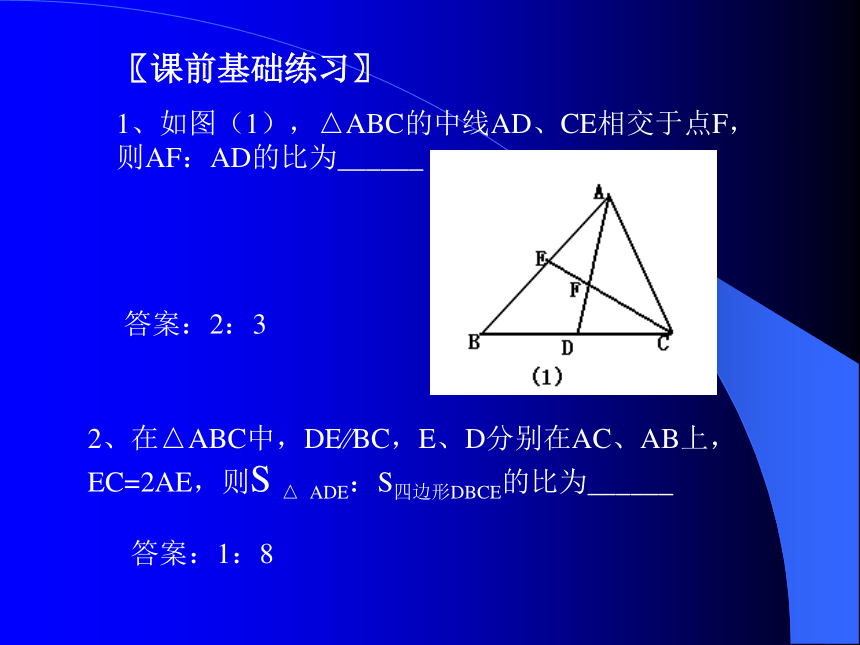
1、如图（1），△ABC的中线AD、CE相交于点F，则AF：AD的比为______
2、在△ABC中，DE BC，E、D分别在AC、AB上，EC=2AE，则S △ ADE：S四边形DBCE的比为______
答案：2：3
答案：1：8
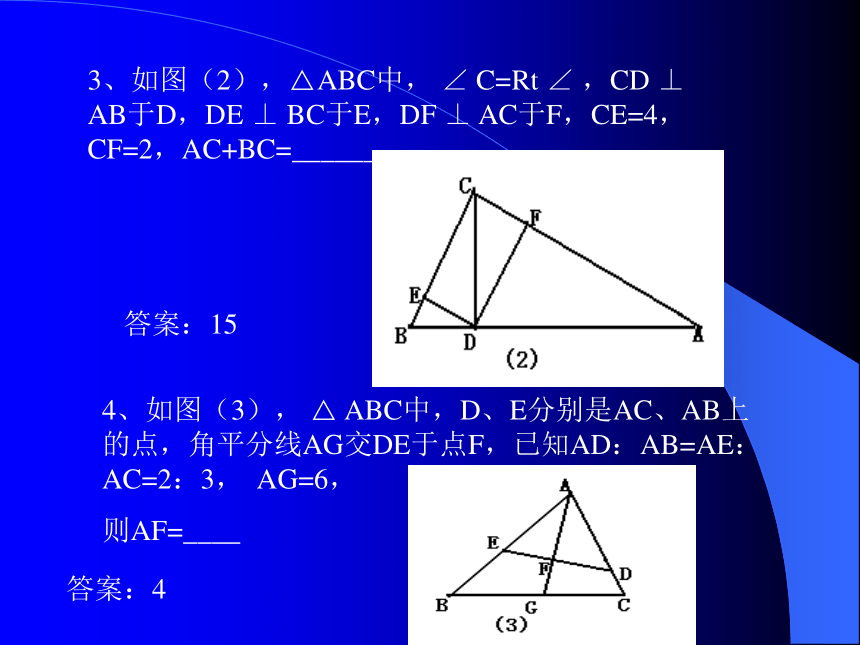
3、如图（2），△ABC中， ∠ C=Rt ∠ ，CD ⊥ AB于D，DE ⊥ BC于E，DF ⊥ AC于F，CE=4，CF=2，AC+BC=_______
4、如图（3）， △ ABC中，D、E分别是AC、AB上的点，角平分线AG交DE于点F，已知AD：AB=AE：AC=2：3， AG=6，
则AF=____
答案：15
答案：4
〖例题讲解 〗
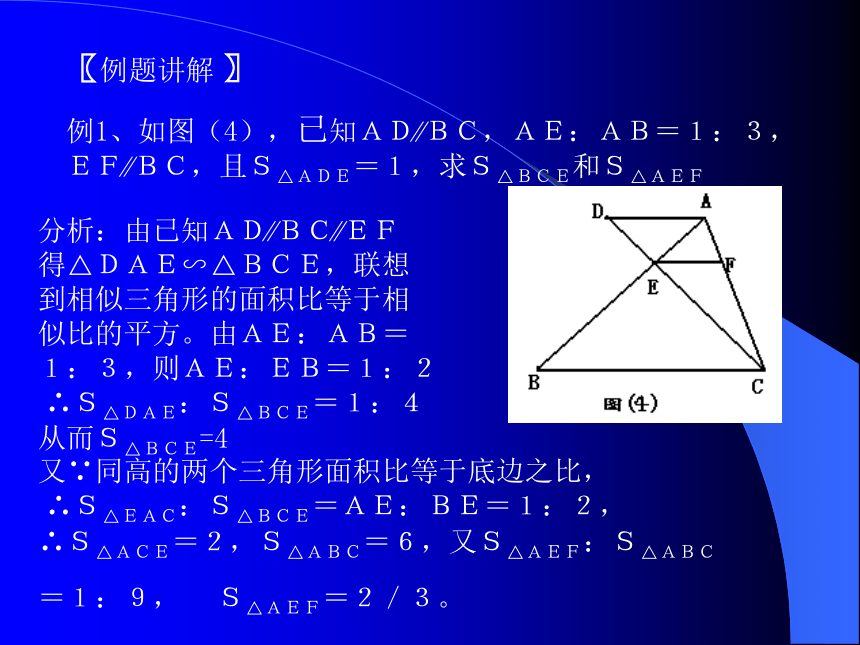
例1、如图（4），已知ＡＤ ＢＣ，ＡＥ：ＡＢ＝１：３，ＥＦ ＢＣ，且Ｓ△ＡＤＥ＝１，求Ｓ△ＢＣＥ和Ｓ△ＡＥＦ
分析：由已知ＡＤ ＢＣ ＥＦ
得△ＤＡＥ∽△ＢＣＥ，联想
到相似三角形的面积比等于相
似比的平方。由ＡＥ：ＡＢ＝
１：３，则ＡＥ：ＥＢ＝１：２
∴Ｓ△ＤＡＥ：Ｓ△ＢＣＥ＝１：４
从而Ｓ△ＢＣＥ=4
又∵同高的两个三角形面积比等于底边之比，
∴Ｓ△ＥＡＣ：Ｓ△ＢＣＥ＝ＡＥ：ＢＥ＝１：２，
∴Ｓ△ＡＣＥ＝２，Ｓ△ＡＢＣ＝６，又Ｓ△ＡＥＦ：Ｓ△ＡＢＣ
＝１：９， Ｓ△ＡＥＦ＝２／３。
例２、已知如图（５），Ｄ是ＡＣ边上的一点，
ＢＥ ＡＣ，ＢＥ＝ＡＤ，ＡＥ分别交ＢＤ、ＢＣ于点Ｆ、Ｇ， ∠ １＝ ∠ ２。
（１）图中哪个三角形与△ＦＡＤ全等？证明你的结论。（２）求证：ＢＦ２＝ＦＧ*ＥＦ。
分析（１）图中△ＢＥＦ与△ＦＡＤ全等。
由ＢＥ ＡＣ， 得∠ １＝ ∠ Ｅ
且∠ＤＦＡ＝ ∠ＢＦＥ，ＢＥ＝ＡＤ
得△ＢＥＦ≌△ＦＡＤ；
（２）由∠ １＝ ∠ ２，而∠ １＝ ∠ Ｅ
∴ ∠ ２＝ ∠ Ｅ，于是△ＢＦＧ∽ △ＢＥＦ
可证ＢＦ２＝ＦＧ*ＥＦ。
〖课内追踪练习〗
１、如图（６）， △ＡＢＣ中，ＤＥ ＦＧ ＢＣ，ＡＤ＝ＤＦ＝ＦＢ，则Ｓ△ＡＤＥ:Ｓ四边形ＤＦＧＥ:Ｓ四边形ＦＢＣＧ=_________
２、如图（７），ＢＣ是⊙Ｏ的直径，ＡＤ⊥ＢＣ于Ｄ，已知ＡＤ＝２，ＢＤ＝１，则⊙Ｏ的半径长是____
答案：１：３：５
答案：２.５
★复习小结
本节主要利用相似三角形的判定和性质进行计算和证明，要求学生能灵活运用所学知识，随着近几年来开放题型的增加，已引起大家的重视，这部分知识还可同方程、函数等综合起来。
〖巩固练习〗
1、两个相似三角形的面积比为5，周长比为m，则5/m=_____
2、如图（8），AC ⊥ AB于A，BD ⊥ AB于B，AD和BC相交于E，EF ⊥ AB于F，已知AC=20，BD=30，则EF的长为____
答案：（1）
答案：（2）12
3、如图（9），在△ ABC中，D是BC的中点，AD=AC，DE ⊥ BC，DE与BA交于点E，EC与AD相交于F，（1）求证： △ ABC ∽ △ FCD；（2）若S △ FCD=5，BC=10，求DE的长。
解：（1）证明： ∵ ED是BC的中垂线
∴ ∠ B=∠ECB ∵AD=AC
∴ ∠ADC=∠ACD ∴ △ ABC ∽ △ FCD
（2）过A作AG ⊥ BC于G
∵ △ ABC ∽ △ FCD
∴ S△ ABC ：S △ FCD=（BC：CD）2=4
∴ S△ ABC=20 又∵BC=10 ∴ AG=4
由已知得BD：BG=2：3 ∵ ED AG
∴ED：AG=BD：BG ∴ED=8/3