3.3相似三角形的判定与性质复习

(共12张PPT)
课题：相似三角形的判定与性质复习课
一、教学目的：
1. 通过复习使学生加深对相似三角形判定与性质的理解。
2.通过复习让学生能熟练掌握一些常见的几何图形中相似三角形判定与性质的应用。
3. 培养学生自行探索、研究、解决问题的能力。
二、教学重点与难点：培养学生应用相似三角形的判定与性质解决相关问题的能力。
三、教学过程：
相似三角形的判定与性质的应用
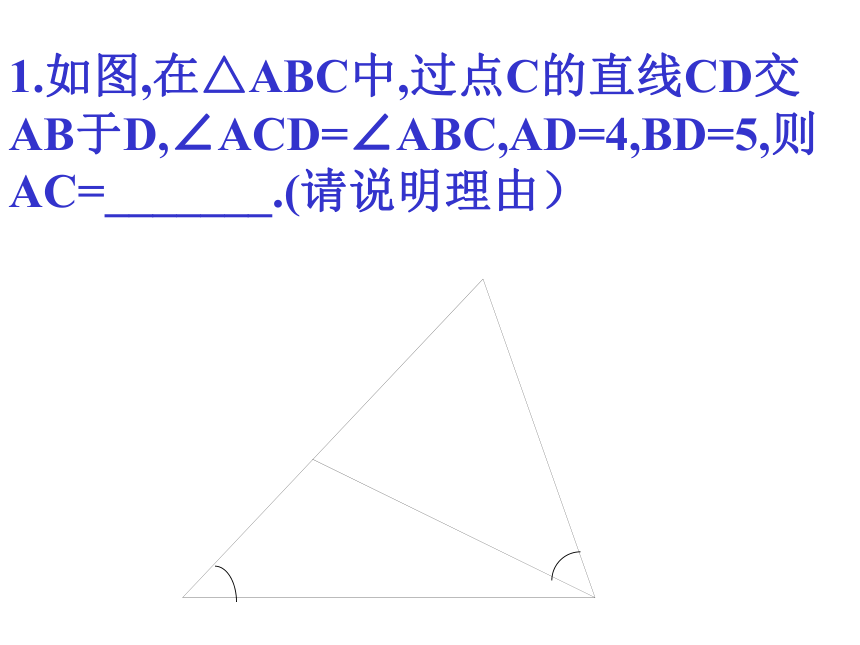
1.如图,在△ABC中,过点C的直线CD交AB于D,∠ACD=∠ABC,AD=4,BD=5,则AC=_______.(请说明理由）
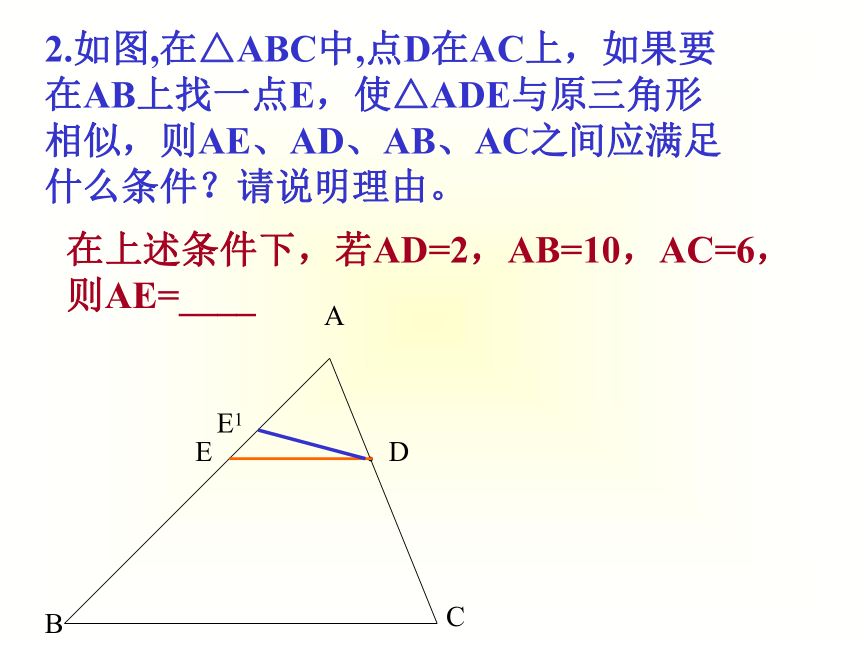
2.如图,在△ABC中,点D在AC上，如果要在AB上找一点E，使△ADE与原三角形相似，则AE、AD、AB、AC之间应满足什么条件？请说明理由。
D
B
C
A
.
E
E1
在上述条件下，若AD=2，AB=10，AC=6，则AE=____
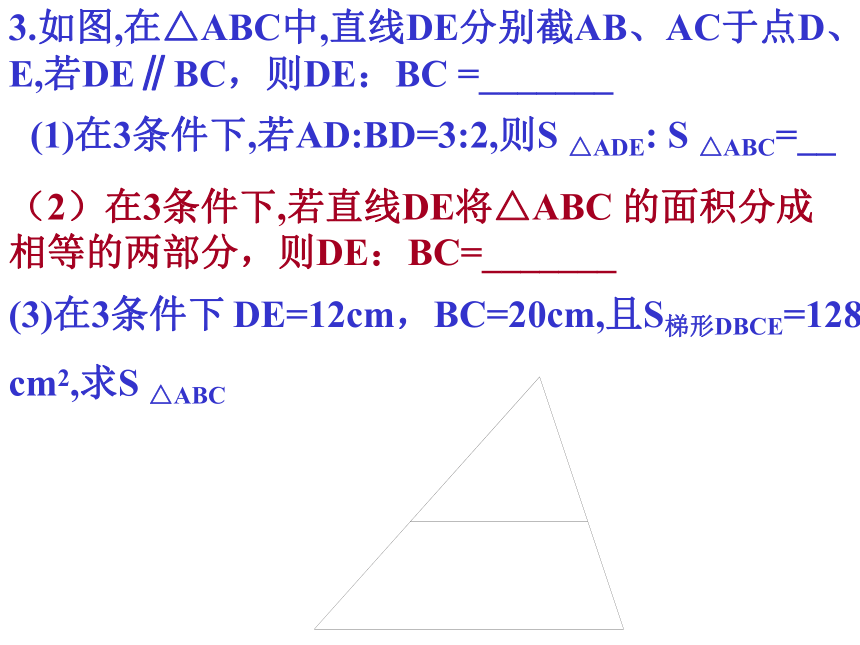
3.如图,在△ABC中,直线DE分别截AB、AC于点D、E,若DE∥BC，则DE：BC =_______
(3)在3条件下 DE=12cm，BC=20cm,且S梯形DBCE=128
cm2,求S △ABC
(1)在3条件下,若AD:BD=3:2,则S △ADE: S △ABC=__
（2）在3条件下,若直线DE将△ABC 的面积分成相等的两部分，则DE：BC=_______
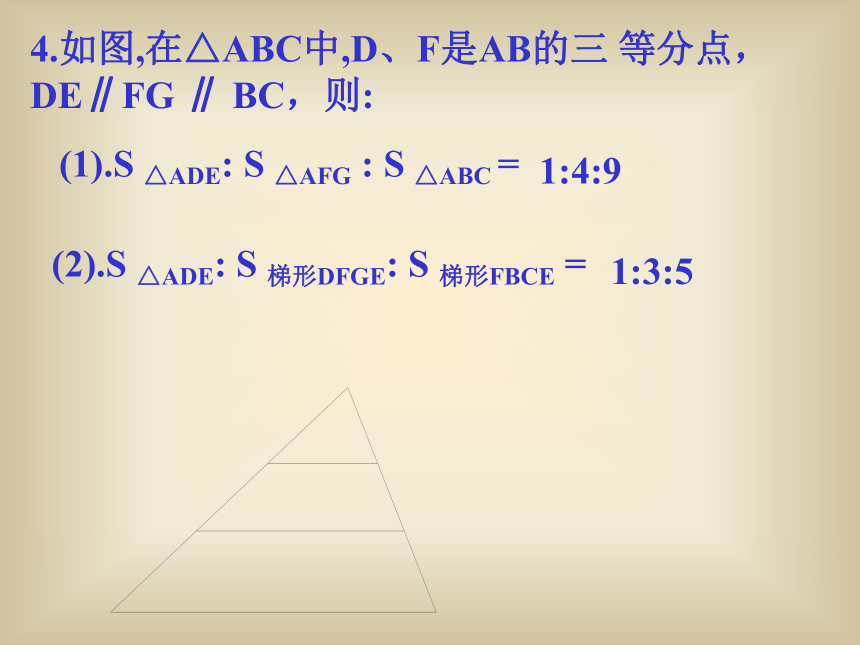
4.如图,在△ABC中,D、F是AB的三 等分点，DE∥FG ∥ BC，则:
1:4:9
(1).S △ADE: S △AFG : S △ABC =
(2).S △ADE: S 梯形DFGE: S 梯形FBCE =
1:3:5
5.如图,在△ABC中, 直线DE分别截AB、AC于 点D、E,若∠AED＝∠ABC, 则DE：BC=____
6.在△ABC中， DE∥BC,连结BE、CD交于点O，则图中有相似三角形几对？请分别写出，并加以说明。
7.在△ABC中， ∠AED＝∠ABC,连结BE、CD交于点O，则图中有相似三角形几对？请分别写出，并加以说明。
8.在△ABC中，若点D、E分别是AB、AC的中点，则各对相似三角形的相似比分别是多少？面积的比呢？
9.在△ABC中， ∠AED＝∠ABC，且点D、E分别是AB、AC的中点，则△ABC是怎样的三角形？
在此条件下图中共有几对相似三角形
如图,在△ABC中,若把条件∠AED＝∠ABC该为BE⊥AC、CD ⊥ AB, 垂足分别为D、E，问：图中共有几对相似三角形？并分别说明理由。
思考题：
作业：
课后记：
本节课的内容为相似三角形的判定与性质的复习课。相似三角形是初中几何中最重要的内容之一，对大部分学生来说也是最难理解的内容之一。为了让学生能自主、合作学习并能很好的掌握，本节课的习题我是把平时最常见的一些图形以变式的方法由浅入深、逐渐推进地把他们串联起来。既有每个学生能独立完成的填空，也有需要小组一起合作、能引起学生思考、有讨论余地的探索题。如第六题有些小组讨论的结果有六对甚至七对相似三角形，实际上我在备课时就想到会有这种情况出现，这主要是学生根据图形的表面现象现象想当然，而没有真正地用定理去推导。还有第三题的（3）的计算，我设计的目的是在求面积的比等于相似比的平方时，应先把两边长进行约分，而在实际求的过程中好多同学把20、12进行平方以后再进行计算，这样计算量就大大增加，此题化的时间比预计的要多，导致后面时间不够。不过从中的收获也更大，学生不仅知道了此题的三种不同的解法，更重要的是明白今后在做这类题目时该怎么办。本节课采用多媒体教学，应该说的效果是不错的，达到了预计的效果。