相似三角形的性质

(共16张PPT)
相似三角形的性质
嘉禾县二中 刘文明
学习目标：
1、 能理解和掌握相似三角形的性质
2、能应用性质解决有关问题
自学指导：
认真看课本P.241的内容，边看书边理解相似三角形的性质。
4分钟后，比谁能做书上的练习。
相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比。
相似三角形的性质定理
一、填空题
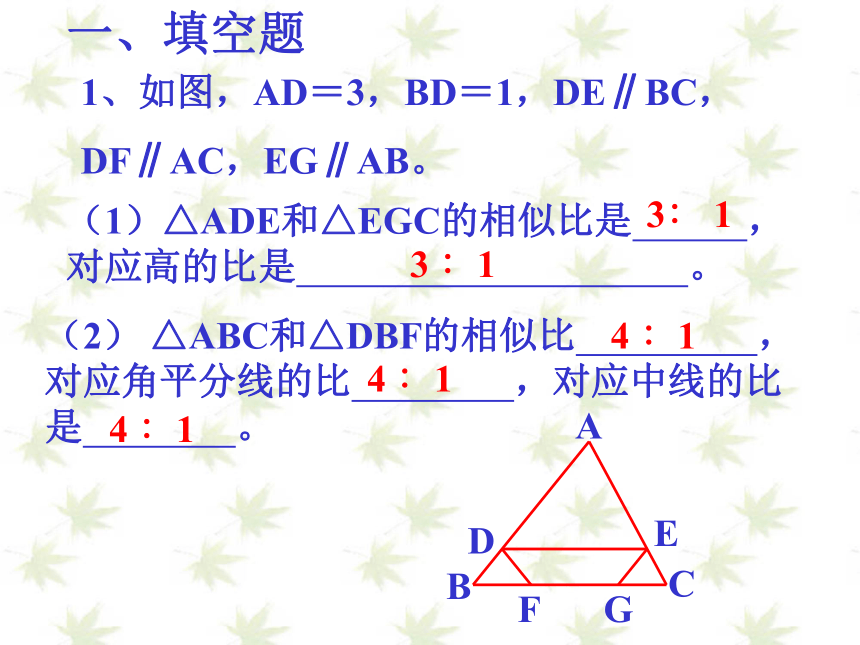
1、如图，AD＝3，BD＝1，DE∥BC，
DF∥AC，EG∥AB。
（1）△ADE和△EGC的相似比是 ，对应高的比是 。
（2） △ABC和△DBF的相似比 ，对应角平分线的比 ，对应中线的比是 。
C
B
A
D
E
F
G
3∶ 1
4 ∶1
4 ∶1
4 ∶1
3 ∶1
2、两个相似三角形的相似比为1 ∶3，它们的对应高的比是 。
3、两个相似三角形的相似比为2∶3，它们的对应中线的比是 。
4、两个相似三角形的对应高的比为3∶5，它们的对角平分线的比是 。
5、两个相似三角形的对应中线的比为9∶16，它们的相似比是 。
6、两个相似三角形的对应角平分线的比为4∶9，它们的对应高的比是 。
7、两个相似三角形各自的最长边分别是7cm、5cm，它们的对应高的比是 。
1∶3
2∶3
3∶5
9∶16
4∶9
7∶5
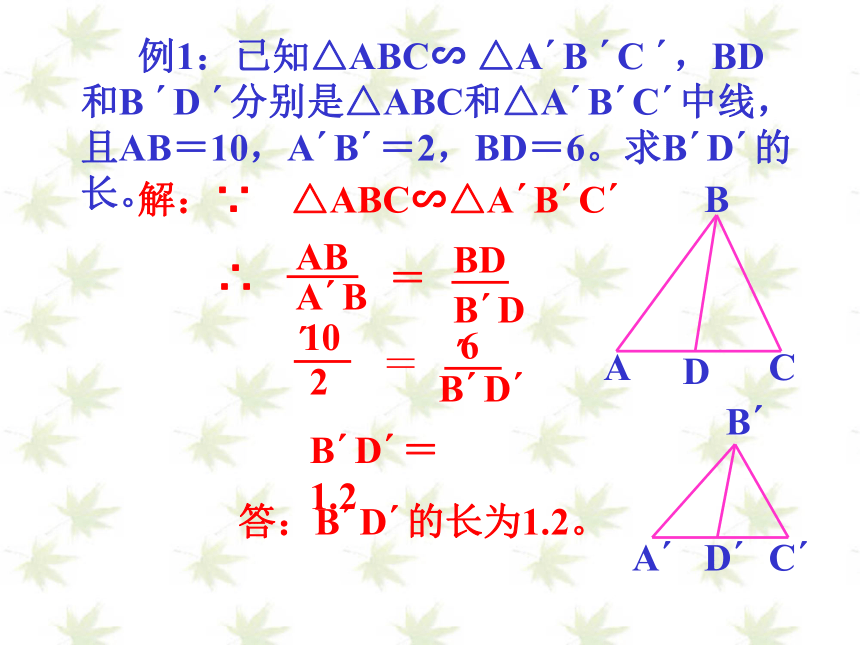
例1：已知△ABC∽ △A B C ，BD和B D 分别是△ABC和△A B C 中线，且AB＝10，A B ＝2，BD＝6。求B D 的长。
解：∵　△ABC∽△A B C
∴　
＝
＝
B D ＝1.2
答：B D 的长为1.2。
AB
A B
BD
B D
10
2
6
B D
A
B
C
D
A
B
C
D
例2：已知△ABC∽△DEF，BG、EH分别是△ABC和 △DEF的角平分线，BC＝6cm,EF＝4cm,BG＝4.8cm.求EH的长。
解：∵ △ABC∽△DEF 　
∴　BC∶EF＝BG∶EH
6∶4＝4.8∶EH
EH＝3.2(cm)
答：EH的长为3.2cm。
A
G
B
C
D
E
F
H
二、判断题
1、相似三角形中，对应线段的比都等于相似比（ ）
2、相似三角形中高的比、中线的比、角平分线的比都等于相似比（ ）
3、两个相似三角形对应角平分线的比1∶3，它们的对应高的比为1∶3（ ）
×
√
√
三、选择题
1、已知△ABC∽△A B C ，AD、A D 分别是对应边BC、B C 上的高，若BC＝8cm,B C ＝6cm,AD＝4cm,则A D 等于（ ）
A 16cm B 12 cm C 3 cm D 6 cm
2、两个相似三角形对应高的比为3∶7，它们的对应角平分线的比为（ ）
A 7∶3 B 49∶9 C 9∶49 D 3∶7
C
D
1、如图△ABC中， DE∥BC，AD＝2.5，DB＝3.5，AF⊥BC于F，交DE于G，AG＝2。求AF的长。
A
B
C
D
E
G
F
图1
2、如图△ABC中，AB＝7，AD＝4，∠B＝∠ACD，求AC的长。
A
B
C
D
图2
3、如图，四边形ABCD中，∠A＝∠BCD＝90°过C作对角线BD的垂线交BD、AD于点E、F。
求证：CD ＝DF·DA
A
B
C
D
E
F
图3
总结：
通过今天的学习你有何收获？从你身边同学的身上你学到了什么？
作业
1、完成教材习题5.4A组P.247T.1.2.3。
2、完成相应练习册的习题。