相似三角形的性质和判定（1）

(共15张PPT)
相似三角形的性质和判定（1）
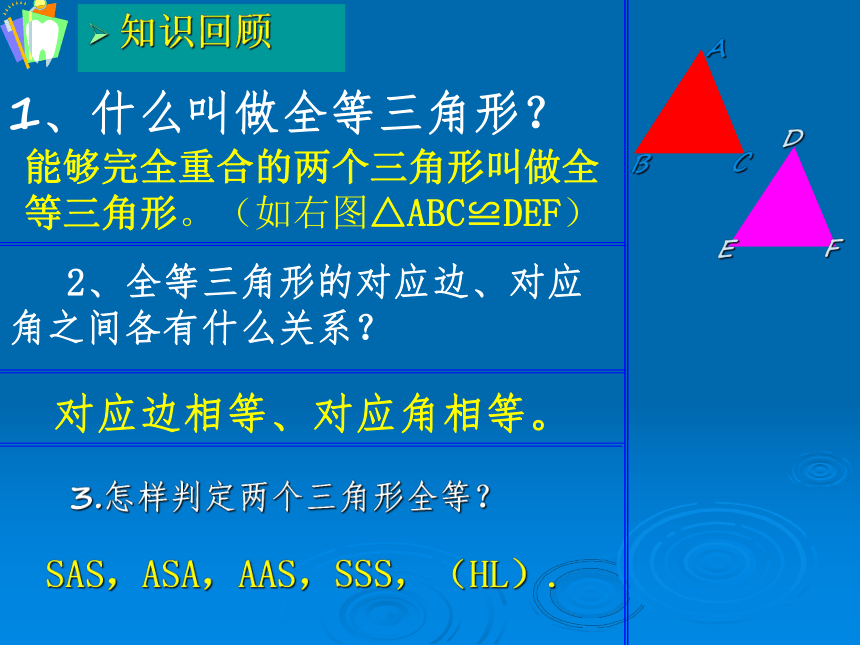
3.怎样判定两个三角形全等？
1、什么叫做全等三角形？
能够完全重合的两个三角形叫做全等三角形。（如右图△ABC≌DEF）
2、全等三角形的对应边、对应角之间各有什么关系？
对应边相等、对应角相等。
A
B
C
D
E
F
SAS，ASA，AAS，SSS，（HL）.
知识回顾
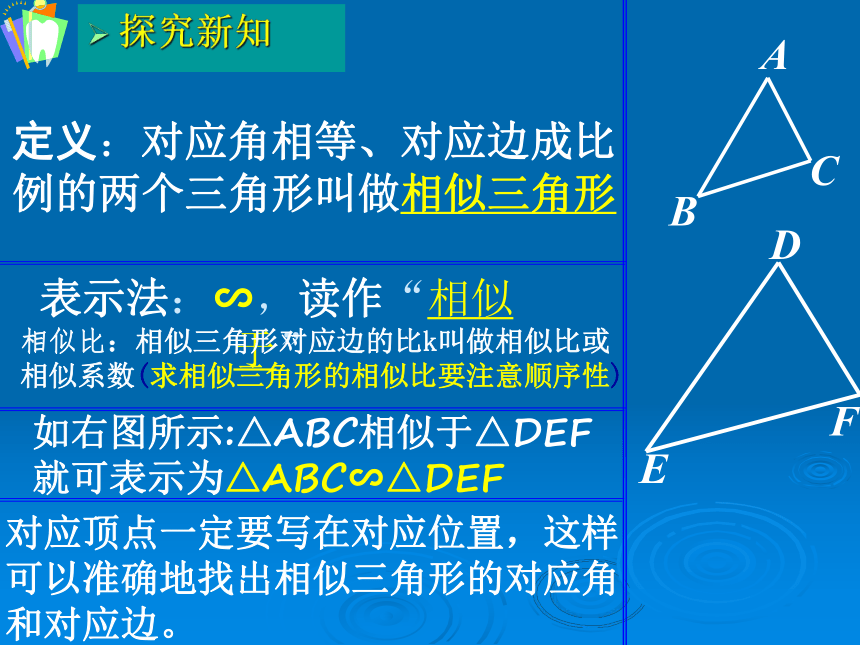
定义：对应角相等、对应边成比例的两个三角形叫做相似三角形
表示法：∽，读作“相似于”
如右图所示:△ABC相似于△DEF就可表示为△ABC∽△DEF
对应顶点一定要写在对应位置，这样可以准确地找出相似三角形的对应角和对应边。
相似比：相似三角形对应边的比k叫做相似比或相似系数(求相似三角形的相似比要注意顺序性)
探究新知
A
B
C
E
D
F
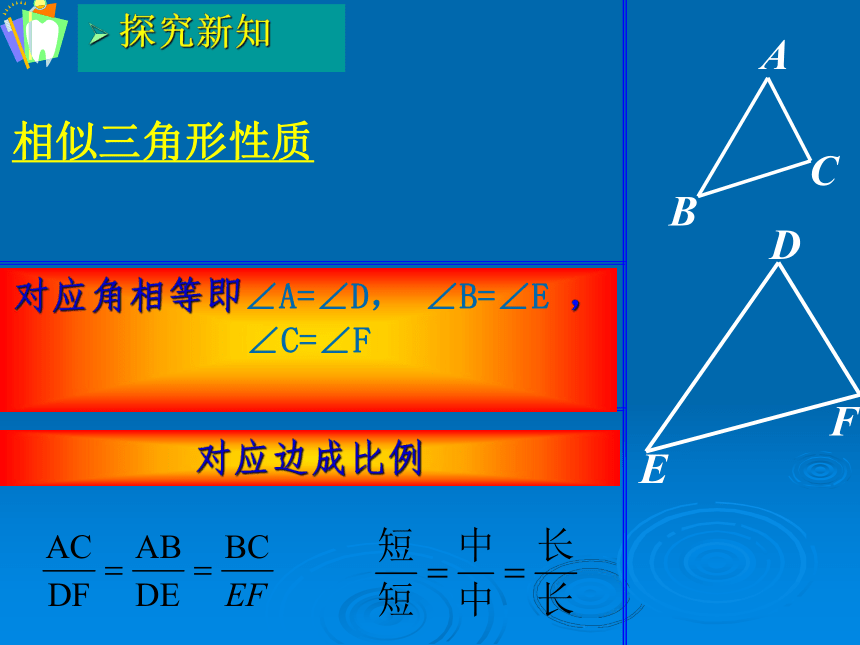
相似三角形性质
A
B
C
E
D
F
探究新知
对应角相等即∠A=∠D， ∠B=∠E ，∠C=∠F
对应边成比例
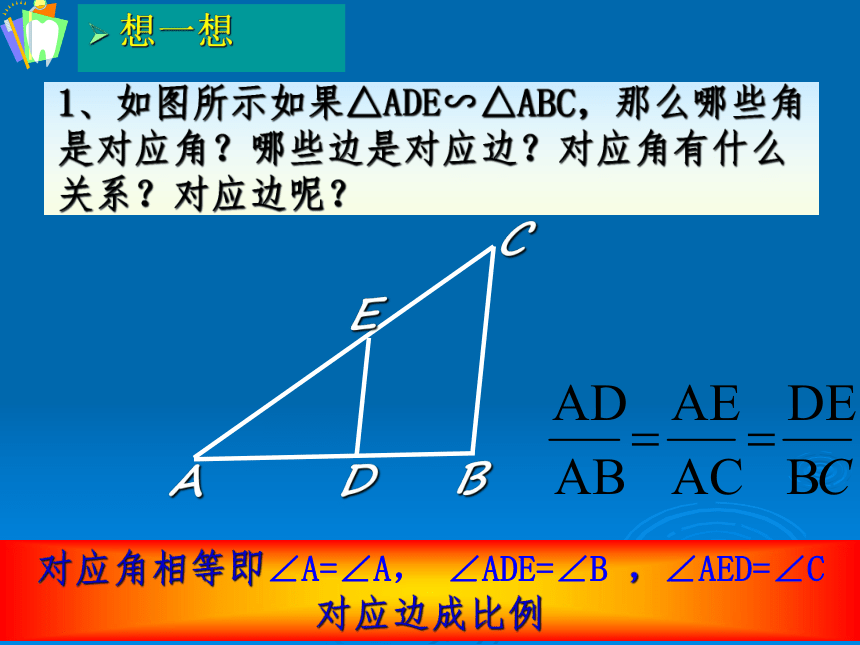
1、如图所示如果△ADE∽△ABC，那么哪些角是对应角？哪些边是对应边？对应角有什么关系？对应边呢？
对应角相等即∠A=∠A， ∠ADE=∠B ，∠AED=∠C
对应边成比例
A
B
C
D
E
想一想
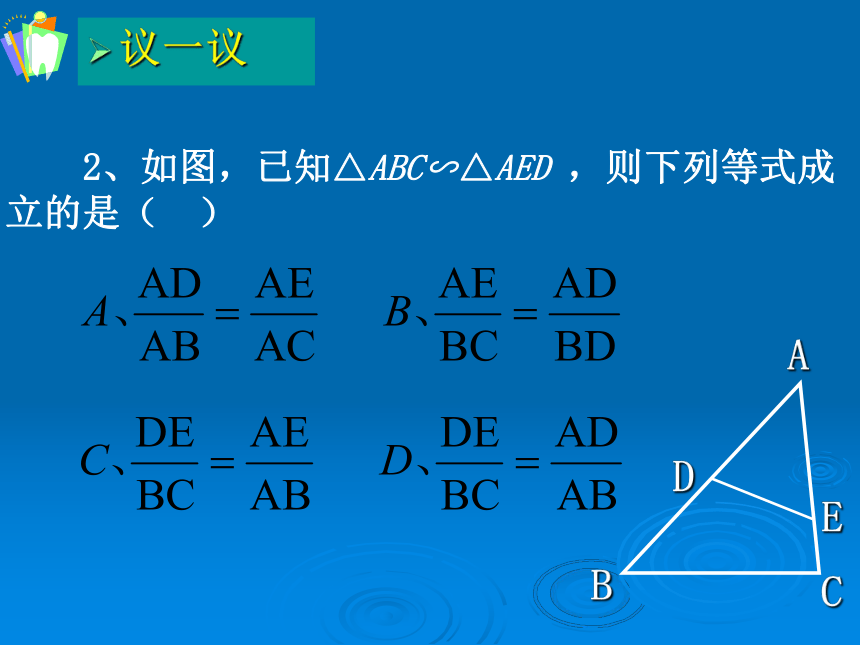
2、如图，已知△ABC∽△AED ，则下列等式成立的是（ ）
E
D
A
B
C
议一议
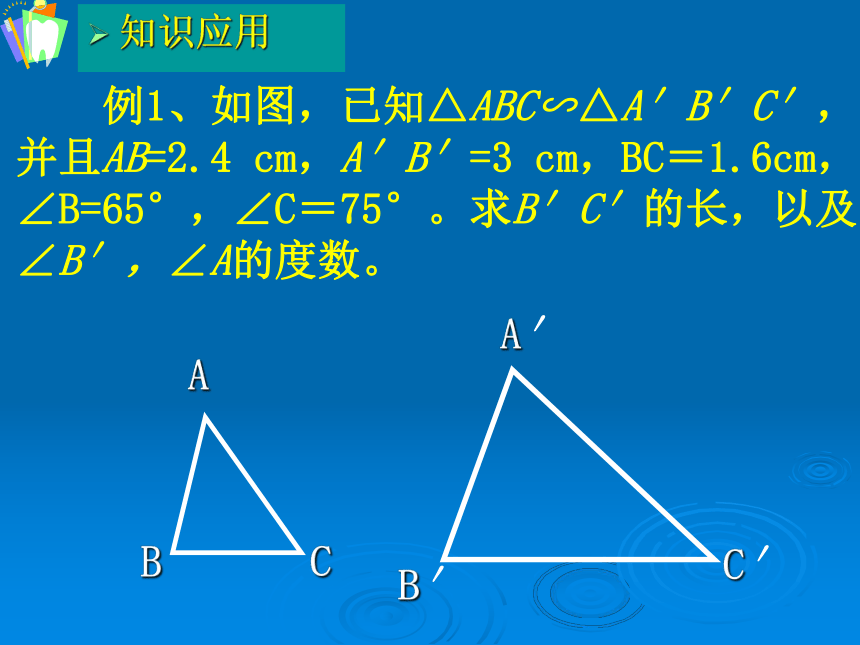
例1、如图，已知△ABC∽△A′B′C′，并且AB=2.4 cm，A′B′=3 cm，BC＝1.6cm，∠B=65°，∠C＝75°。求B′C′的长，以及
∠B′，∠A的度数。
A
B
C
A′
B′
C′
知识应用
如果两个三角形相似，那么它们的三条边对应成比例，反之对吗？
A’
B’
C’
A
B
C
2.1cm
1.8cm
1.5cm
3cm
3.6cm
4.2cm
如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似
探究新知
相似三角形判定1
A’
B’
C’
A
B
C
如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似
探究新知
例2、图中的两个三角形是否相似？
为什么？
A
B
C
2.4cm
1.8cm
2.1cm
E
D
F
3cm
3.5cm
4cm
知识应用
1、若△ABC与△A′B′C′相似，一组对应边的长为AB=3 cm，A′B′=4 cm，那么△A′B′C′与△ABC的相似比是___ _;
2、若△ABC 的三条边长为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm， 那么 △ A′B′C′的最大边长是___ _;
3、若△ABC的三条边长3cm,4cm,5cm,且 △ABC∽△A1B1C1，那么△A1B1C1的形状
是___ _.
4︰3
24cm
直角三角形
知识拓展
这节课你有哪些收获？
课堂小结
课本第73面，1至4题。
课后探究