人教版数学九年级上册 24.2.2切线长定理、三角形的内切圆、内心课件(18张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2.2切线长定理、三角形的内切圆、内心课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 20:56:43 | ||
图片预览


文档简介
切线长与切线长定理
复习
圆的切线的性质:
圆的切线是 过切点的 .
垂直于
半径
P
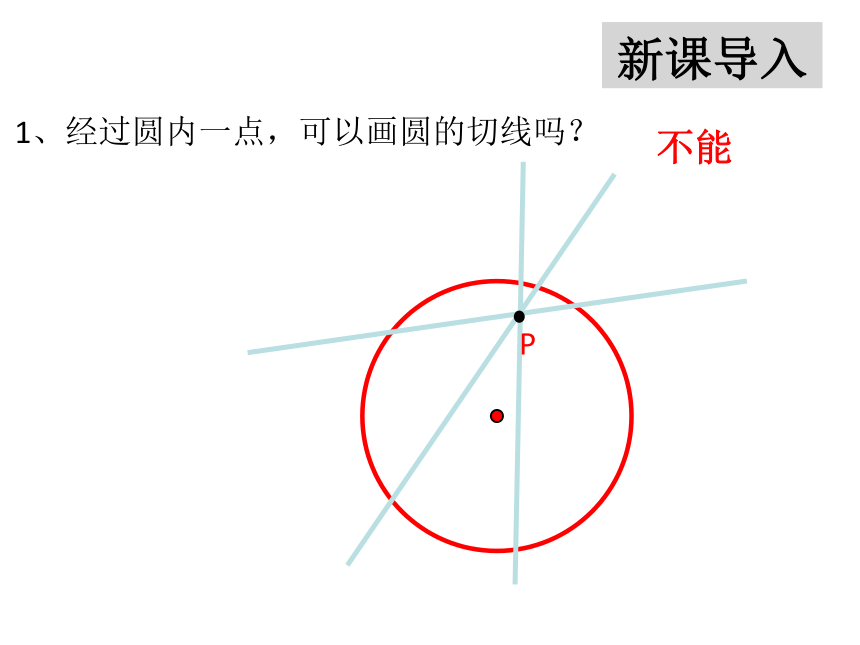
1、经过圆内一点,可以画圆的切线吗?
不能
新课导入
P
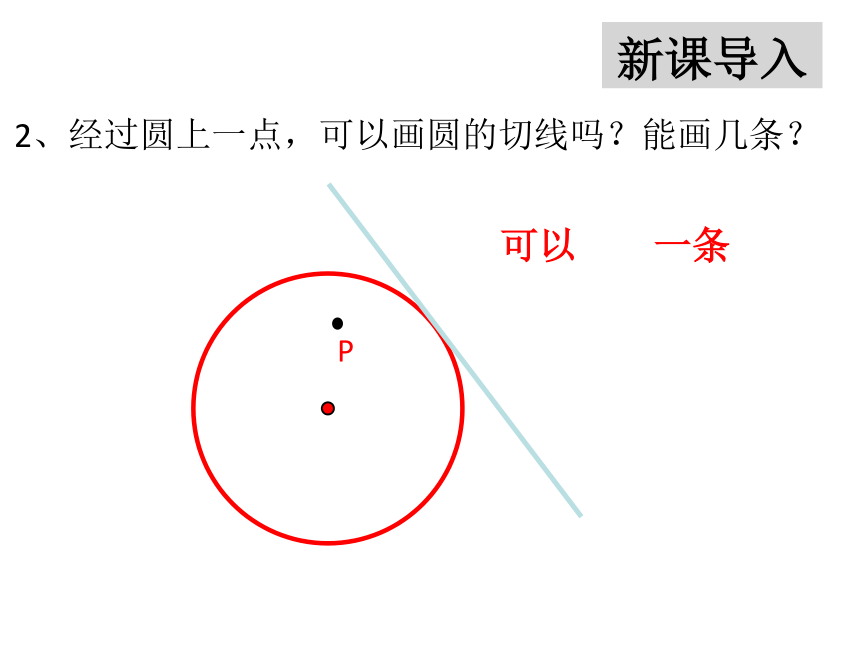
2、经过圆上一点,可以画圆的切线吗?能画几条?
一条
可以
新课导入
P
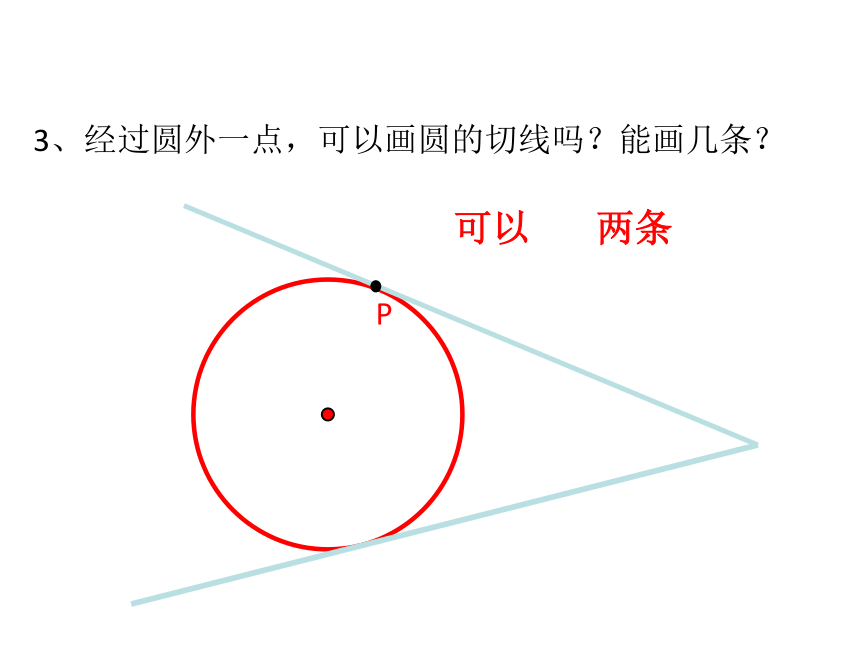
3、经过圆外一点,可以画圆的切线吗?能画几条?
两条
可以
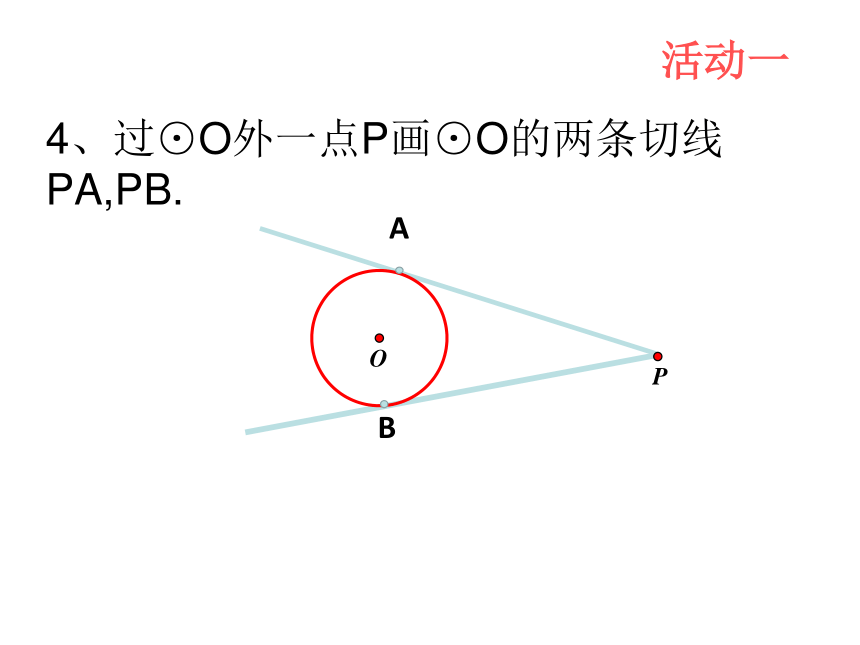
4、过⊙O外一点P画⊙O的两条切线PA,PB.
活动一
A
B
P
O
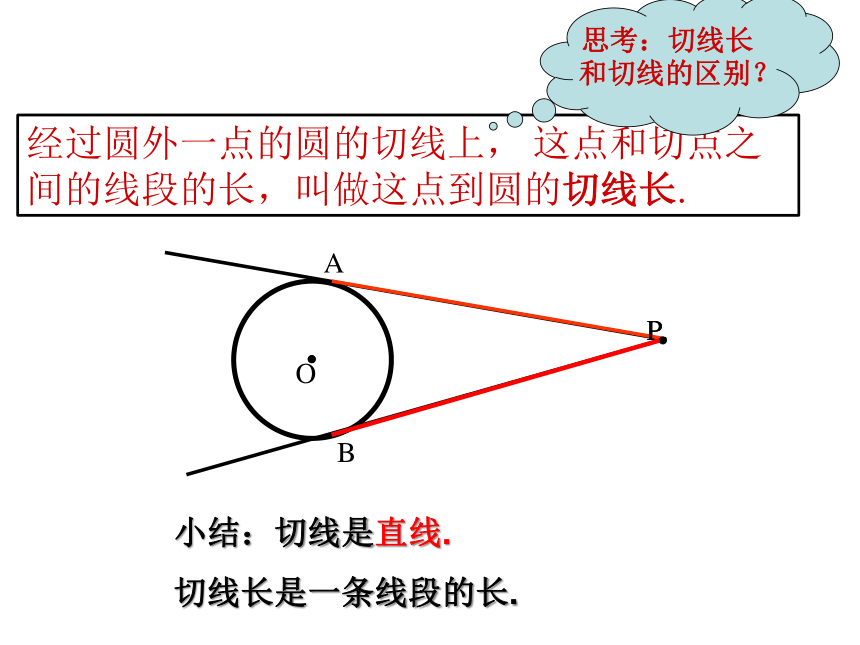
经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这点到圆的切线长.
思考:切线长和切线的区别?
小结:切线是直线.
切线长是一条线段的长.
P
A
B
猜猜切线长PA、PB的数量关系?
猜一猜
PA=PB
如何证明?
如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,连结PO.
求证:PA=PB.
证明:∵PA,PB与⊙O相切,
点A,B是切点,
∴OA⊥PA,OB⊥PB.
即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB
∠1和∠2有什么关系呢?
∠1=∠2
∠1=∠2
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
∵PA、PB分别切⊙O于点A、B,
∴PA=PB
∠1=∠2
切线长定理
几何语言表示
1、判断
(1)过任意一点总可以作圆的两条切线.( )
(2)从圆外一点引圆的两条切线,它们的长相等.( )
2、如图,PM、PN都是⊙O的切线,则
(1)图中相等的线段有 .
(2)图中相等的角有哪些?
OM=ON PM=PN
∠MPO= ∠NPO
∠POM= ∠PON
∠OMP= ∠ONP
×
×
巩固练习
25
3、如图PA、PB分别切⊙O于A、B两点,
∠APB=50°,PB=10cm,连接PO,
则∠APO= 度,PA= .
10cm
4、如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若切线长AP=12,∠P=60°,则弦AB的长为 .
12
5、如图,△ABC的三条边BC,AC,AB分别与⊙O相切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= , AC= ,AB= .
11cm
6cm
9cm
6、如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,求∠P的度数.
解:连接OA,OB
∵∠E=60°
∠AOB=2∠E=120°
∵PA、PB是⊙O的切线
∴∠OAP=∠OBP=90°
∴∠P=360°-90°-90?-120?=60°
课堂小结
经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这点到圆的切线长.
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
1、切线长定义:
2、切线长定理:
7、如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知PA=8cm,求ΔPDE的周长.
解:∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB=8,DA=DC,EC=EB
∴C△PDE=PD+DE+PE=PD+DA+EB+PE
=PA+PB=8+8=16
∴ΔPDE的周长为16cm.
再见
复习
圆的切线的性质:
圆的切线是 过切点的 .
垂直于
半径
P
1、经过圆内一点,可以画圆的切线吗?
不能
新课导入
P
2、经过圆上一点,可以画圆的切线吗?能画几条?
一条
可以
新课导入
P
3、经过圆外一点,可以画圆的切线吗?能画几条?
两条
可以
4、过⊙O外一点P画⊙O的两条切线PA,PB.
活动一
A
B
P
O
经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这点到圆的切线长.
思考:切线长和切线的区别?
小结:切线是直线.
切线长是一条线段的长.
P
A
B
猜猜切线长PA、PB的数量关系?
猜一猜
PA=PB
如何证明?
如图,P为⊙O外一点,PA、PB分别切⊙O于点A、B,连结PO.
求证:PA=PB.
证明:∵PA,PB与⊙O相切,
点A,B是切点,
∴OA⊥PA,OB⊥PB.
即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB
∠1和∠2有什么关系呢?
∠1=∠2
∠1=∠2
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
∵PA、PB分别切⊙O于点A、B,
∴PA=PB
∠1=∠2
切线长定理
几何语言表示
1、判断
(1)过任意一点总可以作圆的两条切线.( )
(2)从圆外一点引圆的两条切线,它们的长相等.( )
2、如图,PM、PN都是⊙O的切线,则
(1)图中相等的线段有 .
(2)图中相等的角有哪些?
OM=ON PM=PN
∠MPO= ∠NPO
∠POM= ∠PON
∠OMP= ∠ONP
×
×
巩固练习
25
3、如图PA、PB分别切⊙O于A、B两点,
∠APB=50°,PB=10cm,连接PO,
则∠APO= 度,PA= .
10cm
4、如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若切线长AP=12,∠P=60°,则弦AB的长为 .
12
5、如图,△ABC的三条边BC,AC,AB分别与⊙O相切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= , AC= ,AB= .
11cm
6cm
9cm
6、如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=60°,求∠P的度数.
解:连接OA,OB
∵∠E=60°
∠AOB=2∠E=120°
∵PA、PB是⊙O的切线
∴∠OAP=∠OBP=90°
∴∠P=360°-90°-90?-120?=60°
课堂小结
经过圆外一点的圆的切线上, 这点和切点之间的线段的长,叫做这点到圆的切线长.
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
1、切线长定义:
2、切线长定理:
7、如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知PA=8cm,求ΔPDE的周长.
解:∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB=8,DA=DC,EC=EB
∴C△PDE=PD+DE+PE=PD+DA+EB+PE
=PA+PB=8+8=16
∴ΔPDE的周长为16cm.
再见
同课章节目录
