人教版 数学九年级上册24.2.2切线长定理、三角形的内切圆、内心课件(28张)
文档属性
| 名称 | 人教版 数学九年级上册24.2.2切线长定理、三角形的内切圆、内心课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 390.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 12:01:40 | ||
图片预览


文档简介
24.2 直线和圆的位置关系(4)
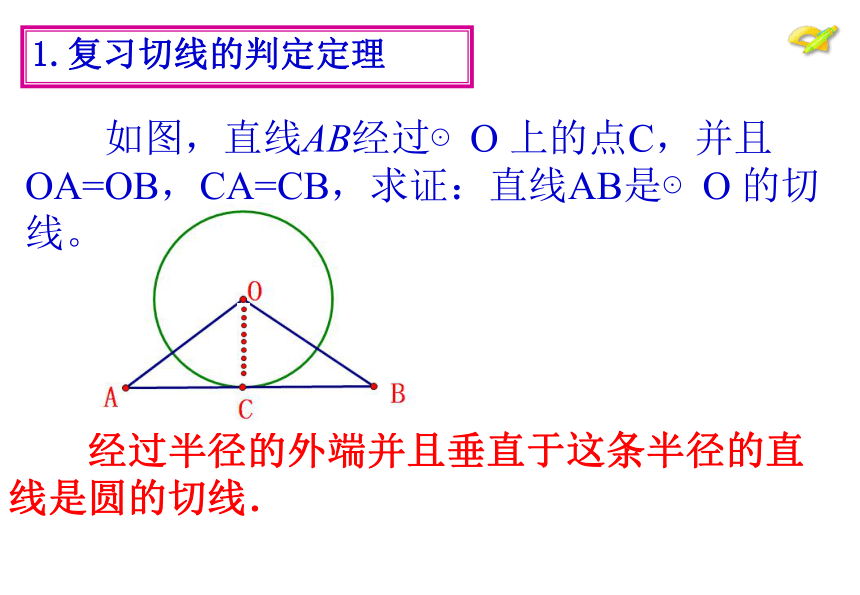
如图,直线AB经过⊙O 上的点C,并且 OA=OB,CA=CB,求证:直线AB是⊙O 的切线。
1.复习切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
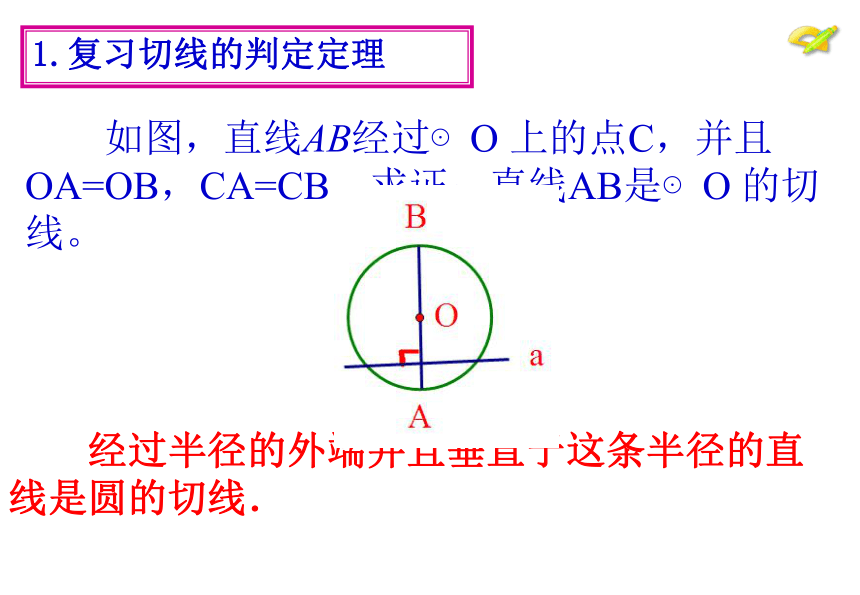
如图,直线AB经过⊙O 上的点C,并且 OA=OB,CA=CB,求证:直线AB是⊙O 的切线。
1.复习切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
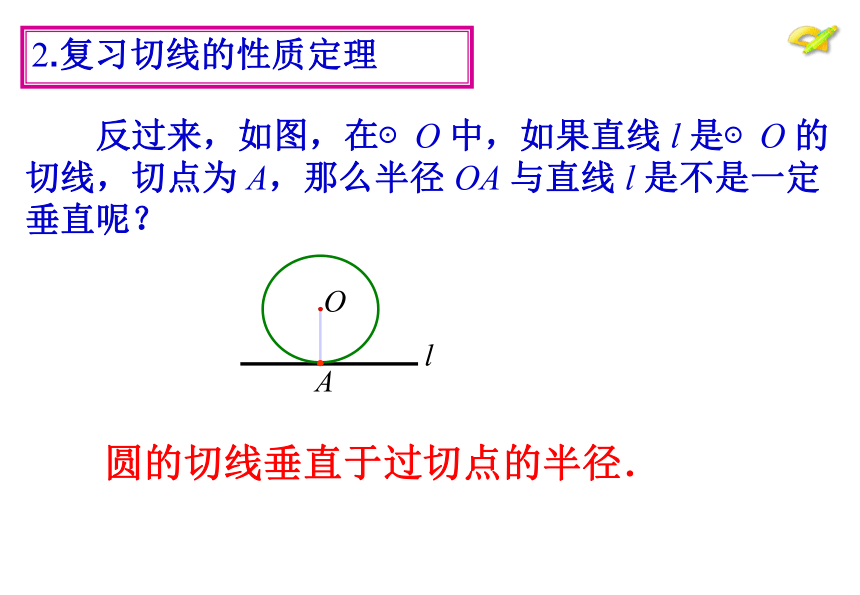
反过来,如图,在⊙O 中,如果直线 l 是⊙O 的切线,切点为 A,那么半径 OA 与直线 l 是不是一定垂直呢?
2.复习切线的性质定理
圆的切线垂直于过切点的半径.
l
O
A
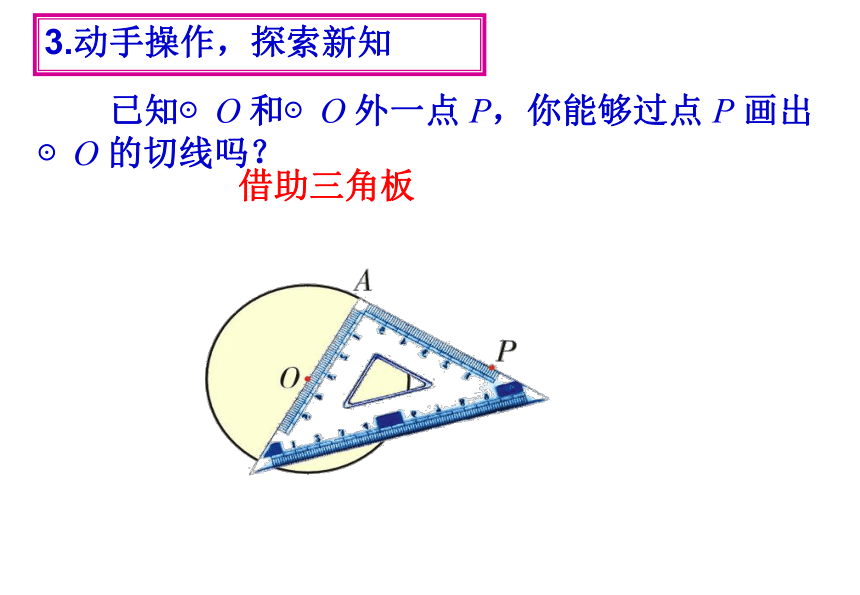
借助三角板
3.动手操作,探索新知
已知⊙O 和⊙O 外一点 P,你能够过点 P 画出⊙O 的切线吗?
·
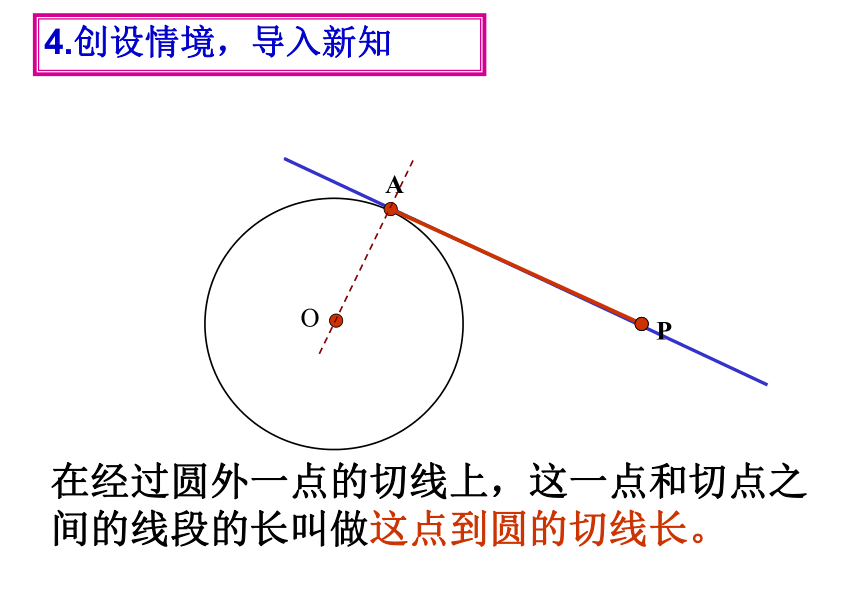
在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长。
O
P
A
4.创设情境,导入新知
探究切线与切线长的区别和联系:
区别
联系
切线
是直线,无法度量。
切线长是切线上一部分
切线长
圆外一点与切点间的距离,可度量。
·
O
P
A
B
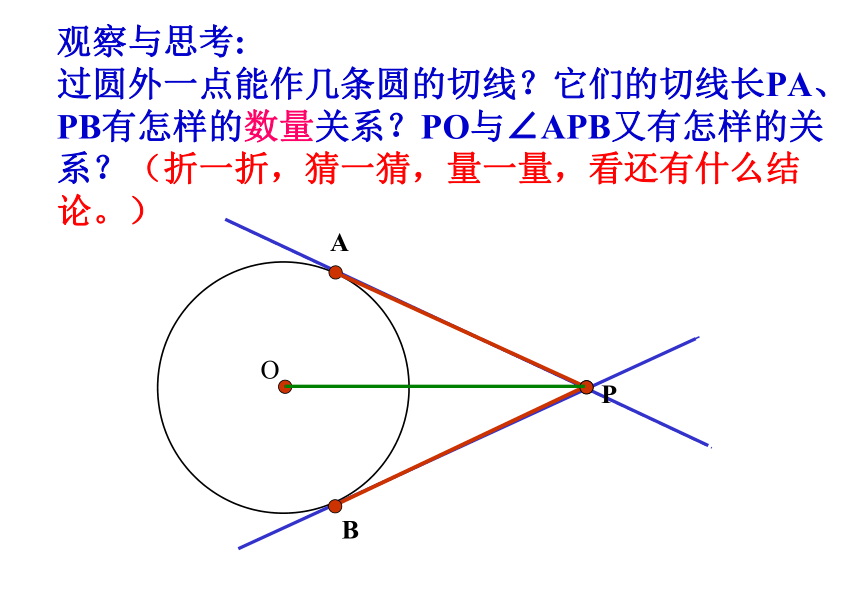
观察与思考:
过圆外一点能作几条圆的切线?它们的切线长PA、PB有怎样的数量关系?PO与∠APB又有怎样的关系?(折一折,猜一猜,量一量,看还有什么结论。)
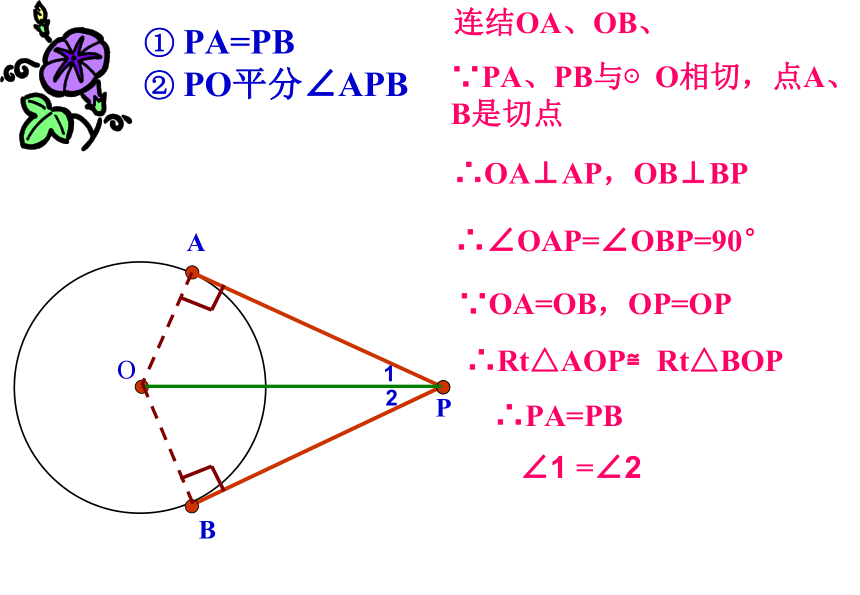
∴Rt△AOP≌Rt△BOP
·
O
P
A
B
① PA=PB
② PO平分∠APB
1
2
连结OA、OB、
∵PA、PB与⊙O相切,点A、B是切点
∠1 =∠2
∴OA⊥AP,OB⊥BP
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
∴PA=PB
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
·
1
2
B
A
P
PA、PB分别切⊙O于A、B
PA = PB
∠1=∠2
A
B
O
·
1
2
符号表示
P
跟踪训练:判断
1. 圆的切线长就圆的切线的长度。( )
2. 过任意一点总可以作圆的两条切线。( )
错
错
如图, AB、AC、BD是⊙O的切线, 切点分别为P、C、D, 如果AB=5, AC=3, 求BD的长.
典例讲解一
巩固应用
1、如图,PA、PB分别与相切于点A、B,
(1)若PB=12,PO=13,则AO=( )。
(2)若PO=10,AO=6,则PB=( )。
(3)若PA=4,AO=3,则PO=( );
PD=( ) 。
O
B
A
P
2
D
5
8
5
2、已知如图4,PA、PB分别与⊙O相切于点A、B,PO与⊙O相交于点D,且PA=4cm,PD=2cm.求半径OA的长.
巩固应用
小结:
2题与1题不同,不能用算术方法直接得出答案,需要设未知数列方程来解决,这是用代数的方法来解决几何题。(渗透方程思想)
如图, AB、BC、CD分别与⊙O相切于E、F、G, 且AB//CD, BO=6cm, CO=8cm, 求BC的长.
数学建模
典例讲解二
已知⊙O的半径为1, 圆心O到直线a的距离为2, 过a上任一点A作⊙O的切线, 切点为B, 则线段AB的最小值为( )
A、1 B、 C、 D、2
典例讲解三
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
看谁最聪明,能写出哪些更多结论?
拓展提高
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
(3)写出图中所有的全等三角形
(4)
写出图中所有的等腰三角形
(2)写出图中与∠OAC相等的角
拓展提高
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)
写出图中所有的等腰三角形
△ABP, △AOB
(2)写出图中与∠OAC相等的角
∠1=∠2=∠3=∠4
2、通过本节课的实践、探索、交流,你有哪些收获
总结反思
。
P
B
A
O
总结与反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
这节课我们所探索的有关切线长的知识是在给出圆的两条切线的情况下得出的,那么要是圆的三条切线两两相交,又会有什么样的结论呢?如果有四条切线呢?这些问题有待于我们课后去研究,请看课外作业。
结束语
布置作业,延伸课外
探索问题1:
已知:如右图,⊙O是△ABC的内切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AD=4,BC=5,CF=6,
则△ABC的周长是__;
(3)若AB=4,BC=5,AC=6,
则AD=__,BE=__,CF=__
探索问题2:
已知:如图6,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.
若四边形ABCD的周长为20,则AB+CD等于 .。
教科书P101 习题 24.2 第 6 题.
布置作业
谢谢大家!
结束语
如图,直线AB经过⊙O 上的点C,并且 OA=OB,CA=CB,求证:直线AB是⊙O 的切线。
1.复习切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
如图,直线AB经过⊙O 上的点C,并且 OA=OB,CA=CB,求证:直线AB是⊙O 的切线。
1.复习切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
反过来,如图,在⊙O 中,如果直线 l 是⊙O 的切线,切点为 A,那么半径 OA 与直线 l 是不是一定垂直呢?
2.复习切线的性质定理
圆的切线垂直于过切点的半径.
l
O
A
借助三角板
3.动手操作,探索新知
已知⊙O 和⊙O 外一点 P,你能够过点 P 画出⊙O 的切线吗?
·
在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长。
O
P
A
4.创设情境,导入新知
探究切线与切线长的区别和联系:
区别
联系
切线
是直线,无法度量。
切线长是切线上一部分
切线长
圆外一点与切点间的距离,可度量。
·
O
P
A
B
观察与思考:
过圆外一点能作几条圆的切线?它们的切线长PA、PB有怎样的数量关系?PO与∠APB又有怎样的关系?(折一折,猜一猜,量一量,看还有什么结论。)
∴Rt△AOP≌Rt△BOP
·
O
P
A
B
① PA=PB
② PO平分∠APB
1
2
连结OA、OB、
∵PA、PB与⊙O相切,点A、B是切点
∠1 =∠2
∴OA⊥AP,OB⊥BP
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
∴PA=PB
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
·
1
2
B
A
P
PA、PB分别切⊙O于A、B
PA = PB
∠1=∠2
A
B
O
·
1
2
符号表示
P
跟踪训练:判断
1. 圆的切线长就圆的切线的长度。( )
2. 过任意一点总可以作圆的两条切线。( )
错
错
如图, AB、AC、BD是⊙O的切线, 切点分别为P、C、D, 如果AB=5, AC=3, 求BD的长.
典例讲解一
巩固应用
1、如图,PA、PB分别与相切于点A、B,
(1)若PB=12,PO=13,则AO=( )。
(2)若PO=10,AO=6,则PB=( )。
(3)若PA=4,AO=3,则PO=( );
PD=( ) 。
O
B
A
P
2
D
5
8
5
2、已知如图4,PA、PB分别与⊙O相切于点A、B,PO与⊙O相交于点D,且PA=4cm,PD=2cm.求半径OA的长.
巩固应用
小结:
2题与1题不同,不能用算术方法直接得出答案,需要设未知数列方程来解决,这是用代数的方法来解决几何题。(渗透方程思想)
如图, AB、BC、CD分别与⊙O相切于E、F、G, 且AB//CD, BO=6cm, CO=8cm, 求BC的长.
数学建模
典例讲解二
已知⊙O的半径为1, 圆心O到直线a的距离为2, 过a上任一点A作⊙O的切线, 切点为B, 则线段AB的最小值为( )
A、1 B、 C、 D、2
典例讲解三
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
看谁最聪明,能写出哪些更多结论?
拓展提高
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
(3)写出图中所有的全等三角形
(4)
写出图中所有的等腰三角形
(2)写出图中与∠OAC相等的角
拓展提高
切线长定理的基本图形的研究
PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(3)写出图中所有的全等三角形
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
(4)
写出图中所有的等腰三角形
△ABP, △AOB
(2)写出图中与∠OAC相等的角
∠1=∠2=∠3=∠4
2、通过本节课的实践、探索、交流,你有哪些收获
总结反思
。
P
B
A
O
总结与反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。
这节课我们所探索的有关切线长的知识是在给出圆的两条切线的情况下得出的,那么要是圆的三条切线两两相交,又会有什么样的结论呢?如果有四条切线呢?这些问题有待于我们课后去研究,请看课外作业。
结束语
布置作业,延伸课外
探索问题1:
已知:如右图,⊙O是△ABC的内切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AD=4,BC=5,CF=6,
则△ABC的周长是__;
(3)若AB=4,BC=5,AC=6,
则AD=__,BE=__,CF=__
探索问题2:
已知:如图6,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.
若四边形ABCD的周长为20,则AB+CD等于 .。
教科书P101 习题 24.2 第 6 题.
布置作业
谢谢大家!
结束语
同课章节目录
