人教版数学九年级上册 24.2.2 切线长定理课件(15张)
文档属性
| 名称 | 人教版数学九年级上册 24.2.2 切线长定理课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 796.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 11:56:44 | ||
图片预览



文档简介
切线长定理
复习:
切线的判定:
切线的性质:
过平面内的一点作圆的切线,可以作出几条切线?
问题:
探究:
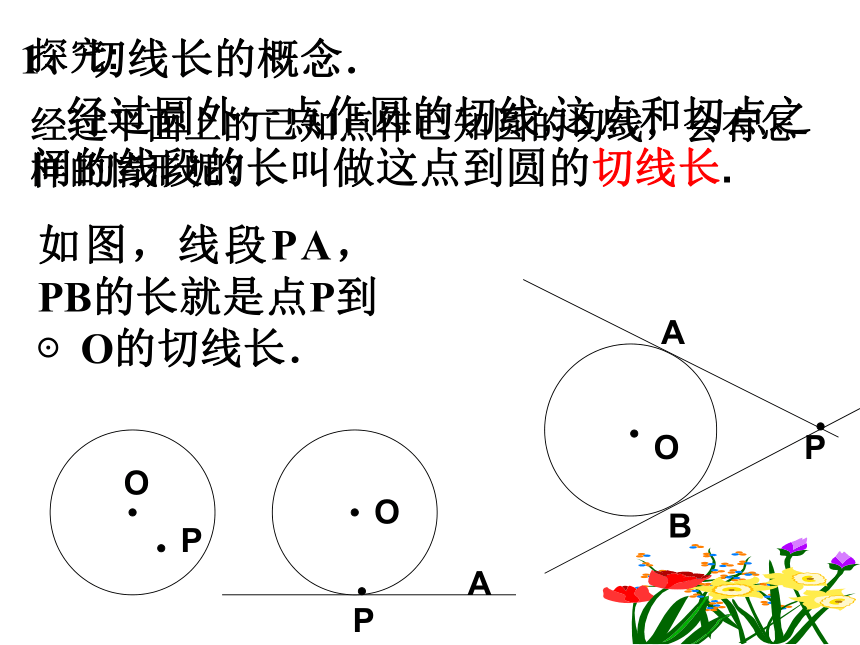
经过平面上的已知点作已知圆的切线,会有怎样的情形呢?
A
P
O
如图,线段PA,PB的长就是点P到⊙O的切线长.
1、切线长的概念.
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
O
A
P
O
B
P
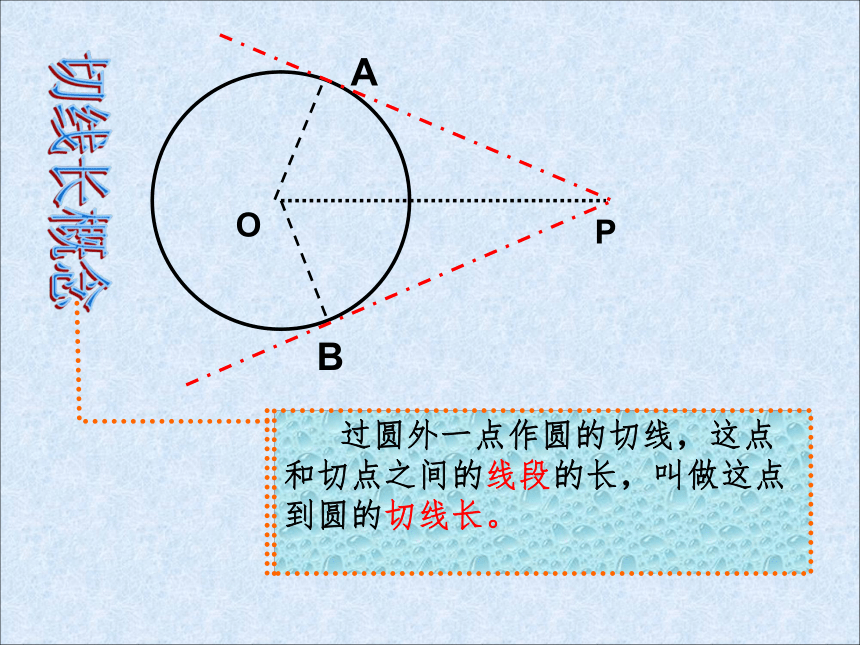
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
O
P
A
B
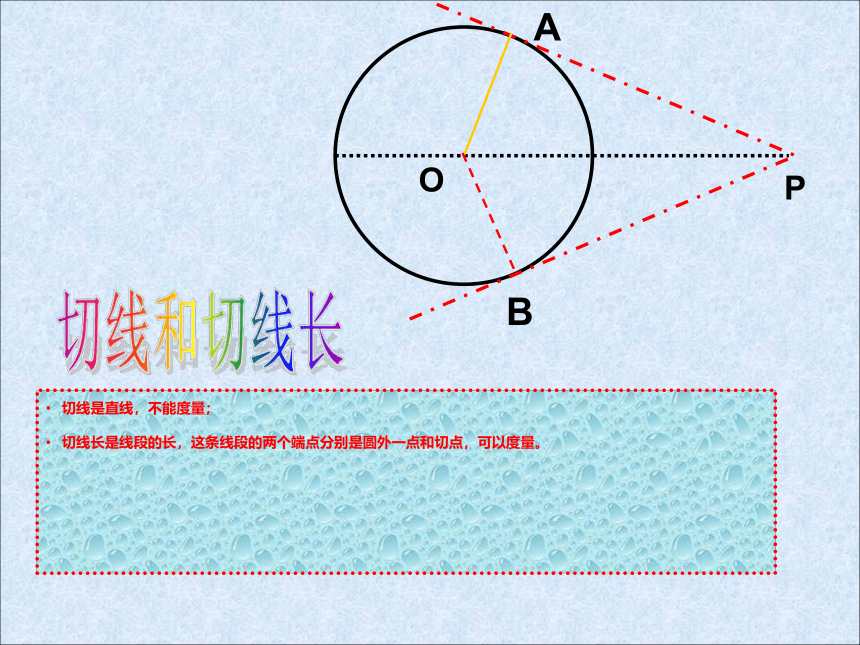
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
切线和切线长
O
P
A
B
O
P
A
B
∟
∟
M
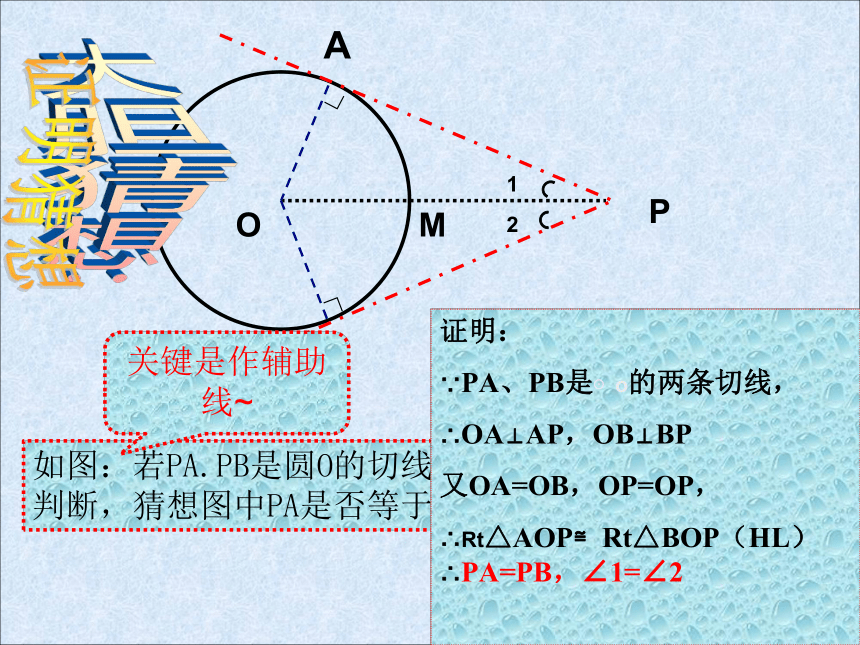
如图:若PA.PB是圆O的切线.A和B是切点.根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
大胆猜想:
⌒
⌒
1
2
证明:
∵PA、PB是⊙o的两条切线,
∴OA⊥AP,OB⊥BP
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,∠1=∠2
证明猜想
关键是作辅助线~
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
P
A
B
例1:如图:PA、PB是⊙O的两条切线,A、B为切点。
。
A
O
C
P
B
思考:由切线长定理可以得出哪些结论?
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形;
(3)写出图中所有的等腰三角形.
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
想一想
练习
1、如图,已知⊙O的半径为3cm,
PO=6cm,PA,PB分别切⊙O于A,B,
(1)PA=______
(2)若PO交⊙O于点Q,直线CD切⊙O
于点Q,交PA、PB于点C、D,则
△PCD的周长是______
O
P
B
A
C
D
Q
2、已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径.求证:AC∥OP.
C
B
A
P
O
课堂小结
通过这节课的复习,你有什么收获或体会?
关于切线长定理,你还有什么不明白的问题?
小结:
(1)切线长定理。
(2)连接圆心和切点是我们解决切线长定理相关问题时常用的辅助线。
作业:
1.?已知圆O是?ABC的内切圆,切点D,E,F,如果AE=1,CD=2,BF=3,且
?ABC的面积为6,求内切圆的半径
2.在
?ABC中角
ABC等于50度,角ACB等于75度,点O是内心,则角BOC等于多少
复习:
切线的判定:
切线的性质:
过平面内的一点作圆的切线,可以作出几条切线?
问题:
探究:
经过平面上的已知点作已知圆的切线,会有怎样的情形呢?
A
P
O
如图,线段PA,PB的长就是点P到⊙O的切线长.
1、切线长的概念.
经过圆外一点作圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长.
O
A
P
O
B
P
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
O
P
A
B
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
切线和切线长
O
P
A
B
O
P
A
B
∟
∟
M
如图:若PA.PB是圆O的切线.A和B是切点.根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
大胆猜想:
⌒
⌒
1
2
证明:
∵PA、PB是⊙o的两条切线,
∴OA⊥AP,OB⊥BP
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,∠1=∠2
证明猜想
关键是作辅助线~
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
O
P
A
B
例1:如图:PA、PB是⊙O的两条切线,A、B为切点。
。
A
O
C
P
B
思考:由切线长定理可以得出哪些结论?
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形;
(3)写出图中所有的等腰三角形.
。
P
B
A
O
(3)连结圆心和圆外一点
(2)连结两切点
(1)分别连结圆心和切点
反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
想一想
练习
1、如图,已知⊙O的半径为3cm,
PO=6cm,PA,PB分别切⊙O于A,B,
(1)PA=______
(2)若PO交⊙O于点Q,直线CD切⊙O
于点Q,交PA、PB于点C、D,则
△PCD的周长是______
O
P
B
A
C
D
Q
2、已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径.求证:AC∥OP.
C
B
A
P
O
课堂小结
通过这节课的复习,你有什么收获或体会?
关于切线长定理,你还有什么不明白的问题?
小结:
(1)切线长定理。
(2)连接圆心和切点是我们解决切线长定理相关问题时常用的辅助线。
作业:
1.?已知圆O是?ABC的内切圆,切点D,E,F,如果AE=1,CD=2,BF=3,且
?ABC的面积为6,求内切圆的半径
2.在
?ABC中角
ABC等于50度,角ACB等于75度,点O是内心,则角BOC等于多少
同课章节目录
