人教版数学九年级上册24.2.2切线长定理课件(15张)
文档属性
| 名称 | 人教版数学九年级上册24.2.2切线长定理课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 12:03:43 | ||
图片预览


文档简介
切线长定理
第24章 圆(12)
1.直线与圆有哪几种位置关系?
直线与圆位置关系: ①相离; ②相切; ③相交.
一、知识回顾:
2.切线的性质定理是什么?
圆的切线垂直于过切点的半径
问题一:
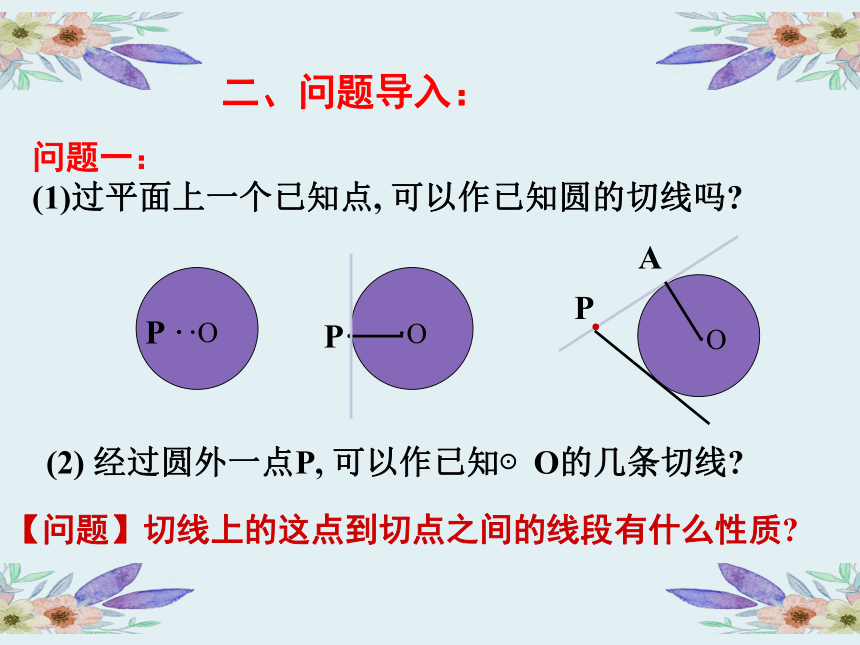
(1)过平面上一个已知点, 可以作已知圆的切线吗?
·O
·O
·O
P ·
P·
A
(2) 经过圆外一点P, 可以作已知⊙O的几条切线?
【问题】切线上的这点到切点之间的线段有什么性质?
二、问题导入:
P
·
·
O
P
B
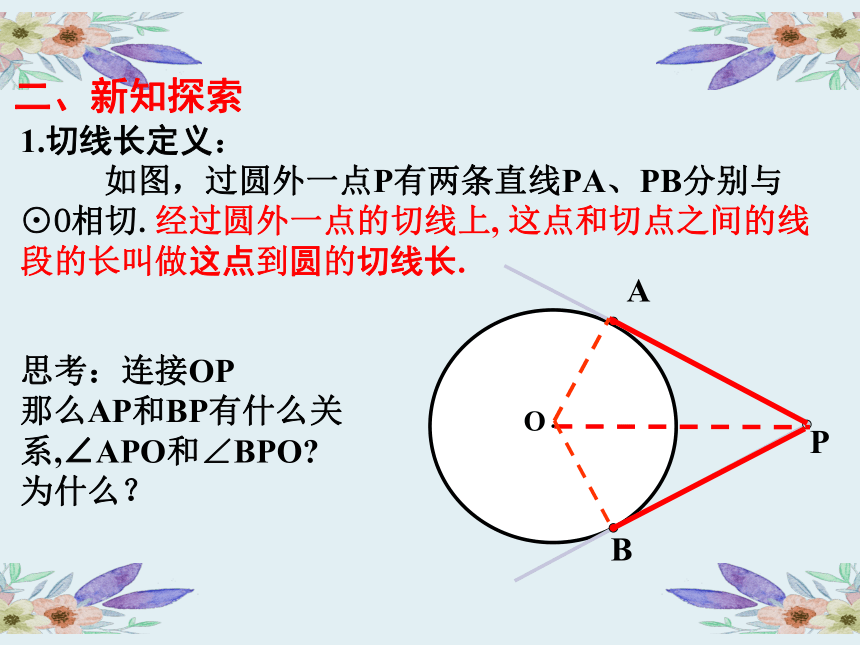
1.切线长定义:
如图,过圆外一点P有两条直线PA、PB分别与⊙O相切.经过圆外一点的切线上, 这点和切点之间的线段的长叫做这点到圆的切线长.
A
二、新知探索
思考:连接OP
那么AP和BP有什么关系,∠APO和∠BPO?
为什么?
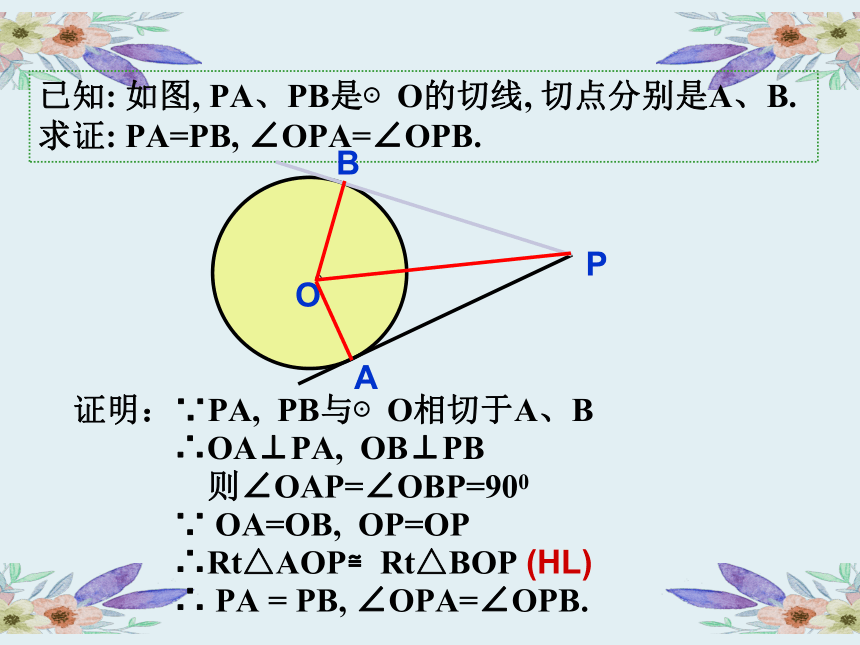
已知: 如图, PA、PB是⊙O的切线, 切点分别是A、B.
求证: PA=PB, ∠OPA=∠OPB.
证明:∵PA, PB与⊙O相切于A、B
∴OA⊥PA, OB⊥PB
则∠OAP=∠OBP=900
∵ OA=OB, OP=OP
∴Rt△AOP≌Rt△BOP (HL)
∴ PA = PB, ∠OPA=∠OPB.
A
P
O
。
B
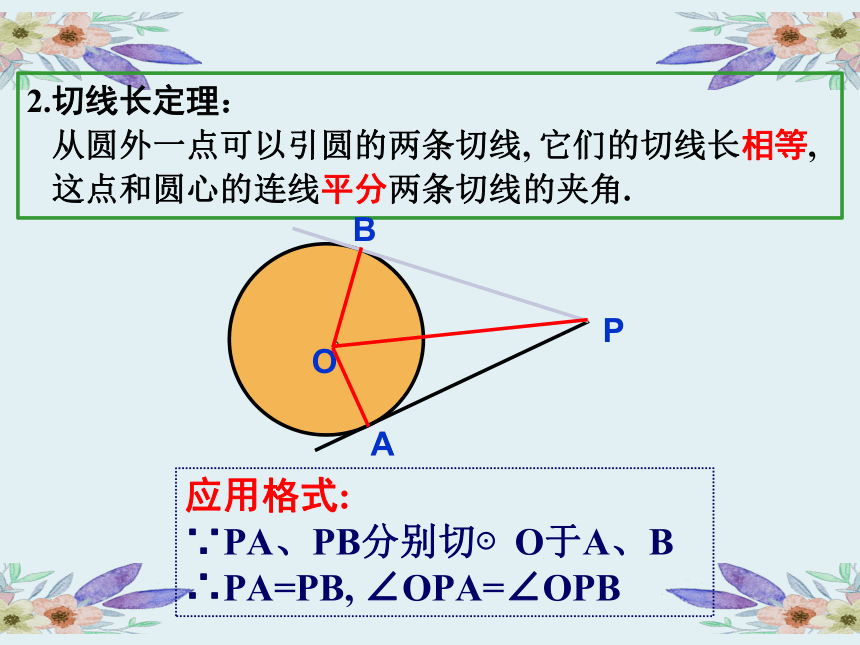
应用格式:
∵PA、PB分别切⊙O于A、B
∴PA=PB, ∠OPA=∠OPB
2.切线长定理:
从圆外一点可以引圆的两条切线, 它们的切线长相等,
这点和圆心的连线平分两条切线的夹角.
A
P
O
。
B
。
A
B
P
O
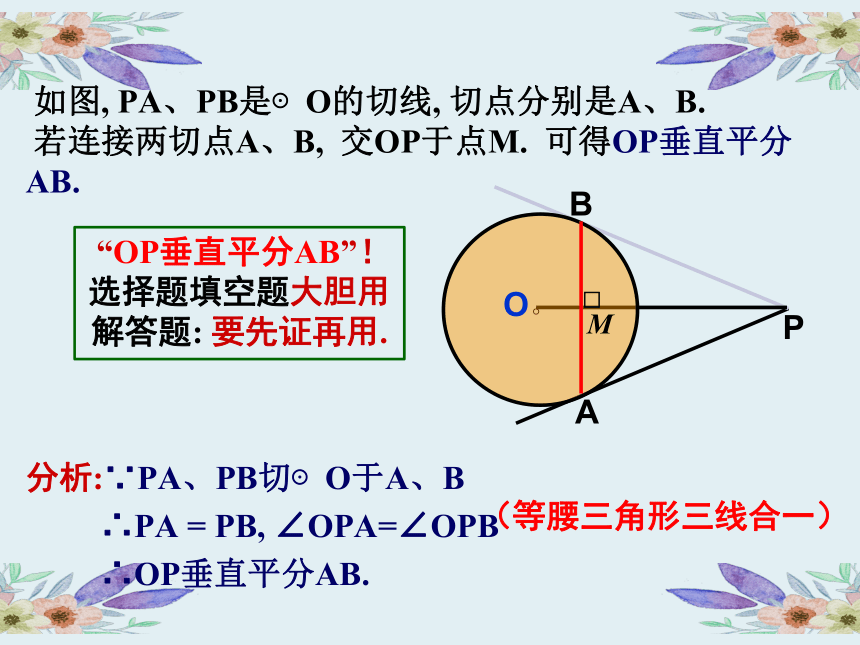
如图, PA、PB是⊙O的切线, 切点分别是A、B.
若连接两切点A、B, 交OP于点M. 可得OP垂直平分AB.
分析:∵PA、PB切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
∴OP垂直平分AB.
□
M
(等腰三角形三线合一)
“OP垂直平分AB”!
选择题填空题大胆用
解答题: 要先证再用.
问题二:如图是一张三角形的铁皮, 如何在它上面截下一块圆形的用料, 并且使圆的面积尽可能大呢?
·
A
B
C
与三角形各边都相切的圆面积最大.
思考:怎样确定这个圆的圆心与半径?
A
B
C
(2)三角形的内心就是三角形
的三个内角平分线的交点.
(3)三角形的内心到三角形
的三边的距离相等.
D
□
F
□
E
□
3. 三角形与内切圆的关系
O
(1)与三角形各边都相切的圆叫做三角形的内切圆;
三角形内切圆的圆心叫做三角形的内心.
思考:三角形的内心与外心有什么区别?
A
B
C
O
三角形的外接圆
三角形的内切圆
A
B
C
D
E
F
O
OA=OB=OC
OD=OE=OF
外心到各顶点
的距离相等.
内心到各边
的距离相等.
例1 如图,△ABC的内切圆⊙O与BC,CA, AB分别相切于点D,E,F,且AB=9, BC=14,CA=13.
(1)求AF,BD,CE的长.
(2)设⊙O的半径为2,求△ABC的面积
例2 如图,Rt△ABC中,∠C=900,AB,
BC,CA的长分别为c,a,b,求
△ABC 的内切圆半径 r.
例2:如图,?O为 的内切圆,切点分别为D、E、F, ,BC=4,AC=3.
(1)求AF的长
(2)求?O的半径
切线长定理:
从圆外一点引圆的两条切线, 它们的切线长相等, 圆心
和这一点的连线平分两条切线的夹角.
本课小结
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
(OP垂直平分AB)
★切线长定理的作用:
证明线段相等、线垂直, 角相等, 弧相等.
r
r
r
△ABC的内切圆半径为 r , △ABC的周长为 1,
求△ABC的面积.
(提示: 设内心为O, 连接OA、OB、OC.)
解: 连接OA、OB、OC, 则
能力提升
O
A
r
C
B
第24章 圆(12)
1.直线与圆有哪几种位置关系?
直线与圆位置关系: ①相离; ②相切; ③相交.
一、知识回顾:
2.切线的性质定理是什么?
圆的切线垂直于过切点的半径
问题一:
(1)过平面上一个已知点, 可以作已知圆的切线吗?
·O
·O
·O
P ·
P·
A
(2) 经过圆外一点P, 可以作已知⊙O的几条切线?
【问题】切线上的这点到切点之间的线段有什么性质?
二、问题导入:
P
·
·
O
P
B
1.切线长定义:
如图,过圆外一点P有两条直线PA、PB分别与⊙O相切.经过圆外一点的切线上, 这点和切点之间的线段的长叫做这点到圆的切线长.
A
二、新知探索
思考:连接OP
那么AP和BP有什么关系,∠APO和∠BPO?
为什么?
已知: 如图, PA、PB是⊙O的切线, 切点分别是A、B.
求证: PA=PB, ∠OPA=∠OPB.
证明:∵PA, PB与⊙O相切于A、B
∴OA⊥PA, OB⊥PB
则∠OAP=∠OBP=900
∵ OA=OB, OP=OP
∴Rt△AOP≌Rt△BOP (HL)
∴ PA = PB, ∠OPA=∠OPB.
A
P
O
。
B
应用格式:
∵PA、PB分别切⊙O于A、B
∴PA=PB, ∠OPA=∠OPB
2.切线长定理:
从圆外一点可以引圆的两条切线, 它们的切线长相等,
这点和圆心的连线平分两条切线的夹角.
A
P
O
。
B
。
A
B
P
O
如图, PA、PB是⊙O的切线, 切点分别是A、B.
若连接两切点A、B, 交OP于点M. 可得OP垂直平分AB.
分析:∵PA、PB切⊙O于A、B
∴PA = PB, ∠OPA=∠OPB
∴OP垂直平分AB.
□
M
(等腰三角形三线合一)
“OP垂直平分AB”!
选择题填空题大胆用
解答题: 要先证再用.
问题二:如图是一张三角形的铁皮, 如何在它上面截下一块圆形的用料, 并且使圆的面积尽可能大呢?
·
A
B
C
与三角形各边都相切的圆面积最大.
思考:怎样确定这个圆的圆心与半径?
A
B
C
(2)三角形的内心就是三角形
的三个内角平分线的交点.
(3)三角形的内心到三角形
的三边的距离相等.
D
□
F
□
E
□
3. 三角形与内切圆的关系
O
(1)与三角形各边都相切的圆叫做三角形的内切圆;
三角形内切圆的圆心叫做三角形的内心.
思考:三角形的内心与外心有什么区别?
A
B
C
O
三角形的外接圆
三角形的内切圆
A
B
C
D
E
F
O
OA=OB=OC
OD=OE=OF
外心到各顶点
的距离相等.
内心到各边
的距离相等.
例1 如图,△ABC的内切圆⊙O与BC,CA, AB分别相切于点D,E,F,且AB=9, BC=14,CA=13.
(1)求AF,BD,CE的长.
(2)设⊙O的半径为2,求△ABC的面积
例2 如图,Rt△ABC中,∠C=900,AB,
BC,CA的长分别为c,a,b,求
△ABC 的内切圆半径 r.
例2:如图,?O为 的内切圆,切点分别为D、E、F, ,BC=4,AC=3.
(1)求AF的长
(2)求?O的半径
切线长定理:
从圆外一点引圆的两条切线, 它们的切线长相等, 圆心
和这一点的连线平分两条切线的夹角.
本课小结
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
(OP垂直平分AB)
★切线长定理的作用:
证明线段相等、线垂直, 角相等, 弧相等.
r
r
r
△ABC的内切圆半径为 r , △ABC的周长为 1,
求△ABC的面积.
(提示: 设内心为O, 连接OA、OB、OC.)
解: 连接OA、OB、OC, 则
能力提升
O
A
r
C
B
同课章节目录
