北师大版九年级数学上册第四章4.5相似三角形判定定理的证明 同步测试(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册第四章4.5相似三角形判定定理的证明 同步测试(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-02 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学上册第四章
4.5相似三角形判定定理的证明
同步测试
一.
选择题
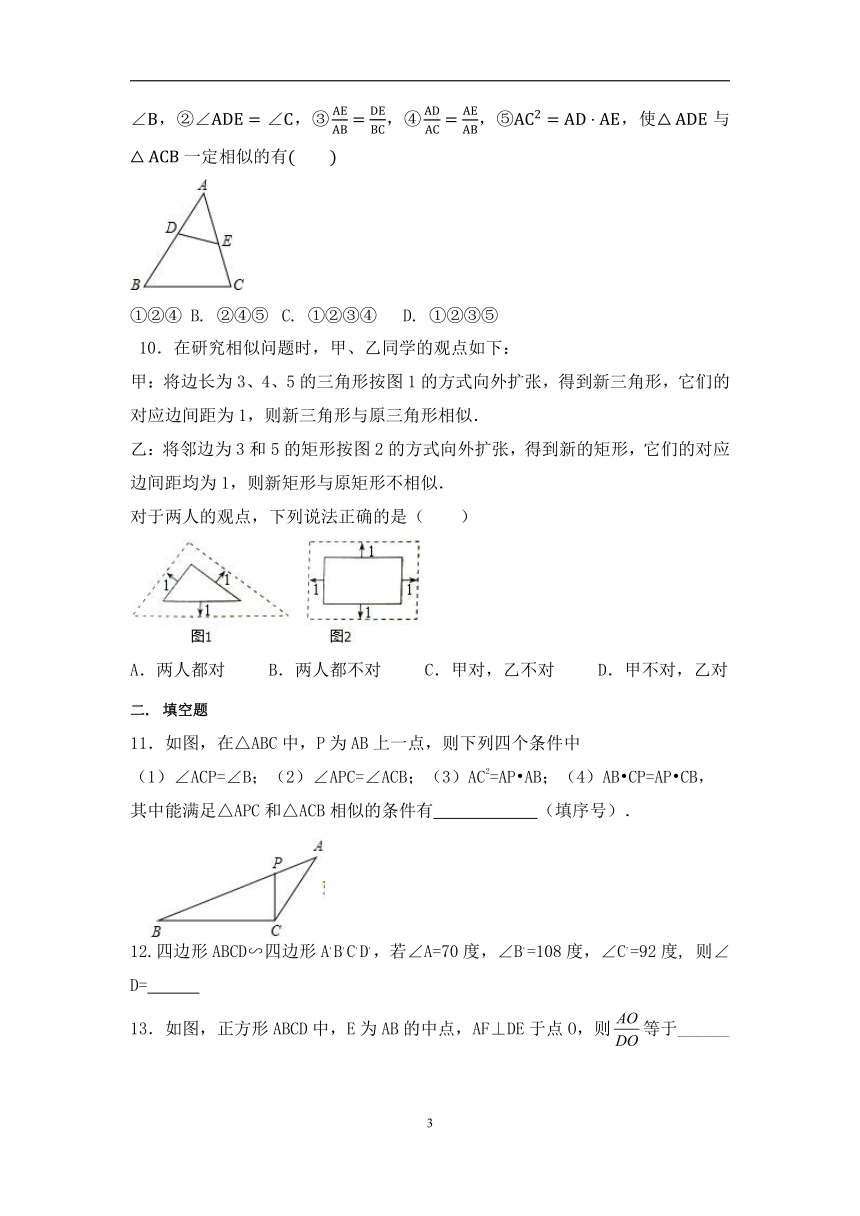
1.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A.B.C.D.
2.如图,在正三角形ABC中,D、E分别在AC、AB上,且=,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
3.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
D.
5.下面两个三角形一定相似的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个钝角三角形
D.两个等边三角形
6.如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处
B.3处
C.4处
D.5处
7.如图,在钝角三角形ABC中,,,动点D从A点出发到B点止,动点E从C点出发到A点止点D运动的速度为秒,点E运动的速度为秒如果两点同时运动,那么当以点A、D、E为顶点的三角形与相似时,运动的时间是
A.
4或
B.
3或
C.
2或4
D.
1或6
8.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1
B.2
C.3
D.4
9.如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:,,,,,使与一定相似的有
B.
C.
D.
10.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
二.
填空题
11.如图,在△ABC中,P为AB上一点,则下列四个条件中
(1)∠ACP=∠B;(2)∠APC=∠ACB;(3)AC2=AP?AB;(4)AB?CP=AP?CB,
其中能满足△APC和△ACB相似的条件有
(填序号).
12.四边形ABCD∽四边形A,B,C,D,,若∠A=70度,∠B,=108度,∠C,=92度,
则∠D=
13.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于______
14.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为
,可证明△AOB∽△DOC.
15.如图,在中,点E,F分别在AB,AC上,若∽,则需要增加的一个条件是______写出一个即可
16.如图,中,D、E分别是AB、AC边上一点,连接请你添加一个条件,使∽,则你添加的这一个条件可以是______写出一个即可.
如图所示,中,E,F分别是边AB,AC上的点,且满足,则与的面积比是______
.
18.如图,DE∥BC,EF∥AB,且S△ADE=4,S△EFC=9,则△ABC的面积为
三.解答题
19.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
求证:≌;??????
求证:∽.
20.如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F,如果∠EAC=∠D,试问:AC?BE与AE?CD是否相等?
21.如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
(1)求证:AC2=CE?CF;
(2)若∠B=38°,求∠CFD的度数.
22.如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
答案提示
1.B.2.B
3.C;4.D.5.D.6.C.7.
B
8.D.9.
A10.A.
11.(1)、(2)、(3).
12.∠D=900
13..
14.∠AOB=∠DOC;
15.
??16.
??17.
1:9?
18.25.?
19.
证明:正方形ABCD,等腰直角三角形EDF,
,,,
,
,
在和中,
,
≌;
延长BA到M,交ED于点M,
≌,
,即,
,
,
,
,
,
∽.??
20.解:∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵∠EAC=∠D,
∴∠EAC=∠B,
∵∠E=∠E,
∴△ACE∽△BAE,
∴AC:AE=AB:BE,
即AC?BE=AE?AB,
∵AB=CD,
∴AC?BE=AE?CD.
21.解:(1)∵AD⊥BC,
∴∠CFA=90°,
∵∠BAC=90°,
∴∠CFA=∠BAC,
∵∠ACF=∠FCA,
∴△CAF∽△CEA,
∴,
∴CA2=CE?CF;
(2)∵∠CAB=∠CDA,∠ACD=∠BCA,
∴△CAD∽△CBA,
∴,
∴CA2=CB×CD,
同理可得:CA2=CF×CE,
∴CD?BC=CF?CE,
∴,
∵∠DCF=∠ECB,
∴△CDF∽△CEB,
∴∠CFD=∠B,
∵∠B=38°,
∴∠CFD=38°.
22.解:设经过t秒时,以△QBC与△ABC相似,则AP=2t,BP=8-2t,BQ=4t,
∵∠PBQ=∠ABC,
∴当时,△BPQ∽△BAC,
即,解得t=2(s);
当时,△BPQ∽△BCA,
即,解得t=0.8(s);
综合上述,经过2秒或0.8秒时,△QBC与△ABC相似.
4.5相似三角形判定定理的证明
同步测试
一.
选择题
1.如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A.B.C.D.
2.如图,在正三角形ABC中,D、E分别在AC、AB上,且=,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
3.如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
D.
5.下面两个三角形一定相似的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个钝角三角形
D.两个等边三角形
6.如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处
B.3处
C.4处
D.5处
7.如图,在钝角三角形ABC中,,,动点D从A点出发到B点止,动点E从C点出发到A点止点D运动的速度为秒,点E运动的速度为秒如果两点同时运动,那么当以点A、D、E为顶点的三角形与相似时,运动的时间是
A.
4或
B.
3或
C.
2或4
D.
1或6
8.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1
B.2
C.3
D.4
9.如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:,,,,,使与一定相似的有
B.
C.
D.
10.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
二.
填空题
11.如图,在△ABC中,P为AB上一点,则下列四个条件中
(1)∠ACP=∠B;(2)∠APC=∠ACB;(3)AC2=AP?AB;(4)AB?CP=AP?CB,
其中能满足△APC和△ACB相似的条件有
(填序号).
12.四边形ABCD∽四边形A,B,C,D,,若∠A=70度,∠B,=108度,∠C,=92度,
则∠D=
13.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于______
14.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为
,可证明△AOB∽△DOC.
15.如图,在中,点E,F分别在AB,AC上,若∽,则需要增加的一个条件是______写出一个即可
16.如图,中,D、E分别是AB、AC边上一点,连接请你添加一个条件,使∽,则你添加的这一个条件可以是______写出一个即可.
如图所示,中,E,F分别是边AB,AC上的点,且满足,则与的面积比是______
.
18.如图,DE∥BC,EF∥AB,且S△ADE=4,S△EFC=9,则△ABC的面积为
三.解答题
19.如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
求证:≌;??????
求证:∽.
20.如图,ABCD是平行四边形,点E在边BC延长线上,连AE交CD于点F,如果∠EAC=∠D,试问:AC?BE与AE?CD是否相等?
21.如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
(1)求证:AC2=CE?CF;
(2)若∠B=38°,求∠CFD的度数.
22.如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
答案提示
1.B.2.B
3.C;4.D.5.D.6.C.7.
B
8.D.9.
A10.A.
11.(1)、(2)、(3).
12.∠D=900
13..
14.∠AOB=∠DOC;
15.
??16.
??17.
1:9?
18.25.?
19.
证明:正方形ABCD,等腰直角三角形EDF,
,,,
,
,
在和中,
,
≌;
延长BA到M,交ED于点M,
≌,
,即,
,
,
,
,
,
∽.??
20.解:∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵∠EAC=∠D,
∴∠EAC=∠B,
∵∠E=∠E,
∴△ACE∽△BAE,
∴AC:AE=AB:BE,
即AC?BE=AE?AB,
∵AB=CD,
∴AC?BE=AE?CD.
21.解:(1)∵AD⊥BC,
∴∠CFA=90°,
∵∠BAC=90°,
∴∠CFA=∠BAC,
∵∠ACF=∠FCA,
∴△CAF∽△CEA,
∴,
∴CA2=CE?CF;
(2)∵∠CAB=∠CDA,∠ACD=∠BCA,
∴△CAD∽△CBA,
∴,
∴CA2=CB×CD,
同理可得:CA2=CF×CE,
∴CD?BC=CF?CE,
∴,
∵∠DCF=∠ECB,
∴△CDF∽△CEB,
∴∠CFD=∠B,
∵∠B=38°,
∴∠CFD=38°.
22.解:设经过t秒时,以△QBC与△ABC相似,则AP=2t,BP=8-2t,BQ=4t,
∵∠PBQ=∠ABC,
∴当时,△BPQ∽△BAC,
即,解得t=2(s);
当时,△BPQ∽△BCA,
即,解得t=0.8(s);
综合上述,经过2秒或0.8秒时,△QBC与△ABC相似.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
