人教版八年级数学上册13.3.2等边三角形课件(共31张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.2等边三角形课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 19:33:53 | ||
图片预览










文档简介
(共31张PPT)
13.3.2等边三角形
如图
△ABC中AB=AC
等腰三角形的性质:
1、等腰三角形两底角相等(等边对等角),
2、等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(三线合一)。
D
C
B
A
3、等腰三角形是轴对称图形.对称轴______________所在直线.
O
A
B
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
∴OA=OB
(等角对等边
)
∵
△ABC中,
∠A=?B
等腰三角形的判定
O
A
B
C
M
N
角平分线+平行
等腰三角形
1
2
3
三边都相等的三角形叫等边三角形。等边三角形是特殊的等腰三角形。也叫正三角形。
探索新知
A
B
C
AB=BC=CA
提出问题:等边三角形有哪些特殊的性质呢?
根据等腰三角形的性质去探讨等边三角形的性质:
①从边看;②从角看;③从对称性看;④从重要线段看
A
B
C
等边三角形的内角都相等吗?为什么?
探究一
由已知:AB=AC=BC,
∵AB=AC,
∴∠B=∠C.
同理
∠A=∠C,
∴∠A=∠B=∠C.
∵
∠A+∠B+∠C=180°,
∴
∠A=
∠B=
∠C=60
°
.
等边三角形有“三线合一”的性质吗?为什么?
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探究性质二
等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.
等边三角形性质探索三:
(对称轴是等边三角形的高或角平线或中线所在的直线)
⑵ 等边三角形的三个内角都相等,并且
每一个角都等于60°.
等边三角形的性质
⑴ 等边三角形的三边都相等
A
B
C
)
(
60°
60°
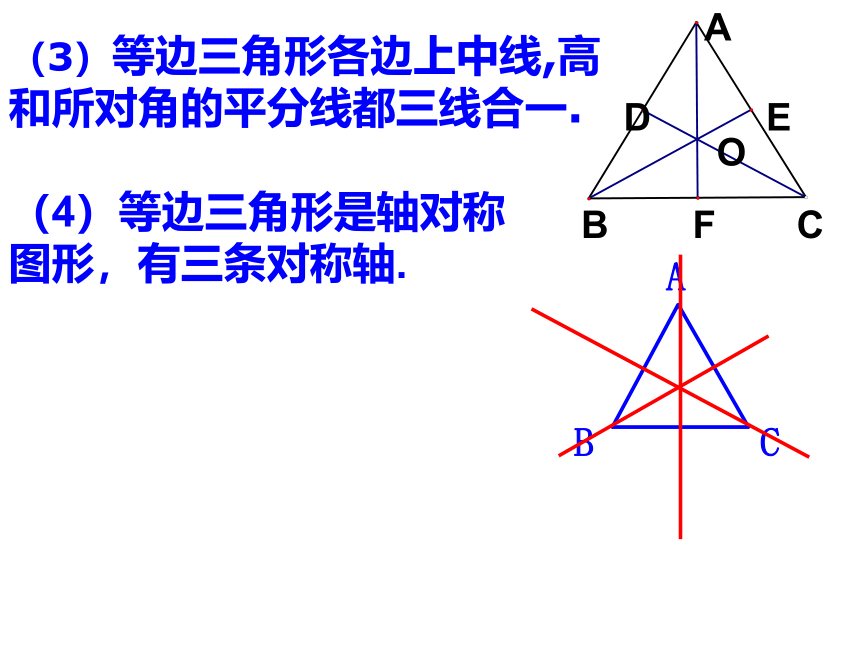
(3)等边三角形各边上中线,高和所对角的平分线都三线合一.
(4)等边三角形是轴对称图形,有三条对称轴.
A
F
E
D
C
B
O
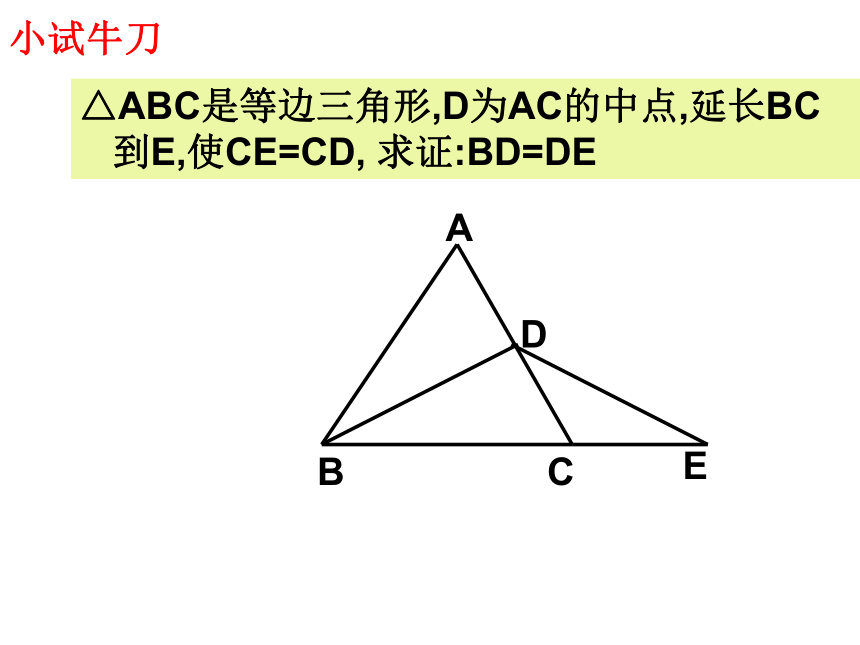
△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
小试牛刀
△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
证明:∵
△ABC是等边三角形
∴
AB=AC=BC,
∠ABC=
∠A=
∠ACB=
60°
∴
∠DBC=
∠E
∴BD=DE
(等角对等边)
∵
CE=CD
∴
∠CDE=
∠E=1/2
∠ACB=
30°
(等边对等角)
∵
AB=AC,D为AC的中点
∴
∠ABD=
∠DBC=1/2
∠ABC=
30°(三线合一
)
思考题
?
一个三角形满足什么条件
就是等边三角形?
三个角都相等的三角形是等边三角形?
已知:如图,⊿ABC中,
∠
A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵
∠
A=∠B(已知)
∴BC=CA(等角对等边)
同理
CA=AB
∴BC=CA=AB
A
B
C
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
推论1:三个角都相等的三角形是等边三角形。
如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
已知:
⊿ABC中,AB=AC,
∠
A=600。
求证:AB=AC=BC
A
B
C
证明:
⊿ABC中
∵AB=AC,
∴
∠B=∠C
(等边对等角)
∵
∠
A=600
∴
∠B=∠C
=
600
∴AB=AC=BC(等角对等边)
推论2:
有一个角是
60°的等腰三角形是等边三角形。
A
B
C
∵
∠B=600
AB=BC
∴△ABC是等边三角形
2.
三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵
∠B=600
AB=BC
∴△ABC是等边三角形
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
等边三角形的判定方法
等边三角形与等腰三角形异同
定义
性质
判定
等腰
三角形
等边
三角形
有两条边相等
①两边、两角相等
②三线合一
③一条对称轴
①三边、三角相等
②三线合一
③三条对称轴
有三条边相等
①定义
②等角对等边
①定义
②三个角都相等
③等腰三角形有一
个角是60°
例1
如图,课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便得出了一个结论:池塘最长处不小于200m.他们的结论对吗?
解:在△APB中,AP=BP,
∠APB=60°,
所以∠PAB=
∠PBA=1/2(180°-∠APB)
=1/2(180°-60°)
=60°
于是
∠PAB=
∠PBA=
∠APB
从而△APB是等边三角形,AB的长是200m.由此可以得出兴趣小组的结论是正确的.
例2.如图,在等边三角形ABC的边AB、AC上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。
A
B
C
D
E
你还有其它方法
使△ADE是等边三
角形吗?
可添加的条件为:AD=AE,BD=CE;
∠ADE=60°;∠ADE=
∠ABC;
DE∥BC等.
练习一:
如图,等边三角形ABC中,AD是BC上的高,∠BDE=
∠CDF=60°,结合图形,你能得出那些结论?
结论:
线:BD=DC=BE=DE=DF=CF
=AF=AE
角:∠ADE=
∠ADF=
∠EAD=
∠DAF=
30°
形:△ADE和△ADF是等腰三角形
△BED和△CFD是等边三角形
其他:DE∥AC,DF∥AB等.
A
C
B
D
E
F
如图,等边三角形ABC中,AD是BC上的高,延长AB到点E,使BE=BD,连接DE,则△ADE的形状是____________.
等腰三角形
E
D
C
A
B
练习二
如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF。
试问:△DEF是什么三角形?
A
B
C
D
E
F
练习三
如图,P、Q是△ABC的边BC上的两点,
并PB=PQ=QC=AP=AQ,则∠BAC的大
小为______.
A
B
P
Q
C
120°
练习四
练习与巩固
1.下列说法中,正确说法的个数为(
)
(1)若等腰三角形有一个角等于60°,则这个三角形为等边三角形
(2)等边三角形一定是等腰三角形,而等腰三角形不一定是等边三角形
(3)有两个角是60°的三角形一定是等三角形
(4)等边三角形中所有的中线、高、角平分线总条数是3条
A.1个
B.2个
C.3个
D.4个
D
2.如果一个三角形是轴对称图形,且有一个外角是120°,那么这个三角形是(
)
A.直角三角形
B.等腰直角三角形
C.正三角形
D.含30°角的直角三角形
3.如图,△ABC是等边三角形,且∠1=∠2=∠3,则∠D等于(
)
A.90°
B.80
°
C.45°
D.60°
A
B
C
D
E
F
1
2
3
C
D
小结
我们这节课学习了哪些知识?
谈谈你的体会.
13.3.2等边三角形
如图
△ABC中AB=AC
等腰三角形的性质:
1、等腰三角形两底角相等(等边对等角),
2、等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(三线合一)。
D
C
B
A
3、等腰三角形是轴对称图形.对称轴______________所在直线.
O
A
B
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
∴OA=OB
(等角对等边
)
∵
△ABC中,
∠A=?B
等腰三角形的判定
O
A
B
C
M
N
角平分线+平行
等腰三角形
1
2
3
三边都相等的三角形叫等边三角形。等边三角形是特殊的等腰三角形。也叫正三角形。
探索新知
A
B
C
AB=BC=CA
提出问题:等边三角形有哪些特殊的性质呢?
根据等腰三角形的性质去探讨等边三角形的性质:
①从边看;②从角看;③从对称性看;④从重要线段看
A
B
C
等边三角形的内角都相等吗?为什么?
探究一
由已知:AB=AC=BC,
∵AB=AC,
∴∠B=∠C.
同理
∠A=∠C,
∴∠A=∠B=∠C.
∵
∠A+∠B+∠C=180°,
∴
∠A=
∠B=
∠C=60
°
.
等边三角形有“三线合一”的性质吗?为什么?
结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。
探究性质二
等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.
等边三角形性质探索三:
(对称轴是等边三角形的高或角平线或中线所在的直线)
⑵ 等边三角形的三个内角都相等,并且
每一个角都等于60°.
等边三角形的性质
⑴ 等边三角形的三边都相等
A
B
C
)
(
60°
60°
(3)等边三角形各边上中线,高和所对角的平分线都三线合一.
(4)等边三角形是轴对称图形,有三条对称轴.
A
F
E
D
C
B
O
△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
小试牛刀
△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
证明:∵
△ABC是等边三角形
∴
AB=AC=BC,
∠ABC=
∠A=
∠ACB=
60°
∴
∠DBC=
∠E
∴BD=DE
(等角对等边)
∵
CE=CD
∴
∠CDE=
∠E=1/2
∠ACB=
30°
(等边对等角)
∵
AB=AC,D为AC的中点
∴
∠ABD=
∠DBC=1/2
∠ABC=
30°(三线合一
)
思考题
?
一个三角形满足什么条件
就是等边三角形?
三个角都相等的三角形是等边三角形?
已知:如图,⊿ABC中,
∠
A=∠B=∠C
求证:AB=AC=BC
A
B
C
证明:在⊿ABC中
∵
∠
A=∠B(已知)
∴BC=CA(等角对等边)
同理
CA=AB
∴BC=CA=AB
A
B
C
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
推论1:三个角都相等的三角形是等边三角形。
如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?
第一种情况:当顶角是60度时
第二种情况:当底角是60度时
已知:
⊿ABC中,AB=AC,
∠
A=600。
求证:AB=AC=BC
A
B
C
证明:
⊿ABC中
∵AB=AC,
∴
∠B=∠C
(等边对等角)
∵
∠
A=600
∴
∠B=∠C
=
600
∴AB=AC=BC(等角对等边)
推论2:
有一个角是
60°的等腰三角形是等边三角形。
A
B
C
∵
∠B=600
AB=BC
∴△ABC是等边三角形
2.
三个角都相等的三角形是等边三角形.
3.有一个角是60°的等腰三角形是等边三角形.
1.三边都相等的三角形是等边三角形.(定义)
一般三角形
等边三角形
A
B
C
等腰三角形
等边三角形
A
B
C
∵AB=BC=AC
∴△ABC是等边三角形
∵
∠B=600
AB=BC
∴△ABC是等边三角形
∵
∠A=
∠
B=
∠
C
∴△ABC是等边三角形
等边三角形的判定方法
等边三角形与等腰三角形异同
定义
性质
判定
等腰
三角形
等边
三角形
有两条边相等
①两边、两角相等
②三线合一
③一条对称轴
①三边、三角相等
②三线合一
③三条对称轴
有三条边相等
①定义
②等角对等边
①定义
②三个角都相等
③等腰三角形有一
个角是60°
例1
如图,课外兴趣小组在一次测量活动中,测得∠APB=60°,AP=BP=200m,他们便得出了一个结论:池塘最长处不小于200m.他们的结论对吗?
解:在△APB中,AP=BP,
∠APB=60°,
所以∠PAB=
∠PBA=1/2(180°-∠APB)
=1/2(180°-60°)
=60°
于是
∠PAB=
∠PBA=
∠APB
从而△APB是等边三角形,AB的长是200m.由此可以得出兴趣小组的结论是正确的.
例2.如图,在等边三角形ABC的边AB、AC上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。
A
B
C
D
E
你还有其它方法
使△ADE是等边三
角形吗?
可添加的条件为:AD=AE,BD=CE;
∠ADE=60°;∠ADE=
∠ABC;
DE∥BC等.
练习一:
如图,等边三角形ABC中,AD是BC上的高,∠BDE=
∠CDF=60°,结合图形,你能得出那些结论?
结论:
线:BD=DC=BE=DE=DF=CF
=AF=AE
角:∠ADE=
∠ADF=
∠EAD=
∠DAF=
30°
形:△ADE和△ADF是等腰三角形
△BED和△CFD是等边三角形
其他:DE∥AC,DF∥AB等.
A
C
B
D
E
F
如图,等边三角形ABC中,AD是BC上的高,延长AB到点E,使BE=BD,连接DE,则△ADE的形状是____________.
等腰三角形
E
D
C
A
B
练习二
如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF。
试问:△DEF是什么三角形?
A
B
C
D
E
F
练习三
如图,P、Q是△ABC的边BC上的两点,
并PB=PQ=QC=AP=AQ,则∠BAC的大
小为______.
A
B
P
Q
C
120°
练习四
练习与巩固
1.下列说法中,正确说法的个数为(
)
(1)若等腰三角形有一个角等于60°,则这个三角形为等边三角形
(2)等边三角形一定是等腰三角形,而等腰三角形不一定是等边三角形
(3)有两个角是60°的三角形一定是等三角形
(4)等边三角形中所有的中线、高、角平分线总条数是3条
A.1个
B.2个
C.3个
D.4个
D
2.如果一个三角形是轴对称图形,且有一个外角是120°,那么这个三角形是(
)
A.直角三角形
B.等腰直角三角形
C.正三角形
D.含30°角的直角三角形
3.如图,△ABC是等边三角形,且∠1=∠2=∠3,则∠D等于(
)
A.90°
B.80
°
C.45°
D.60°
A
B
C
D
E
F
1
2
3
C
D
小结
我们这节课学习了哪些知识?
谈谈你的体会.
