3.4.2 数据的离散程度同步练习题(含答案)
文档属性
| 名称 | 3.4.2 数据的离散程度同步练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 14:17:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 数据的分析
4 数据的离散程度
第2课时
考点突破
考点 方差的应用
例 为改良玉米种植品种,某实验员从甲、乙两种玉米苗中各抽取10株进行初期研究,分别测得株高如下(单位:cm):
甲: 25,41,40,37,22,14, 19,39,21, 42;
乙: 27,16,44,27,44,16, 40,40,16, 40.
问:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
思路导引: 由于平均数、极差和方差,分别反映玉米苗长的平均水平和稳定情况,因此从不同的需求出发,就有不同的方案。
方法归纳
1,长得高和长得齐是两个不同的概念,注意区分,前者用平均数来反映,后者则用方差来反映。
2,用方差比较数据稳定性的一般步骤:
(1)找数据>根据实际问题,找出问题中的相关数据;
(2)求方差:利用方差公式,求得每一组数据的方差;
(3)得结论:根据方差的特征,得出数据的稳定性。
题组训练
1.甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄方差分别是涌=27,=19.6,=1.6.导游小王最喜欢带游客年龄相近的团队,若在三个团队中选择一个,则他应选( )
A.甲团 B.乙团 C.丙团 D.甲或乙团
2,(河南)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
差 3.6 3.6 7.4 8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
3,甲、乙两台机床生产同一种零件,并且每天产量相等,在6天里每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2, 1,0,2,则甲、乙两台机床中性能较稳定的是__________。
4,班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛,在最近的10次选拔赛中,他们的成绩如下(单位:cm).
甲 585 596 610 598 612 597 604 600 613 601
乙 613 618 580 574 618 593 585 590 598 624
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的方差是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
巩固练习
1.(衡阳)要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A.平均数 B.中位数 C众数 D.方差
2,(永州)在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9,8,8 乙:7、9.6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8 B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6 D.甲得分的方差比乙得分的方差小
3,甲、乙两名运动员在相同的条件下各射靶10次,每次射靶的成绩情况如下图所示:
(1)请你根据图中数据填写下表:
运动员 平均数 中位数 方差
甲 7 7
乙 7
2.6
(2)根据以上信息分析谁的成绩好些.
4. (☆)为了了解市场上甲、乙两种手表日走时误差的情况,从这两种手表中各随机抽取10块进行测试,两种手表日走时误差的数据如下(单位:秒):
甲种手表: -3,4,2,-1,-2,-2,1,-2,2,1;
乙种手表: -4,2,-3,2,4,2,-3,-1,4,-3.
根据所学方差知识,请你判断哪种手表走时稳定性好?
5. 学校篮球队五名队员的年龄分别为17,15,17, 16, 15(岁),其方差为0.8,则三年后这五名队员年龄的方差为___________。
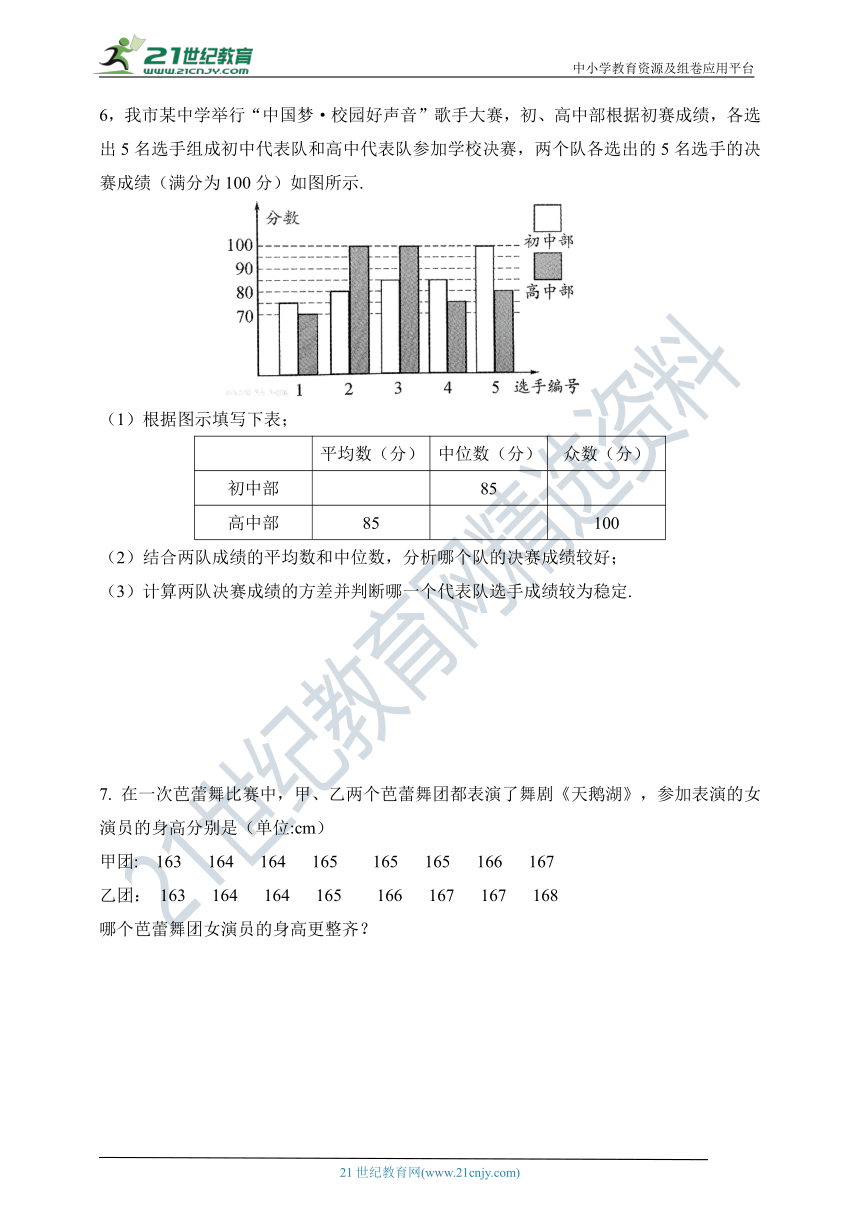
6,我市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
平均数(分) 中位数(分) 众数(分)
初中部
85
高中部 85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
7. 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高分别是(单位:cm)
甲团: 163 164 164 165 165 165 166 167
乙团: 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐?
8,(河北)某厂生产A, B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价的变化情况,绘制了如下统计表及不完整的折线图:
第一次 第二次 第三次
A产品单价(元/件 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
=5.9;=[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]÷3=.
(1)补全图中B产品单价变化的折线图. B产品第三次的单价比上一次的单价降低了_______%;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件, B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
参考答案
考点突破
例 解:(1)=(25+41+…+42)÷10=30(cm) ;
=(27+16+…+40)÷10=31(cm).
∵<,∴乙玉米苗长得高.
(2)=[(25-30)2+ (41-30)2+…+(42-30)2]÷10=104.2,
=[(27-31)2+(16-31)2+…+(40-31)2]÷10=128.8.
∴<,∴甲玉米苗长得齐.
题组训练
C 2. A 3. 乙
4,解:(1)甲的平均数为(585+596+…+601)÷10 =601.6;
乙的平均数为(613+618+…+624)÷10 =599. 3.
(2)=[(585-601.6)2+(596-601.6)2+…+(601-601.6)2]÷10=59.04;
=[(613 -599 .3)2+(618-599.3)2+…+(624-599.3)2]÷10=284. 21.
(3)甲的成绩较稳定,乙的最好成绩好.
(4)若只想夺冠,选甲参加比赛;若要打破记录,应选乙参加比赛.
巩固练习
D 2. C
3,解:(1)=1,乙的中位数为7.
(2)因为甲、乙的平均数与中位数都相同,甲的方差小,所以更稳定,因此甲的成绩好些.
4,解:=(-3+4+2-1-2-2+1-2+2-1)÷10=0,
=[(-3)2+42+…+12]=;
=(-4+2-3+2+4+2-3-1+4-3)÷10=0,
=[(-4)2+22+…+(-3)2]=。
显然<,所以甲种手表走时稳定性好.
0.8
6,解: (1)填表:初中部平均数为85 (分),众数为85 (分);高中部中位数为80(分).
(2)初中部成绩好些.因为两个队的平均数都相同,初中部的中位数高,所以在平均数相同的情况下中位数高的初中部成绩好些.
(3)=[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]÷5=70,
=[(70-85)2+(100-85)2+(100-85)2+(75+85)2+(80+85)2]÷5=160。∴<。
因此,初中代表队选手成绩较为稳定.
7,解:甲、乙两团女演员的平均身高分别是
=(163+164×2+165×3+166+167)÷8=164. 875(cm),
=(163+164×2+165+166+167×2+168)÷8=165.5(cm),
则=[(163-164. 875)2+(164-164. 875)2+…+(167-164.875)2]÷8≈1.36,
=[(163-165. 5)2 +(164-165.5)2+…+(168-165. 5)2]÷8=2. 75.
由<,可知甲芭蕾舞团女演员的身高更整齐.
8.解:(1)如图所示
25
(2)=(3.5+4+3)÷3=3.5;
=[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]÷3=.
∵,∴B产品的单价波动小。
(3)第四次调价厚朴对于A产品,这四次单价的中位数为;
对于B产品,∵m>0,∴第四次单价大于3。
又∵,∴第四次单价小于4.
∴。∴m=25。
_21?????????è?????(www.21cnjy.com)_
第三章 数据的分析
4 数据的离散程度
第2课时
考点突破
考点 方差的应用
例 为改良玉米种植品种,某实验员从甲、乙两种玉米苗中各抽取10株进行初期研究,分别测得株高如下(单位:cm):
甲: 25,41,40,37,22,14, 19,39,21, 42;
乙: 27,16,44,27,44,16, 40,40,16, 40.
问:(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
思路导引: 由于平均数、极差和方差,分别反映玉米苗长的平均水平和稳定情况,因此从不同的需求出发,就有不同的方案。
方法归纳
1,长得高和长得齐是两个不同的概念,注意区分,前者用平均数来反映,后者则用方差来反映。
2,用方差比较数据稳定性的一般步骤:
(1)找数据>根据实际问题,找出问题中的相关数据;
(2)求方差:利用方差公式,求得每一组数据的方差;
(3)得结论:根据方差的特征,得出数据的稳定性。
题组训练
1.甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄方差分别是涌=27,=19.6,=1.6.导游小王最喜欢带游客年龄相近的团队,若在三个团队中选择一个,则他应选( )
A.甲团 B.乙团 C.丙团 D.甲或乙团
2,(河南)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
差 3.6 3.6 7.4 8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
3,甲、乙两台机床生产同一种零件,并且每天产量相等,在6天里每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2, 1,0,2,则甲、乙两台机床中性能较稳定的是__________。
4,班主任要从甲、乙两名跳远运动员中挑选一人参加校运动会比赛,在最近的10次选拔赛中,他们的成绩如下(单位:cm).
甲 585 596 610 598 612 597 604 600 613 601
乙 613 618 580 574 618 593 585 590 598 624
(1)他们的平均成绩分别是多少?
(2)甲、乙两名运动员这10次比赛成绩的方差是多少?
(3)怎样评价这两名运动员的运动成绩?
(4)历届比赛表明,成绩达到5.96m就有可能夺冠,你认为为了夺冠应选择谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破记录,那么你认为为了打破记录应选择谁参加这项比赛?
巩固练习
1.(衡阳)要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A.平均数 B.中位数 C众数 D.方差
2,(永州)在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9,8,8 乙:7、9.6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8 B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6 D.甲得分的方差比乙得分的方差小
3,甲、乙两名运动员在相同的条件下各射靶10次,每次射靶的成绩情况如下图所示:
(1)请你根据图中数据填写下表:
运动员 平均数 中位数 方差
甲 7 7
乙 7
2.6
(2)根据以上信息分析谁的成绩好些.
4. (☆)为了了解市场上甲、乙两种手表日走时误差的情况,从这两种手表中各随机抽取10块进行测试,两种手表日走时误差的数据如下(单位:秒):
甲种手表: -3,4,2,-1,-2,-2,1,-2,2,1;
乙种手表: -4,2,-3,2,4,2,-3,-1,4,-3.
根据所学方差知识,请你判断哪种手表走时稳定性好?
5. 学校篮球队五名队员的年龄分别为17,15,17, 16, 15(岁),其方差为0.8,则三年后这五名队员年龄的方差为___________。
6,我市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
平均数(分) 中位数(分) 众数(分)
初中部
85
高中部 85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
7. 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高分别是(单位:cm)
甲团: 163 164 164 165 165 165 166 167
乙团: 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐?
8,(河北)某厂生产A, B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价的变化情况,绘制了如下统计表及不完整的折线图:
第一次 第二次 第三次
A产品单价(元/件 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
=5.9;=[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]÷3=.
(1)补全图中B产品单价变化的折线图. B产品第三次的单价比上一次的单价降低了_______%;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件, B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
参考答案
考点突破
例 解:(1)=(25+41+…+42)÷10=30(cm) ;
=(27+16+…+40)÷10=31(cm).
∵<,∴乙玉米苗长得高.
(2)=[(25-30)2+ (41-30)2+…+(42-30)2]÷10=104.2,
=[(27-31)2+(16-31)2+…+(40-31)2]÷10=128.8.
∴<,∴甲玉米苗长得齐.
题组训练
C 2. A 3. 乙
4,解:(1)甲的平均数为(585+596+…+601)÷10 =601.6;
乙的平均数为(613+618+…+624)÷10 =599. 3.
(2)=[(585-601.6)2+(596-601.6)2+…+(601-601.6)2]÷10=59.04;
=[(613 -599 .3)2+(618-599.3)2+…+(624-599.3)2]÷10=284. 21.
(3)甲的成绩较稳定,乙的最好成绩好.
(4)若只想夺冠,选甲参加比赛;若要打破记录,应选乙参加比赛.
巩固练习
D 2. C
3,解:(1)=1,乙的中位数为7.
(2)因为甲、乙的平均数与中位数都相同,甲的方差小,所以更稳定,因此甲的成绩好些.
4,解:=(-3+4+2-1-2-2+1-2+2-1)÷10=0,
=[(-3)2+42+…+12]=;
=(-4+2-3+2+4+2-3-1+4-3)÷10=0,
=[(-4)2+22+…+(-3)2]=。
显然<,所以甲种手表走时稳定性好.
0.8
6,解: (1)填表:初中部平均数为85 (分),众数为85 (分);高中部中位数为80(分).
(2)初中部成绩好些.因为两个队的平均数都相同,初中部的中位数高,所以在平均数相同的情况下中位数高的初中部成绩好些.
(3)=[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]÷5=70,
=[(70-85)2+(100-85)2+(100-85)2+(75+85)2+(80+85)2]÷5=160。∴<。
因此,初中代表队选手成绩较为稳定.
7,解:甲、乙两团女演员的平均身高分别是
=(163+164×2+165×3+166+167)÷8=164. 875(cm),
=(163+164×2+165+166+167×2+168)÷8=165.5(cm),
则=[(163-164. 875)2+(164-164. 875)2+…+(167-164.875)2]÷8≈1.36,
=[(163-165. 5)2 +(164-165.5)2+…+(168-165. 5)2]÷8=2. 75.
由<,可知甲芭蕾舞团女演员的身高更整齐.
8.解:(1)如图所示
25
(2)=(3.5+4+3)÷3=3.5;
=[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]÷3=.
∵,∴B产品的单价波动小。
(3)第四次调价厚朴对于A产品,这四次单价的中位数为;
对于B产品,∵m>0,∴第四次单价大于3。
又∵,∴第四次单价小于4.
∴。∴m=25。
_21?????????è?????(www.21cnjy.com)_
