高一物理人教版必修1学案 4.3 牛顿第二定律 Word版含解析
文档属性
| 名称 | 高一物理人教版必修1学案 4.3 牛顿第二定律 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 654.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览



文档简介
3 牛顿第二定律
【例1】 (多选)下列对牛顿第二定律的表达式F=ma及其变形公式的理解,正确的是( )
A.由F=ma可知,物体所受的合力与物体的质量成正比,与物体的加速度成反比
B.由m=可知,物体的质量与其所受的合力成正比,与其运动的加速度成反比
C.由a=可知,物体的加速度与其所受的合力成正比,与其质量成反比
D.由m=可知,物体的质量可以通过测量它的加速度和它所受的合力而求出
解答本题时应把握以下两点:
(1)物体的加速度决定于物体所受的合力和物体的质量.
(2)物体的质量决定于物体本身.
【解析】 牛顿第二定律的表达式F=ma表明了各物理量之间的数量关系,即已知两个量,可以求第三个量;物体的质量由物体本身决定,与受力无关;物体所受的合力,是由和它相互作用的物体共同产生的,与物体的质量和加速度无关;而由a=可知,物体的加速度与所受合外力成正比,与其质量成反比.综上分析知,选项A、B错误,C、D正确.
【答案】 CD
总结提能 a=是加速度的决定式,故a与F成正比,与m成反比,由其变形公式m=可以求解物体的质量,但不能认为m与F成正比,与a成反比.
一物体在多个力的作用下处于静止状态,如果仅使其中某个力的大小逐渐减小到零,然后又逐渐从零恢复到原来大小,在上述过程中,此力的方向一直保持不变,那么如图所示的v-t图象中,可能符合此过程中物体运动情况的是( D )
解析:其中的一个力逐渐减小到零的过程中,物体受到的合力逐渐增大,则其加速度逐渐增大,速度时间图象中图线的斜率表示加速度,所以在力逐渐减小到零的过程中,图线的斜率的绝对值逐渐增大,当这个力又从零恢复到原来大小时,合力逐渐减小,加速度逐渐减小,图线斜率的绝对值逐渐减小,只有D符合题意.
考点二 正交分解法在牛顿第二定律解题中的应用
正交分解法是把一个矢量分解在两个互相垂直的坐标轴上的方法,是一种常用的矢量运算方法.其实质是将复杂的矢量运算转化为简单的代数运算,从而简捷方便地解题,是解牛顿第二定律问题的基本方法.物体在受到三个或三个以上的力的作用时,一般都用正交分解法.
表示方法
为减少矢量的分解,在建立正交坐标系时,应使尽可能多的矢量落在两个坐标轴上,因此,确定x轴正方向有两种方法.
(1)分解力而不分解加速度:通常以加速度的方向为x轴的正方向,建立正交坐标系,将物体所受的各个力分解到x轴和y轴上,分别得x轴和y轴上的合力Fx和Fy,根据力的独立作用原理列方程组
(2)分解加速度而不分解力:若物体受几个相互垂直的力的作用,应用牛顿定律求解时,如果仍分解力就比较烦琐,所以在建立正交坐标系时,可根据物体的受力情况,以某个力的方向为x轴的正方向,使尽可能多的力落在坐标轴上而分解加速度a,得ax和ay,根据牛顿第二定律列方程组
温馨提示:正交分解建立坐标系的原则:
(1)一般情况:以加速度的方向为一个坐标轴的正方向,垂直于加速度的方向为另一坐标轴的方向.
(2)特殊情况:所有力都在两个互相垂直的方向上,而加速度不在这两个方向上,建立坐标系时应使各个力都在坐标轴上,即分解加速度而不分解力.
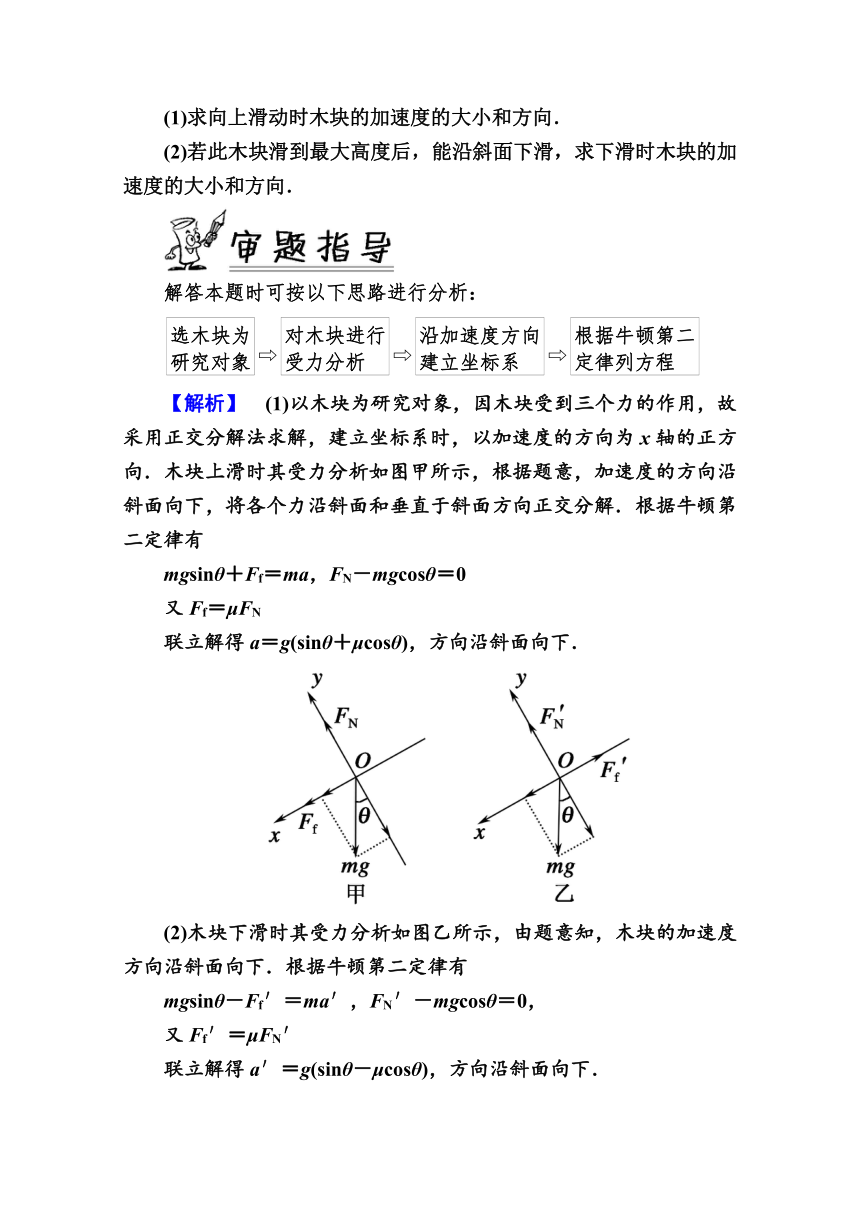
【例2】 质量为m的木块,以一定的初速度沿倾角为θ的斜面向上滑动,斜面静止不动,木块与斜面间的动摩擦因数为μ,如图所示.
(1)求向上滑动时木块的加速度的大小和方向.
(2)若此木块滑到最大高度后,能沿斜面下滑,求下滑时木块的加速度的大小和方向.
解答本题时可按以下思路进行分析:
???
【解析】 (1)以木块为研究对象,因木块受到三个力的作用,故采用正交分解法求解,建立坐标系时,以加速度的方向为x轴的正方向.木块上滑时其受力分析如图甲所示,根据题意,加速度的方向沿斜面向下,将各个力沿斜面和垂直于斜面方向正交分解.根据牛顿第二定律有
mgsinθ+Ff=ma,FN-mgcosθ=0
又Ff=μFN
联立解得a=g(sinθ+μcosθ),方向沿斜面向下.
(2)木块下滑时其受力分析如图乙所示,由题意知,木块的加速度方向沿斜面向下.根据牛顿第二定律有
mgsinθ-Ff′=ma′,FN′-mgcosθ=0,
又Ff′=μFN′
联立解得a′=g(sinθ-μcosθ),方向沿斜面向下.
【答案】 (1)g(sinθ+μcosθ),方向沿斜面向下
(2)g(sinθ-μcosθ),方向沿斜面向下
总结提能 1.当物体只受两个力的作用产生加速度时,一般采用平行四边形定则求合力,合力方向就是加速度的方向.
2.当物体受到两个以上的力作用产生加速度时,一般采用正交分解法求解,建立坐标系的原则是让尽可能多的矢量落在坐标轴上.因此,根据具体情况可以分解力,也可以分解加速度.在分解力时,往往使加速度在某一坐标轴上,另一坐标轴上的合力为零.
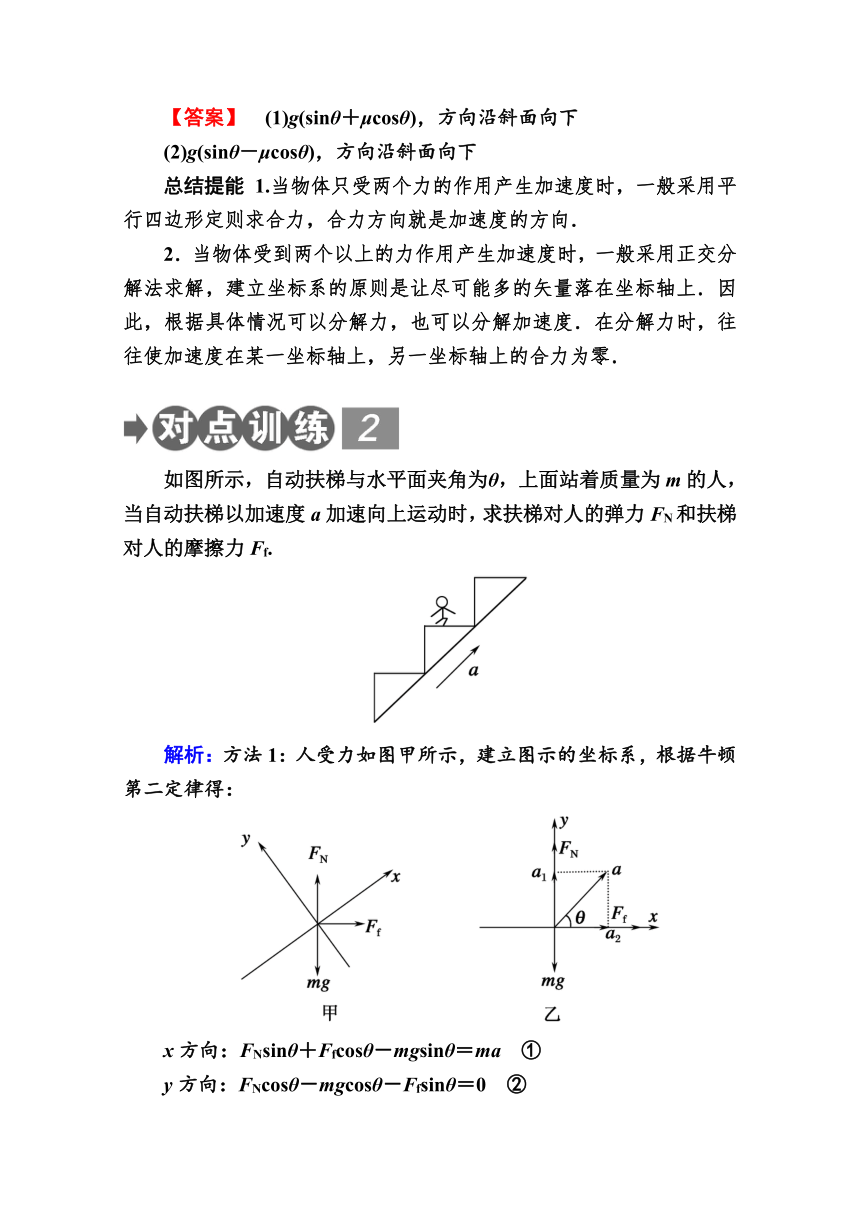
如图所示,自动扶梯与水平面夹角为θ,上面站着质量为m的人,当自动扶梯以加速度a加速向上运动时,求扶梯对人的弹力FN和扶梯对人的摩擦力Ff.
解析:方法1:人受力如图甲所示,建立图示的坐标系,根据牛顿第二定律得:
x方向:FNsinθ+Ffcosθ-mgsinθ=ma ①
y方向:FNcosθ-mgcosθ-Ffsinθ=0 ②
由①②得:FN=mg+masinθ,Ff=macosθ
方法2:如图乙建立直角坐标系,由于人的加速度方向是沿扶梯向上的,这样建立直角坐标系后,在x轴方向和y轴方向上各有一个加速度的分量,其中x轴方向的加速度分量a2=acosθ,y轴方向的加速度分量a1=asinθ.
根据牛顿第二定律知:x轴方向:Ff=ma2=macosθ,
y轴方向:FN-mg=ma1=masinθ,FN=mg+masinθ.
答案:FN=mg+masinθ,Ff=macosθ
考点三 求瞬时加速度
在应用牛顿第二定律求解物体的瞬时加速度时,经常会遇到轻绳、轻杆、轻弹簧和橡皮绳这些常见的力学模型.全面准确地理解它们的特点,可帮助我们灵活正确地分析问题.
这些模型的共同点是:都是质量可忽略的理想化模型,都会发生形变而产生弹力,同一时刻其内部弹力处处相等且与运动状态无关.这些模型的不同点是:
【例3】 如图所示,质量分别为mA和mB的A、B两球用轻弹簧连接,A球用细线悬挂起来,两球均处于静止状态.如果将悬挂A球的细线剪断,则剪断瞬间A、B两球的加速度各是多少?
解答本题的基本思路为:
(1)分析悬挂A球的细线剪断前A球和B球的受力情况;
(2)分析剪断细线瞬间有哪些力发生了变化;
(3)分析剪断细线后A球和B球的受力情况;
(4)根据牛顿第二定律列方程求解.
【解析】 由于轻弹簧两端连着小球,小球若要发生一段位移,需要一定时间,故剪断细线瞬间,弹簧的弹力与剪断前相同.
先分析剪断细线前A球和B球的受力情况,如图所示,A球受到重力mAg、弹簧的弹力F1和细线的拉力F2作用,B球受到重力mBg、弹簧的弹力F1′作用,且F1′=F1=mBg.
剪断细线瞬间,F2消失,但弹簧尚未收缩,仍保持原来的形变,即F1、F1′不变,故B球所受的力不变,所以此时aB=0,而A球的加速度为aA==,方向竖直向下.
【答案】 aA=,方向竖直向下 aB=0
总结提能 牛顿第二定律是力的瞬时作用规律,加速度和力同时产生、同时变化、同时消失.分析物体在某一时刻的瞬时加速度,关键是分析该时刻前后物体的受力情况及其变化.
注意以下两种基本模型.
(1)刚性绳模型(细钢丝、细线等):这类形变的发生和变化过程时间极短,在物体的受力情况改变(如某个力消失)的瞬间,其形变可随之突变.
(2)轻弹簧模型(轻弹簧、橡皮绳、弹性绳等):此类形变发生改变需要的时间较长,在瞬时问题中,其弹力的大小可看成是不变的.
如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g,则有( C )
A.a1=0,a2=g
B.a1=g,a2=g
C.a1=0,a2=g
D.a1=g,a2=g
解析:本题考查牛顿定律的瞬时性和连接体问题,突破点是弄清楚在抽出木板的瞬间弹簧的形变量未变,弹力不变.抽出木板的瞬间,弹力未变,故木块1所受合力仍为零,其加速度为a1=0.对于木块2受弹簧的弹力F1=mg和重力Mg,根据牛顿第二定律得:a2==g.因此C项正确.
1.(多选)在牛顿第二定律的数学表达式F=kma中,有关比例系数k的说法,正确的是( BC )
A.k的数值由F、m、a的数值决定
B.k的数值由F、m、a的单位决定
C.在国际单位制中,k=1
D.在任何情况下k都等于1
解析:物理公式在确定物理量数量关系的同时,也确定了物理量的单位.在F=kma中,只有“m”的单位取kg,“a”的单位取m/s2,“F”的单位取N时,才有k=1,故排除A、D,选项B、C正确.
2.静止在光滑水平面上的物体,受到一个水平拉力,在力刚开始作用的瞬间,下列说法中正确的是( B )
A.物体立即获得加速度和速度
B.物体立即获得加速度,但速度仍为零
C.物体立即获得速度,但加速度仍为零
D.物体的速度和加速度均为零
解析:由牛顿第二定律的同时性可知,力作用的瞬时即可获得加速度,但速度仍为零.
3.如图所示,图乙中用力F取代图甲中的m,且F=mg,其余器材完全相同,不计摩擦,图甲中小车的加速度为a1,图乙中小车的加速度为a2,则( C )
A.a1=a2 B.a1>a2
C.a1解析:本题易错之处是误认为题图甲、乙的加速度相等.题图甲中,将两者看做一个整体,对整体可得mg=(M+m)a1,解得a1=,题图乙中只有一个受力物体,故根据牛顿第二定律可得F=mg=Ma2,解得a2=,故有a14.如图所示,质量为4 kg的物体静止于光滑的水平面上,若物体受到大小为20 N,与水平方向成30°角斜向上的拉力F作用时沿水平面做匀加速运动,求物体的加速度的大小和方向.(g取10 m/s2)
解析:对物体进行受力分析,如图所示.
观察力的特点,要求合力,可将力F正交分解,则
在水平方向上有:Fx=Fcosθ;
在竖直方向上有:Fy=FN+Fsinθ-G;
由牛顿第二定律得Fx=max=ma,Fy=may=0,
所以Fcosθ=ma,
以上各式代入数据可解得
物体的加速度a≈4.33 m/s2,方向水平向右.
答案:4.33 m/s2,方向水平向右
5.目前我国高铁常使用自动闭塞法行车,自动闭塞法是通过信号机将行车区间划分为若干个闭塞分区,每个闭塞分区的首端设有信号灯,如图所示,列车向右行驶,当前一闭塞分区有列车B停车时信号灯显示红色(表示此闭塞分区有车辆停车),后一个闭塞分区显示黄色(表示要求车辆制动减速),其他闭塞分区显示绿色(表示车辆可以正常运行).假设列车A制动时所受总阻力为重力的,不考虑反应时间.(g取10 m/s2)求:
(1)如果信号系统发生故障,列车A的运行速度是30 m/s,司机看到停在路轨上的列车B才开始刹车,要使列车不发生追尾,则列车A的司机可视距离不得少于多少?
(2)如果信号系统正常,司机可视距离取问题(1)中的可视距离,列车设计运行速度为252 km/h,当司机看到黄灯开始制动,到红灯处停车,则每个闭塞分区至少需多长?
解析:(1)列车A制动时所受总阻力为重力的,由牛顿第二定律得:0.1mg=ma
加速度大小为:a=1 m/s2.
如果信号系统故障,要使列车不发生追尾,则列车制动距离不得大于可视距离,由运动学公式得:x==450 m,即列车A的司机可视距离不得少于450 m.
(2)当运行速度为v′=252 km/h=70 m/s时,
制动距离为:x′==2 450 m,
信号正常,当司机看到黄灯开始制动,到红灯处停车.每个闭塞分区的最小长度为:x′-x=2 450 m-450 m=2 000 m.
答案:(1)450 m (2)2 000 m
【例1】 (多选)下列对牛顿第二定律的表达式F=ma及其变形公式的理解,正确的是( )
A.由F=ma可知,物体所受的合力与物体的质量成正比,与物体的加速度成反比
B.由m=可知,物体的质量与其所受的合力成正比,与其运动的加速度成反比
C.由a=可知,物体的加速度与其所受的合力成正比,与其质量成反比
D.由m=可知,物体的质量可以通过测量它的加速度和它所受的合力而求出
解答本题时应把握以下两点:
(1)物体的加速度决定于物体所受的合力和物体的质量.
(2)物体的质量决定于物体本身.
【解析】 牛顿第二定律的表达式F=ma表明了各物理量之间的数量关系,即已知两个量,可以求第三个量;物体的质量由物体本身决定,与受力无关;物体所受的合力,是由和它相互作用的物体共同产生的,与物体的质量和加速度无关;而由a=可知,物体的加速度与所受合外力成正比,与其质量成反比.综上分析知,选项A、B错误,C、D正确.
【答案】 CD
总结提能 a=是加速度的决定式,故a与F成正比,与m成反比,由其变形公式m=可以求解物体的质量,但不能认为m与F成正比,与a成反比.
一物体在多个力的作用下处于静止状态,如果仅使其中某个力的大小逐渐减小到零,然后又逐渐从零恢复到原来大小,在上述过程中,此力的方向一直保持不变,那么如图所示的v-t图象中,可能符合此过程中物体运动情况的是( D )
解析:其中的一个力逐渐减小到零的过程中,物体受到的合力逐渐增大,则其加速度逐渐增大,速度时间图象中图线的斜率表示加速度,所以在力逐渐减小到零的过程中,图线的斜率的绝对值逐渐增大,当这个力又从零恢复到原来大小时,合力逐渐减小,加速度逐渐减小,图线斜率的绝对值逐渐减小,只有D符合题意.
考点二 正交分解法在牛顿第二定律解题中的应用
正交分解法是把一个矢量分解在两个互相垂直的坐标轴上的方法,是一种常用的矢量运算方法.其实质是将复杂的矢量运算转化为简单的代数运算,从而简捷方便地解题,是解牛顿第二定律问题的基本方法.物体在受到三个或三个以上的力的作用时,一般都用正交分解法.
表示方法
为减少矢量的分解,在建立正交坐标系时,应使尽可能多的矢量落在两个坐标轴上,因此,确定x轴正方向有两种方法.
(1)分解力而不分解加速度:通常以加速度的方向为x轴的正方向,建立正交坐标系,将物体所受的各个力分解到x轴和y轴上,分别得x轴和y轴上的合力Fx和Fy,根据力的独立作用原理列方程组
(2)分解加速度而不分解力:若物体受几个相互垂直的力的作用,应用牛顿定律求解时,如果仍分解力就比较烦琐,所以在建立正交坐标系时,可根据物体的受力情况,以某个力的方向为x轴的正方向,使尽可能多的力落在坐标轴上而分解加速度a,得ax和ay,根据牛顿第二定律列方程组
温馨提示:正交分解建立坐标系的原则:
(1)一般情况:以加速度的方向为一个坐标轴的正方向,垂直于加速度的方向为另一坐标轴的方向.
(2)特殊情况:所有力都在两个互相垂直的方向上,而加速度不在这两个方向上,建立坐标系时应使各个力都在坐标轴上,即分解加速度而不分解力.
【例2】 质量为m的木块,以一定的初速度沿倾角为θ的斜面向上滑动,斜面静止不动,木块与斜面间的动摩擦因数为μ,如图所示.
(1)求向上滑动时木块的加速度的大小和方向.
(2)若此木块滑到最大高度后,能沿斜面下滑,求下滑时木块的加速度的大小和方向.
解答本题时可按以下思路进行分析:
???
【解析】 (1)以木块为研究对象,因木块受到三个力的作用,故采用正交分解法求解,建立坐标系时,以加速度的方向为x轴的正方向.木块上滑时其受力分析如图甲所示,根据题意,加速度的方向沿斜面向下,将各个力沿斜面和垂直于斜面方向正交分解.根据牛顿第二定律有
mgsinθ+Ff=ma,FN-mgcosθ=0
又Ff=μFN
联立解得a=g(sinθ+μcosθ),方向沿斜面向下.
(2)木块下滑时其受力分析如图乙所示,由题意知,木块的加速度方向沿斜面向下.根据牛顿第二定律有
mgsinθ-Ff′=ma′,FN′-mgcosθ=0,
又Ff′=μFN′
联立解得a′=g(sinθ-μcosθ),方向沿斜面向下.
【答案】 (1)g(sinθ+μcosθ),方向沿斜面向下
(2)g(sinθ-μcosθ),方向沿斜面向下
总结提能 1.当物体只受两个力的作用产生加速度时,一般采用平行四边形定则求合力,合力方向就是加速度的方向.
2.当物体受到两个以上的力作用产生加速度时,一般采用正交分解法求解,建立坐标系的原则是让尽可能多的矢量落在坐标轴上.因此,根据具体情况可以分解力,也可以分解加速度.在分解力时,往往使加速度在某一坐标轴上,另一坐标轴上的合力为零.
如图所示,自动扶梯与水平面夹角为θ,上面站着质量为m的人,当自动扶梯以加速度a加速向上运动时,求扶梯对人的弹力FN和扶梯对人的摩擦力Ff.
解析:方法1:人受力如图甲所示,建立图示的坐标系,根据牛顿第二定律得:
x方向:FNsinθ+Ffcosθ-mgsinθ=ma ①
y方向:FNcosθ-mgcosθ-Ffsinθ=0 ②
由①②得:FN=mg+masinθ,Ff=macosθ
方法2:如图乙建立直角坐标系,由于人的加速度方向是沿扶梯向上的,这样建立直角坐标系后,在x轴方向和y轴方向上各有一个加速度的分量,其中x轴方向的加速度分量a2=acosθ,y轴方向的加速度分量a1=asinθ.
根据牛顿第二定律知:x轴方向:Ff=ma2=macosθ,
y轴方向:FN-mg=ma1=masinθ,FN=mg+masinθ.
答案:FN=mg+masinθ,Ff=macosθ
考点三 求瞬时加速度
在应用牛顿第二定律求解物体的瞬时加速度时,经常会遇到轻绳、轻杆、轻弹簧和橡皮绳这些常见的力学模型.全面准确地理解它们的特点,可帮助我们灵活正确地分析问题.
这些模型的共同点是:都是质量可忽略的理想化模型,都会发生形变而产生弹力,同一时刻其内部弹力处处相等且与运动状态无关.这些模型的不同点是:
【例3】 如图所示,质量分别为mA和mB的A、B两球用轻弹簧连接,A球用细线悬挂起来,两球均处于静止状态.如果将悬挂A球的细线剪断,则剪断瞬间A、B两球的加速度各是多少?
解答本题的基本思路为:
(1)分析悬挂A球的细线剪断前A球和B球的受力情况;
(2)分析剪断细线瞬间有哪些力发生了变化;
(3)分析剪断细线后A球和B球的受力情况;
(4)根据牛顿第二定律列方程求解.
【解析】 由于轻弹簧两端连着小球,小球若要发生一段位移,需要一定时间,故剪断细线瞬间,弹簧的弹力与剪断前相同.
先分析剪断细线前A球和B球的受力情况,如图所示,A球受到重力mAg、弹簧的弹力F1和细线的拉力F2作用,B球受到重力mBg、弹簧的弹力F1′作用,且F1′=F1=mBg.
剪断细线瞬间,F2消失,但弹簧尚未收缩,仍保持原来的形变,即F1、F1′不变,故B球所受的力不变,所以此时aB=0,而A球的加速度为aA==,方向竖直向下.
【答案】 aA=,方向竖直向下 aB=0
总结提能 牛顿第二定律是力的瞬时作用规律,加速度和力同时产生、同时变化、同时消失.分析物体在某一时刻的瞬时加速度,关键是分析该时刻前后物体的受力情况及其变化.
注意以下两种基本模型.
(1)刚性绳模型(细钢丝、细线等):这类形变的发生和变化过程时间极短,在物体的受力情况改变(如某个力消失)的瞬间,其形变可随之突变.
(2)轻弹簧模型(轻弹簧、橡皮绳、弹性绳等):此类形变发生改变需要的时间较长,在瞬时问题中,其弹力的大小可看成是不变的.
如图所示,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2.重力加速度大小为g,则有( C )
A.a1=0,a2=g
B.a1=g,a2=g
C.a1=0,a2=g
D.a1=g,a2=g
解析:本题考查牛顿定律的瞬时性和连接体问题,突破点是弄清楚在抽出木板的瞬间弹簧的形变量未变,弹力不变.抽出木板的瞬间,弹力未变,故木块1所受合力仍为零,其加速度为a1=0.对于木块2受弹簧的弹力F1=mg和重力Mg,根据牛顿第二定律得:a2==g.因此C项正确.
1.(多选)在牛顿第二定律的数学表达式F=kma中,有关比例系数k的说法,正确的是( BC )
A.k的数值由F、m、a的数值决定
B.k的数值由F、m、a的单位决定
C.在国际单位制中,k=1
D.在任何情况下k都等于1
解析:物理公式在确定物理量数量关系的同时,也确定了物理量的单位.在F=kma中,只有“m”的单位取kg,“a”的单位取m/s2,“F”的单位取N时,才有k=1,故排除A、D,选项B、C正确.
2.静止在光滑水平面上的物体,受到一个水平拉力,在力刚开始作用的瞬间,下列说法中正确的是( B )
A.物体立即获得加速度和速度
B.物体立即获得加速度,但速度仍为零
C.物体立即获得速度,但加速度仍为零
D.物体的速度和加速度均为零
解析:由牛顿第二定律的同时性可知,力作用的瞬时即可获得加速度,但速度仍为零.
3.如图所示,图乙中用力F取代图甲中的m,且F=mg,其余器材完全相同,不计摩擦,图甲中小车的加速度为a1,图乙中小车的加速度为a2,则( C )
A.a1=a2 B.a1>a2
C.a1
解析:对物体进行受力分析,如图所示.
观察力的特点,要求合力,可将力F正交分解,则
在水平方向上有:Fx=Fcosθ;
在竖直方向上有:Fy=FN+Fsinθ-G;
由牛顿第二定律得Fx=max=ma,Fy=may=0,
所以Fcosθ=ma,
以上各式代入数据可解得
物体的加速度a≈4.33 m/s2,方向水平向右.
答案:4.33 m/s2,方向水平向右
5.目前我国高铁常使用自动闭塞法行车,自动闭塞法是通过信号机将行车区间划分为若干个闭塞分区,每个闭塞分区的首端设有信号灯,如图所示,列车向右行驶,当前一闭塞分区有列车B停车时信号灯显示红色(表示此闭塞分区有车辆停车),后一个闭塞分区显示黄色(表示要求车辆制动减速),其他闭塞分区显示绿色(表示车辆可以正常运行).假设列车A制动时所受总阻力为重力的,不考虑反应时间.(g取10 m/s2)求:
(1)如果信号系统发生故障,列车A的运行速度是30 m/s,司机看到停在路轨上的列车B才开始刹车,要使列车不发生追尾,则列车A的司机可视距离不得少于多少?
(2)如果信号系统正常,司机可视距离取问题(1)中的可视距离,列车设计运行速度为252 km/h,当司机看到黄灯开始制动,到红灯处停车,则每个闭塞分区至少需多长?
解析:(1)列车A制动时所受总阻力为重力的,由牛顿第二定律得:0.1mg=ma
加速度大小为:a=1 m/s2.
如果信号系统故障,要使列车不发生追尾,则列车制动距离不得大于可视距离,由运动学公式得:x==450 m,即列车A的司机可视距离不得少于450 m.
(2)当运行速度为v′=252 km/h=70 m/s时,
制动距离为:x′==2 450 m,
信号正常,当司机看到黄灯开始制动,到红灯处停车.每个闭塞分区的最小长度为:x′-x=2 450 m-450 m=2 000 m.
答案:(1)450 m (2)2 000 m
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
