高一物理人教版必修1学案 3.2 弹力 Word版含解析
文档属性
| 名称 | 高一物理人教版必修1学案 3.2 弹力 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-03 13:05:43 | ||
图片预览



文档简介
2 弹力
【例1】 分别画出图中的物体A所受弹力的示意图.
本题中,画示意图的基本步骤为:
【解析】 分析此类问题的关键是确定接触面,对于点—面接触、面—面接触类问题,其中的面即为接触面;对于点—弧面接触类问题,过接触点的弧面的切面即为接触面.根据弹力垂直于接触面,可判断物体A所受的弹力方向,作出的示意图如图所示.
【答案】 见解析
总结提能 弹力的方向可根据弹力作用的类型进行判断.
1.面面接触:弹力垂直于接触面(或切面)指向受力物体.
2.点面接触:弹力过点垂直于接触面(或切面)指向受力物体.
3.轻绳:绳对物体的拉力沿绳并指向绳收缩的方向.
4.轻弹簧:弹簧对物体的弹力可能为支持力,也可能为拉力,但一定沿弹簧的轴线方向.
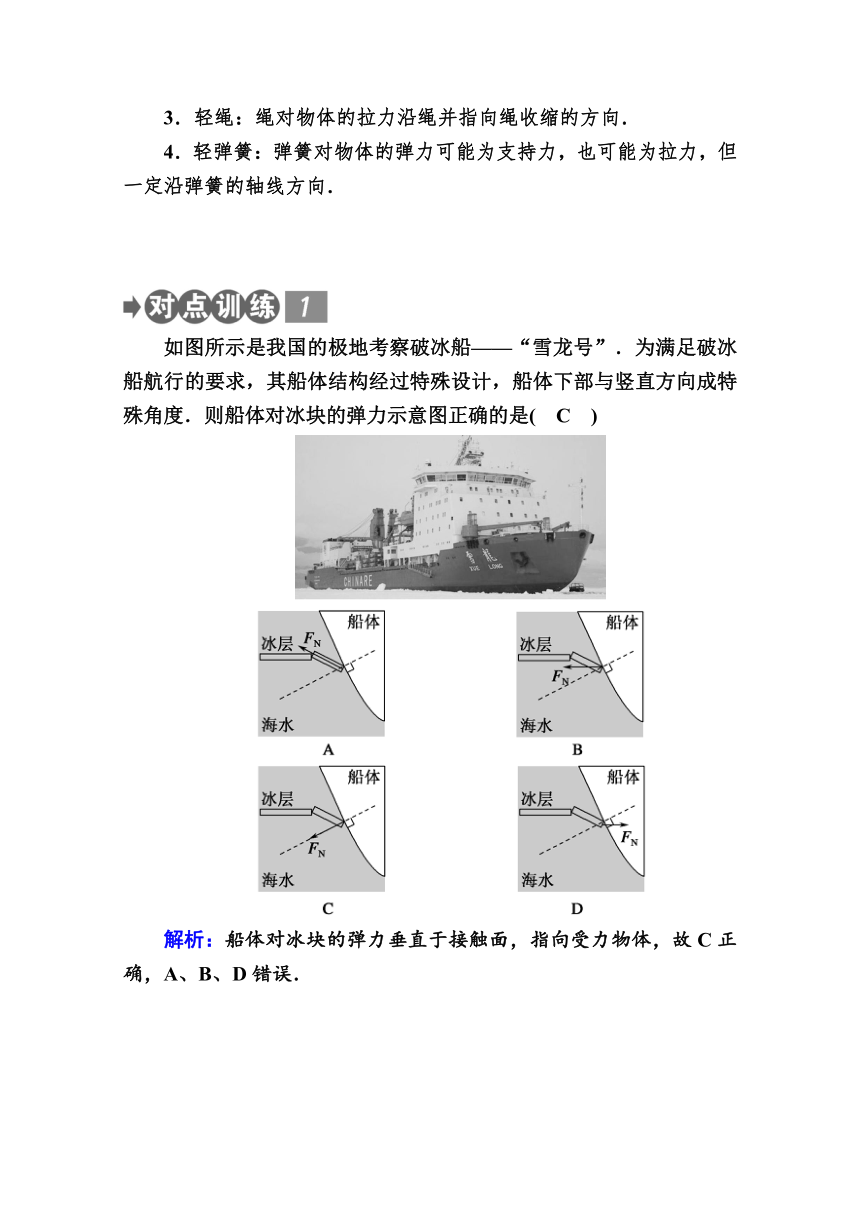
如图所示是我国的极地考察破冰船——“雪龙号”.为满足破冰船航行的要求,其船体结构经过特殊设计,船体下部与竖直方向成特殊角度.则船体对冰块的弹力示意图正确的是( C )
解析:船体对冰块的弹力垂直于接触面,指向受力物体,故C正确,A、B、D错误.
考点二 物体间弹力有无的判断方法
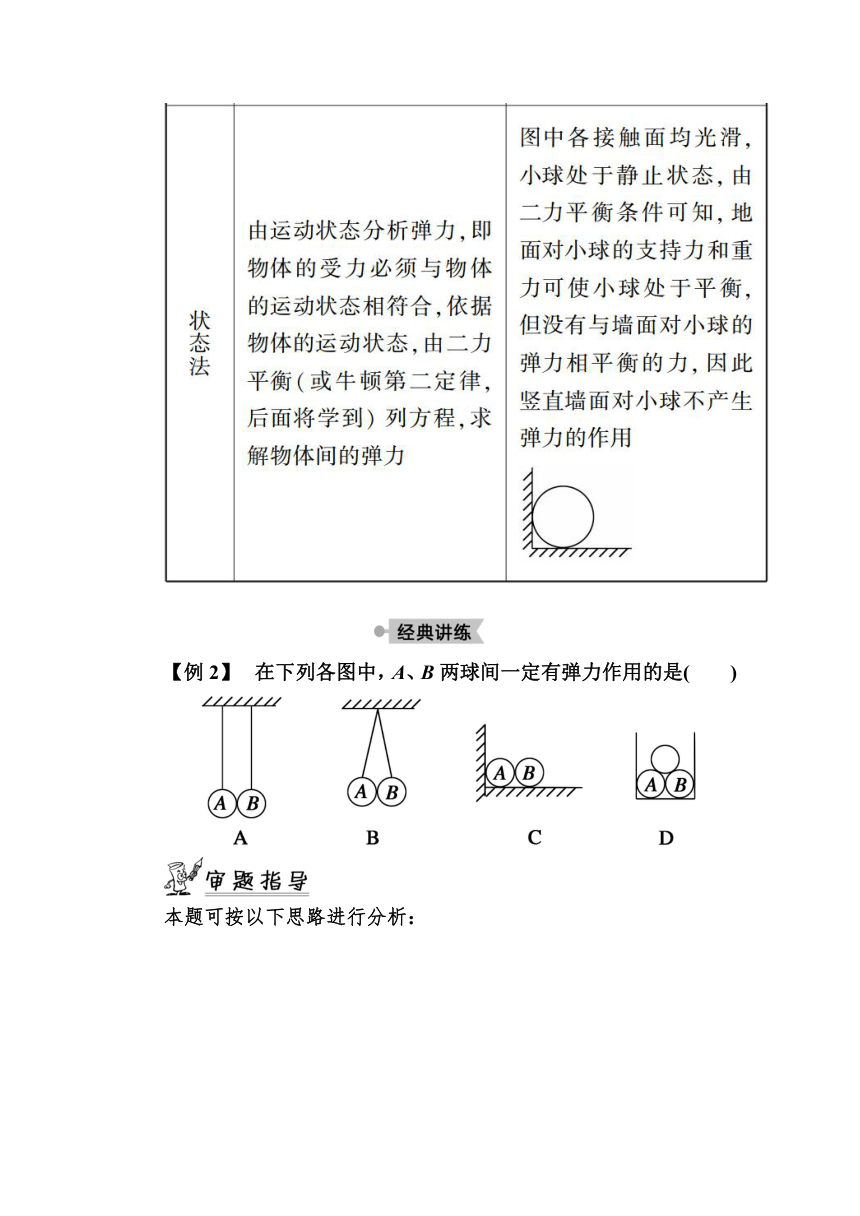
【例2】 在下列各图中,A、B两球间一定有弹力作用的是( )
本题可按以下思路进行分析:
【解析】 在A图中,若拿去A球,则B球静止不动,故A、B间没有挤压,即A、B间没有弹力.在B图中,若拿去A球,则B球将向左运动,故A、B间存在相互挤压,即A、B间存在弹力.在C图中,若拿去A球,则B球静止不动,故A、B间没有挤压,即A、B间没有弹力.在D图中,不能判断A、B间有没有弹力.故选项B正确.
【答案】 B
总结提能 弹力的产生条件中接触是前提,挤压是关键,相互接触的物体是否发生弹性形变是弹力存在与否的标志.但是,实际上除弹簧、橡皮条等物体产生弹力时形变较明显外,大部分物体产生弹力时形变是微小的,肉眼很难观察出来.因此,弹力有无的判断主要有以下两种方法:(1)条件法,(2)假设法.
如图所示,将一个钢球分别放在烧杯、口大底小的普通茶杯和三角烧杯中,钢球在各容器的底部与侧壁相接触,处于静止状态.若钢球和各容器都是光滑的,各容器的底部均处于水平面内,则以下说法中正确的是( A )
A.各容器的侧壁对钢球均无弹力作用
B.各容器的侧壁对钢球均有弹力作用
C.烧杯的侧壁对钢球无弹力作用,其余两种容器的侧壁对钢球均有弹力作用
D.口大底小的普通茶杯的侧壁对钢球有弹力作用,其余两种容器的侧壁对钢球均无弹力作用
解析:钢球与容器的侧壁接触,是否有弹力作用,就看接触处是否发生弹性形变,但微小形变难以觉察,可借助假设法判断.
假设容器侧壁对钢球无弹力作用,则钢球受重力和容器底部对它的支持力作用,钢球仍将处于静止状态,故钢球与容器侧壁虽然接触但没有发生弹性形变,即容器侧壁对钢球无弹力作用的假设成立.
也可以假设容器侧壁对钢球有弹力作用,作出各容器中钢球的受力示意图如图所示,可见三种情况均与钢球静止的题设条件相矛盾,所以该假设不成立,各容器的侧壁对钢球均无弹力作用.
考点三 弹力大小的计算
1.胡克定律及其应用
胡克定律表明,弹力的大小与弹簧的形变量成正比,而不是与弹簧的长度成正比.即胡克定律表达式F=kx中的x是弹簧的形变量,而不是弹簧的原长或变化后的长度.
应用胡克定律时应注意下列问题:
(1)弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,不是弹簧的原长,也不是弹簧形变后的实际长度.
(3)F-x图象为一条经过原点的倾斜直线,图象斜率表示弹簧的劲度系数,对于同一根弹簧来说,劲度系数是不变的.
(4)由于F1=kx1,F2=kx2,故ΔF=F2-F1=kx2-kx1=kΔx,因此,弹簧上弹力的变化量ΔF与形变量的变化量也成正比关系.
2.一般弹力的计算
对于除弹簧外的其他弹性体的弹力大小的计算,一般要借助物体的运动状态所遵循的物理规律求解.比如悬挂在竖直细绳上的物体处于静止状态时,物体受绳向上的拉力和竖直向下的重力作用,根据二力平衡,可知绳的拉力大小等于物体重力的大小.
关键:弹簧弹力用胡克定律,一般弹力用二力平衡.
特别提醒:胡克定律只能计算弹簧的弹力大小,而弹簧的弹力方向,要根据是被拉伸,还是被压缩来确定,其方向总是与弹簧恢复原状的方向相同.
【例3】 (多选)如图所示,A、B两物体的重力分别是GA=3 N,GB=4 N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧的弹力F=2 N,则细线中的张力FT及B对地面的压力FN的可能值分别是( )
A.5 N和6 N B.5 N和2 N
C.1 N和6 N D.1 N和2 N
本题的解题思路为:
【解析】 如果弹簧处于被拉伸的状态,它将有收缩到原状的趋势,会向下拉A,向上提B,则对物体A、B,有FT=GA+F=5 N,FN=GB-F=2 N,选项B正确;如果弹簧处于被压缩的状态,它将有向两端伸长恢复原状的趋势,会向上推A,向下压B,则FT′=GA-F=1 N,FN′=GB+F=6 N,选项C正确.
【答案】 BC
总结提能 应用胡克定律F=kx解题时,必须注意:
(1)弹簧的形变必须在弹性限度内;
(2)x是弹簧的形变量,不是弹簧形变后的实际长度.
如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时球在A处,今用力F压球使弹簧缩短x球至B处,则此时弹簧的弹力为( B )
A.kx B.kx+G
C.G-kx D.以上都不对
解析:设球在A处时弹簧已压缩了Δx,球平衡时弹力FA=G=kΔx,球在B处时,弹簧又压缩x,球再达到平衡时弹力FB=k(Δx+x)=G+kx.故选项B是正确的.
考点四 探究弹力和弹簧伸长的关系
1.实验目的
(1)探究弹力与弹簧的伸长量的定量关系.
(2)学会利用图象研究两个物理量之间的关系的方法.
2.实验原理
(1)如图所示,在弹簧下端悬挂钩码时弹簧会伸长,平衡时弹簧产生的弹力与钩码的重力大小相等.
(2)用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x,F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系.
3.实验器材
轻质弹簧(一根),钩码(一盒),刻度尺,铁架台,重垂线,坐标纸,三角板.
4.实验步骤
(1)将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧自然伸长状态时的长度l0,即原长.
(2)如图所示,将已知质量的钩码挂在弹簧的下端,在平衡时测出弹簧的总长并计算钩码的重力,填写在记录表格里.
(3)改变所挂钩码的质量,重复上步的实验过程多次.
5.数据处理
(1)以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线,如图所示.
(2)以弹簧伸长量为自变量,写出弹力和弹簧伸长量之间的函数表达式,函数表达式中常数即为弹簧的劲度系数,这个常数也可据F-x图线的斜率求解,k=.
6.注意事项
(1)所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度.
(2)每次所挂钩码的质量差尽量大一些,从而使在坐标系上描的点尽可能稀疏一些,这样作出的图线更精确.
(3)测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量,刻度尺要保持竖直并靠近弹簧,以免增大误差.
(4)记录数据时要注意弹力及弹簧伸长量的对应关系及单位.
(5)描点画线时,所描的点不一定都落在一条图线上,但应注意一定要使各点均匀分布在图线的两侧.
7.误差分析
(1)由于弹簧原长及伸长量的测量都不便于操作,故存在较大的测量误差.
(2)由于弹簧自身的重力的影响也会造成误差.
当未挂重物时,弹簧在自身重力的作用下,已经有一个伸长量,这样在作图线时,图线与x轴有一截距.
【例4】 某同学在做“探究弹力和弹簧伸长量的关系”的实验中,所用实验装置如图所示,所用的钩码每只质量都是30 g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在下表中.实验中弹簧始终未超过弹性限度,取g=10 m/s2.试根据这些实验数据在如图所示的坐标系中作出弹簧弹力大小与弹簧总长度之间的函数关系的图线.
钩码质量(g) 0 30 60 90 120 150
弹簧总长度(cm) 6.00 7.00 8.00 9.00 10.00 11.00
(1)该图线的函数表达式为F=________N;
(2)该弹簧的劲度系数k=________N/m;
(3)图线与横轴的交点的物理意义是________;
(4)图线延长后与纵轴的交点的物理意义是________.
在坐标系中描点作图,通过图象研究规律,再结合物理规律,明确图象的斜率、截距的物理意义.解题思路如下:
【解析】 描点作图,图象如图所示.
(1)由图象可以得出图线的函数表达式为F=(30L-1.8) N;
(2)图线的斜率即为弹簧的劲度系数k=30 N/m;
(3)图线与横轴的交点表示弹簧弹力F=0时弹簧的长度,即弹簧的原长;
(4)图线延长后与纵轴的交点表示弹簧长度为5 cm时的弹力,此时弹簧被压缩了1 cm,即表示弹簧被压缩1 cm时的弹力.
【答案】 图线见解析 (1)(30L-1.8) (2)30 (3)见解析 (4)见解析
总结提能 图象法是处理实验数据的一种常用方法,在物理学中经常用图象处理物理问题,解答这类问题时必须明确:(1)图线斜率的物理意义(或切线斜率的物理意义);(2)图线与纵轴、横轴交点的物理意义.
以下是一位同学做“探究弹簧弹力与弹簧伸长量的关系”的实验.
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来:CBDAEF.
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数
据(x,F)对应的点,并用平滑的曲线连接起来
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式
F.解释函数表达式中常数的物理意义
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
弹簧的弹力(F/N) 0.5 1.0 1.5 2.0 2.5
弹簧的原长度(L0/cm) 15 15 15 15 15
弹簧的长度(L/cm) 16.2 17.3 18.5 19.6 20.8
弹簧的伸长量(x/cm)
①写出曲线的函数表达式(x用cm作单位):F=0.43x.
②函数表达式中常数的物理意义:弹簧的劲度系数.
解析:(1)按实验操作的先后顺序,步骤为:CBDAEF.
(2)①k==0.43 N/cm,得F=0.43x.
②常数为弹簧的劲度系数.
1.(多选)下列各种情况中,属于弹性形变的有( AB )
A.撑竿跳高运动员起跳中,撑竿的形变
B.当你坐在椅子上时,椅面发生的微小形变
C.细钢丝被绕制成弹簧
D.铝桶被砸扁
解析:本题考查对弹性形变的理解.“撑竿的形变”“椅面发生的微小形变”均能恢复原状,是弹性形变;“细钢丝被绕制成弹簧”不能恢复成“钢丝”,“铝桶被砸扁”不能恢复成“桶”,是非弹性形变,故选项A、B正确,C、D错误.
2.体育课上一学生将足球踢向斜台,如图所示.下列关于斜台对足球的弹力的方向,说法正确的是( D )
A.沿v1的方向
B.先沿v1的方向后沿v2的方向
C.沿v2的方向
D.沿垂直于斜台斜向左上方的方向
解析:支持力是弹力,方向总是垂直于接触面,并指向被支持物,所以斜台对足球的弹力方向为垂直于斜台斜向左上方,故D正确.
3.一辆汽车停在水平地面上,下列说法中正确的是( C )
A.地面受到了向下的弹力,是因为地面发生了弹性形变;汽车没有发生形变,所以汽车不受弹力
B.地面受到了向下的弹力,是因为地面发生了弹性形变;汽车受到了向上的弹力,是因为汽车也发生了形变
C.汽车受到向上的弹力,是因为地面发生了形变;地面受到向下的弹力,是因为汽车发生了形变
D.以上说法都不正确
解析:汽车停在水平地面上,汽车受到的弹力是因为地面发生了形变而又要恢复原状从而对阻碍其恢复的物体产生的作用力;地面受到的弹力是由于汽车发生了形变又要恢复原状从而对阻碍其恢复的地面产生的作用力,故选项C正确,A、B、D错误.
4.在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如下图(1)所示连接起来进行探究.
钩码数 1 2 3 4
LA/cm 15.71 19.71 23.66 27.76
LB/cm 29.96 35.76 41.51 47.36
(1)某次测量如下图(2)所示,指针示数为16.00 cm.
(2)在弹性限度内,将50 g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如上表.用表中数据计算弹簧Ⅰ的劲度系数为12.45 N/m(重力加速度g=10 m/s2),由表中数据能(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数.
解析:(1)指针示数为160.0 mm=16.00 cm.(2)由3mg=k1(LA4-LA1)解得k1== N/m≈12.45 N/m.同理也能计算出弹簧Ⅱ的劲度系数.
5.请在下图中画出杆或球所受的弹力.
(a)杆靠在墙上;
(b)杆放在半球形的槽中;
(c)球用细线悬挂在竖直墙上;
(d)点1、2、3都可能是球的重心位置,点2是球心,点1、2、3在同一竖直线上.
解析:本题考查对弹力方向的判定,关键是熟悉各种接触中的弹力方向.
(a)杆在重力作用下对A、B两处都产生挤压作用,故A、B两处对杆都有弹力,弹力方向与接触点的平面垂直.如图(a)所示.
(b)杆对C、D两处都有挤压作用,因C处为曲面,D处为支撑点,所以C处弹力垂直于其切面指向球心,D处弹力垂直于杆斜向上.如图(b)所示.
(c)球挤压墙壁且拉紧绳子,所以墙对球的弹力与墙面垂直;绳子对球的弹力沿绳子斜向上.如图(c)所示.
(d)当重心不在球心处时,弹力作用也必通过球心点2,如图(d)所示.应注意不要错误地认为弹力作用线必定通过球的重心.
答案:图见解析
【例1】 分别画出图中的物体A所受弹力的示意图.
本题中,画示意图的基本步骤为:
【解析】 分析此类问题的关键是确定接触面,对于点—面接触、面—面接触类问题,其中的面即为接触面;对于点—弧面接触类问题,过接触点的弧面的切面即为接触面.根据弹力垂直于接触面,可判断物体A所受的弹力方向,作出的示意图如图所示.
【答案】 见解析
总结提能 弹力的方向可根据弹力作用的类型进行判断.
1.面面接触:弹力垂直于接触面(或切面)指向受力物体.
2.点面接触:弹力过点垂直于接触面(或切面)指向受力物体.
3.轻绳:绳对物体的拉力沿绳并指向绳收缩的方向.
4.轻弹簧:弹簧对物体的弹力可能为支持力,也可能为拉力,但一定沿弹簧的轴线方向.
如图所示是我国的极地考察破冰船——“雪龙号”.为满足破冰船航行的要求,其船体结构经过特殊设计,船体下部与竖直方向成特殊角度.则船体对冰块的弹力示意图正确的是( C )
解析:船体对冰块的弹力垂直于接触面,指向受力物体,故C正确,A、B、D错误.
考点二 物体间弹力有无的判断方法
【例2】 在下列各图中,A、B两球间一定有弹力作用的是( )
本题可按以下思路进行分析:
【解析】 在A图中,若拿去A球,则B球静止不动,故A、B间没有挤压,即A、B间没有弹力.在B图中,若拿去A球,则B球将向左运动,故A、B间存在相互挤压,即A、B间存在弹力.在C图中,若拿去A球,则B球静止不动,故A、B间没有挤压,即A、B间没有弹力.在D图中,不能判断A、B间有没有弹力.故选项B正确.
【答案】 B
总结提能 弹力的产生条件中接触是前提,挤压是关键,相互接触的物体是否发生弹性形变是弹力存在与否的标志.但是,实际上除弹簧、橡皮条等物体产生弹力时形变较明显外,大部分物体产生弹力时形变是微小的,肉眼很难观察出来.因此,弹力有无的判断主要有以下两种方法:(1)条件法,(2)假设法.
如图所示,将一个钢球分别放在烧杯、口大底小的普通茶杯和三角烧杯中,钢球在各容器的底部与侧壁相接触,处于静止状态.若钢球和各容器都是光滑的,各容器的底部均处于水平面内,则以下说法中正确的是( A )
A.各容器的侧壁对钢球均无弹力作用
B.各容器的侧壁对钢球均有弹力作用
C.烧杯的侧壁对钢球无弹力作用,其余两种容器的侧壁对钢球均有弹力作用
D.口大底小的普通茶杯的侧壁对钢球有弹力作用,其余两种容器的侧壁对钢球均无弹力作用
解析:钢球与容器的侧壁接触,是否有弹力作用,就看接触处是否发生弹性形变,但微小形变难以觉察,可借助假设法判断.
假设容器侧壁对钢球无弹力作用,则钢球受重力和容器底部对它的支持力作用,钢球仍将处于静止状态,故钢球与容器侧壁虽然接触但没有发生弹性形变,即容器侧壁对钢球无弹力作用的假设成立.
也可以假设容器侧壁对钢球有弹力作用,作出各容器中钢球的受力示意图如图所示,可见三种情况均与钢球静止的题设条件相矛盾,所以该假设不成立,各容器的侧壁对钢球均无弹力作用.
考点三 弹力大小的计算
1.胡克定律及其应用
胡克定律表明,弹力的大小与弹簧的形变量成正比,而不是与弹簧的长度成正比.即胡克定律表达式F=kx中的x是弹簧的形变量,而不是弹簧的原长或变化后的长度.
应用胡克定律时应注意下列问题:
(1)弹簧发生形变时必须在弹性限度内.
(2)x是弹簧的形变量,不是弹簧的原长,也不是弹簧形变后的实际长度.
(3)F-x图象为一条经过原点的倾斜直线,图象斜率表示弹簧的劲度系数,对于同一根弹簧来说,劲度系数是不变的.
(4)由于F1=kx1,F2=kx2,故ΔF=F2-F1=kx2-kx1=kΔx,因此,弹簧上弹力的变化量ΔF与形变量的变化量也成正比关系.
2.一般弹力的计算
对于除弹簧外的其他弹性体的弹力大小的计算,一般要借助物体的运动状态所遵循的物理规律求解.比如悬挂在竖直细绳上的物体处于静止状态时,物体受绳向上的拉力和竖直向下的重力作用,根据二力平衡,可知绳的拉力大小等于物体重力的大小.
关键:弹簧弹力用胡克定律,一般弹力用二力平衡.
特别提醒:胡克定律只能计算弹簧的弹力大小,而弹簧的弹力方向,要根据是被拉伸,还是被压缩来确定,其方向总是与弹簧恢复原状的方向相同.
【例3】 (多选)如图所示,A、B两物体的重力分别是GA=3 N,GB=4 N.A用细线悬挂在顶板上,B放在水平面上,A、B间轻弹簧的弹力F=2 N,则细线中的张力FT及B对地面的压力FN的可能值分别是( )
A.5 N和6 N B.5 N和2 N
C.1 N和6 N D.1 N和2 N
本题的解题思路为:
【解析】 如果弹簧处于被拉伸的状态,它将有收缩到原状的趋势,会向下拉A,向上提B,则对物体A、B,有FT=GA+F=5 N,FN=GB-F=2 N,选项B正确;如果弹簧处于被压缩的状态,它将有向两端伸长恢复原状的趋势,会向上推A,向下压B,则FT′=GA-F=1 N,FN′=GB+F=6 N,选项C正确.
【答案】 BC
总结提能 应用胡克定律F=kx解题时,必须注意:
(1)弹簧的形变必须在弹性限度内;
(2)x是弹簧的形变量,不是弹簧形变后的实际长度.
如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时球在A处,今用力F压球使弹簧缩短x球至B处,则此时弹簧的弹力为( B )
A.kx B.kx+G
C.G-kx D.以上都不对
解析:设球在A处时弹簧已压缩了Δx,球平衡时弹力FA=G=kΔx,球在B处时,弹簧又压缩x,球再达到平衡时弹力FB=k(Δx+x)=G+kx.故选项B是正确的.
考点四 探究弹力和弹簧伸长的关系
1.实验目的
(1)探究弹力与弹簧的伸长量的定量关系.
(2)学会利用图象研究两个物理量之间的关系的方法.
2.实验原理
(1)如图所示,在弹簧下端悬挂钩码时弹簧会伸长,平衡时弹簧产生的弹力与钩码的重力大小相等.
(2)用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x,F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系.
3.实验器材
轻质弹簧(一根),钩码(一盒),刻度尺,铁架台,重垂线,坐标纸,三角板.
4.实验步骤
(1)将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧自然伸长状态时的长度l0,即原长.
(2)如图所示,将已知质量的钩码挂在弹簧的下端,在平衡时测出弹簧的总长并计算钩码的重力,填写在记录表格里.
(3)改变所挂钩码的质量,重复上步的实验过程多次.
5.数据处理
(1)以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线,如图所示.
(2)以弹簧伸长量为自变量,写出弹力和弹簧伸长量之间的函数表达式,函数表达式中常数即为弹簧的劲度系数,这个常数也可据F-x图线的斜率求解,k=.
6.注意事项
(1)所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度.
(2)每次所挂钩码的质量差尽量大一些,从而使在坐标系上描的点尽可能稀疏一些,这样作出的图线更精确.
(3)测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量,刻度尺要保持竖直并靠近弹簧,以免增大误差.
(4)记录数据时要注意弹力及弹簧伸长量的对应关系及单位.
(5)描点画线时,所描的点不一定都落在一条图线上,但应注意一定要使各点均匀分布在图线的两侧.
7.误差分析
(1)由于弹簧原长及伸长量的测量都不便于操作,故存在较大的测量误差.
(2)由于弹簧自身的重力的影响也会造成误差.
当未挂重物时,弹簧在自身重力的作用下,已经有一个伸长量,这样在作图线时,图线与x轴有一截距.
【例4】 某同学在做“探究弹力和弹簧伸长量的关系”的实验中,所用实验装置如图所示,所用的钩码每只质量都是30 g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,并将数据填在下表中.实验中弹簧始终未超过弹性限度,取g=10 m/s2.试根据这些实验数据在如图所示的坐标系中作出弹簧弹力大小与弹簧总长度之间的函数关系的图线.
钩码质量(g) 0 30 60 90 120 150
弹簧总长度(cm) 6.00 7.00 8.00 9.00 10.00 11.00
(1)该图线的函数表达式为F=________N;
(2)该弹簧的劲度系数k=________N/m;
(3)图线与横轴的交点的物理意义是________;
(4)图线延长后与纵轴的交点的物理意义是________.
在坐标系中描点作图,通过图象研究规律,再结合物理规律,明确图象的斜率、截距的物理意义.解题思路如下:
【解析】 描点作图,图象如图所示.
(1)由图象可以得出图线的函数表达式为F=(30L-1.8) N;
(2)图线的斜率即为弹簧的劲度系数k=30 N/m;
(3)图线与横轴的交点表示弹簧弹力F=0时弹簧的长度,即弹簧的原长;
(4)图线延长后与纵轴的交点表示弹簧长度为5 cm时的弹力,此时弹簧被压缩了1 cm,即表示弹簧被压缩1 cm时的弹力.
【答案】 图线见解析 (1)(30L-1.8) (2)30 (3)见解析 (4)见解析
总结提能 图象法是处理实验数据的一种常用方法,在物理学中经常用图象处理物理问题,解答这类问题时必须明确:(1)图线斜率的物理意义(或切线斜率的物理意义);(2)图线与纵轴、横轴交点的物理意义.
以下是一位同学做“探究弹簧弹力与弹簧伸长量的关系”的实验.
(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,用字母排列出来:CBDAEF.
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数
据(x,F)对应的点,并用平滑的曲线连接起来
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0
C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺
D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码
E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式
F.解释函数表达式中常数的物理意义
(2)下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据:
弹簧的弹力(F/N) 0.5 1.0 1.5 2.0 2.5
弹簧的原长度(L0/cm) 15 15 15 15 15
弹簧的长度(L/cm) 16.2 17.3 18.5 19.6 20.8
弹簧的伸长量(x/cm)
①写出曲线的函数表达式(x用cm作单位):F=0.43x.
②函数表达式中常数的物理意义:弹簧的劲度系数.
解析:(1)按实验操作的先后顺序,步骤为:CBDAEF.
(2)①k==0.43 N/cm,得F=0.43x.
②常数为弹簧的劲度系数.
1.(多选)下列各种情况中,属于弹性形变的有( AB )
A.撑竿跳高运动员起跳中,撑竿的形变
B.当你坐在椅子上时,椅面发生的微小形变
C.细钢丝被绕制成弹簧
D.铝桶被砸扁
解析:本题考查对弹性形变的理解.“撑竿的形变”“椅面发生的微小形变”均能恢复原状,是弹性形变;“细钢丝被绕制成弹簧”不能恢复成“钢丝”,“铝桶被砸扁”不能恢复成“桶”,是非弹性形变,故选项A、B正确,C、D错误.
2.体育课上一学生将足球踢向斜台,如图所示.下列关于斜台对足球的弹力的方向,说法正确的是( D )
A.沿v1的方向
B.先沿v1的方向后沿v2的方向
C.沿v2的方向
D.沿垂直于斜台斜向左上方的方向
解析:支持力是弹力,方向总是垂直于接触面,并指向被支持物,所以斜台对足球的弹力方向为垂直于斜台斜向左上方,故D正确.
3.一辆汽车停在水平地面上,下列说法中正确的是( C )
A.地面受到了向下的弹力,是因为地面发生了弹性形变;汽车没有发生形变,所以汽车不受弹力
B.地面受到了向下的弹力,是因为地面发生了弹性形变;汽车受到了向上的弹力,是因为汽车也发生了形变
C.汽车受到向上的弹力,是因为地面发生了形变;地面受到向下的弹力,是因为汽车发生了形变
D.以上说法都不正确
解析:汽车停在水平地面上,汽车受到的弹力是因为地面发生了形变而又要恢复原状从而对阻碍其恢复的物体产生的作用力;地面受到的弹力是由于汽车发生了形变又要恢复原状从而对阻碍其恢复的地面产生的作用力,故选项C正确,A、B、D错误.
4.在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如下图(1)所示连接起来进行探究.
钩码数 1 2 3 4
LA/cm 15.71 19.71 23.66 27.76
LB/cm 29.96 35.76 41.51 47.36
(1)某次测量如下图(2)所示,指针示数为16.00 cm.
(2)在弹性限度内,将50 g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如上表.用表中数据计算弹簧Ⅰ的劲度系数为12.45 N/m(重力加速度g=10 m/s2),由表中数据能(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数.
解析:(1)指针示数为160.0 mm=16.00 cm.(2)由3mg=k1(LA4-LA1)解得k1== N/m≈12.45 N/m.同理也能计算出弹簧Ⅱ的劲度系数.
5.请在下图中画出杆或球所受的弹力.
(a)杆靠在墙上;
(b)杆放在半球形的槽中;
(c)球用细线悬挂在竖直墙上;
(d)点1、2、3都可能是球的重心位置,点2是球心,点1、2、3在同一竖直线上.
解析:本题考查对弹力方向的判定,关键是熟悉各种接触中的弹力方向.
(a)杆在重力作用下对A、B两处都产生挤压作用,故A、B两处对杆都有弹力,弹力方向与接触点的平面垂直.如图(a)所示.
(b)杆对C、D两处都有挤压作用,因C处为曲面,D处为支撑点,所以C处弹力垂直于其切面指向球心,D处弹力垂直于杆斜向上.如图(b)所示.
(c)球挤压墙壁且拉紧绳子,所以墙对球的弹力与墙面垂直;绳子对球的弹力沿绳子斜向上.如图(c)所示.
(d)当重心不在球心处时,弹力作用也必通过球心点2,如图(d)所示.应注意不要错误地认为弹力作用线必定通过球的重心.
答案:图见解析
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
