高中物理人教版选修3-1学案 2.6 导体的电阻 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3-1学案 2.6 导体的电阻 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 524.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-03 15:23:29 | ||
图片预览




文档简介
6 导体的电阻
你能否依据电阻定律说明:几个电阻串联,总电阻增大,几个电阻并联,总电阻变小?
提示:几个电阻串联相当于增大了导体的长度,几个电阻并联相当于增大了导体的横截面积.
【例1】 两根完全相同的金属裸导线,如果把其中的一根均匀地拉长到原来的两倍,把另一根导线对折后绞合起来,则它们的电阻之比为多少?
导线的长度和横截面积变化后,总体积并没有变化.
【答案】 16?1
【解析】 金属裸导线原来的电阻为R=ρ,拉长后l′=2l,又因为体积V=lS不变,
所以S′=,所以R′=ρ=4ρ=4R,
对折后l″=,S″=2S,
所以R″=ρ=ρ=,
所以R′?R″=16?1.
总结提能 应用电阻定律解题,一般电阻率ρ不变,理解l、S的意义是关键.若导体的长度拉伸为原来的n倍,因导体的体积不变,横截面积必减为原来的;若导体长度压缩为原来的(相当于对折为等长的n根),横截面积变为原来的n倍,长度变为原来的.然后由电阻定律知道电阻变为原来的n2倍或倍.
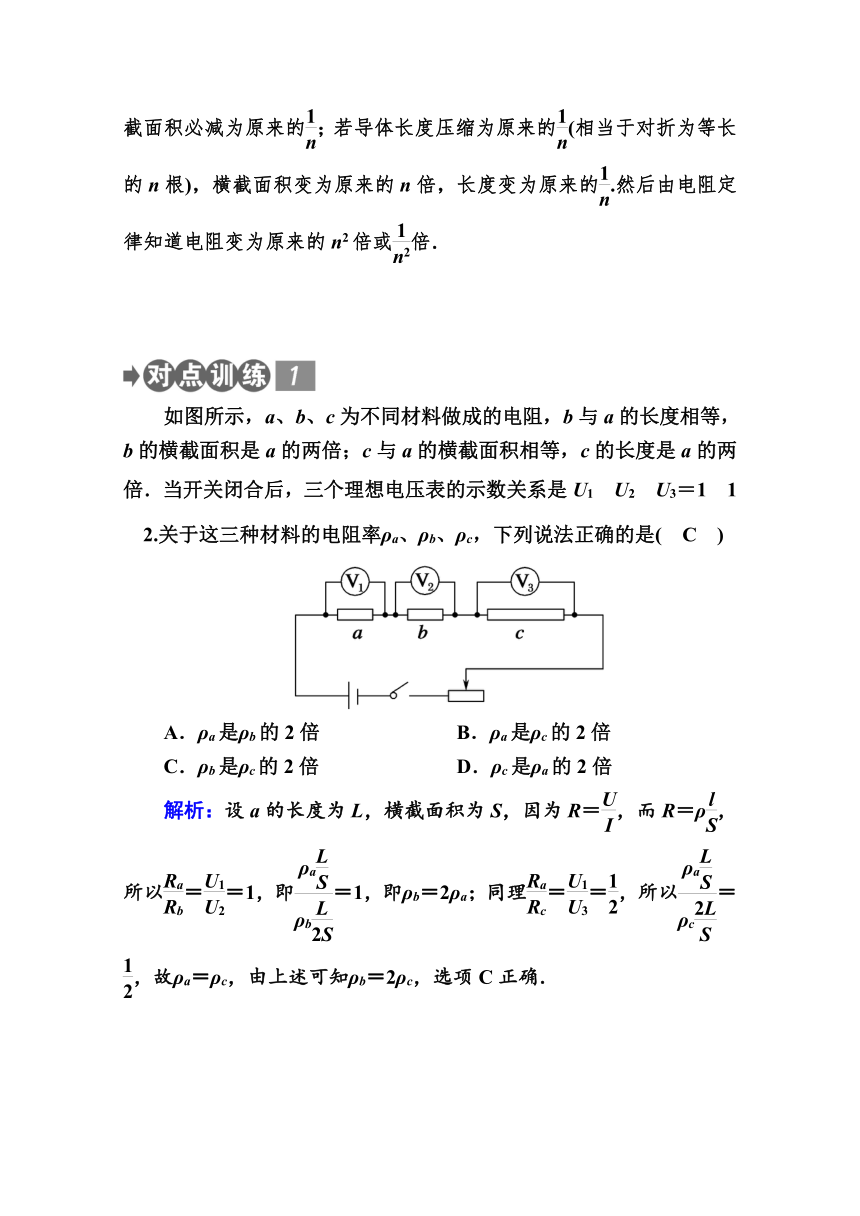
如图所示,a、b、c为不同材料做成的电阻,b与a的长度相等,b的横截面积是a的两倍;c与a的横截面积相等,c的长度是a的两倍.当开关闭合后,三个理想电压表的示数关系是U1?U2?U3=1?1?2.关于这三种材料的电阻率ρa、ρb、ρc,下列说法正确的是( C )
A.ρa是ρb的2倍 B.ρa是ρc的2倍
C.ρb是ρc的2倍 D.ρc是ρa的2倍
解析:设a的长度为L,横截面积为S,因为R=,而R=ρ,所以==1,即=1,即ρb=2ρa;同理==,所以=,故ρa=ρc,由上述可知ρb=2ρc,选项C正确.
考点二 电阻与电阻率的比较
1.电阻与电阻率的比较
电阻R 电阻率ρ
描述对象 导体 材料
物理意义 反映导体对电流阻碍作用的大小,R大,阻碍作用大 反映材料导电性能的好坏,ρ大,导电性能差
决定因素 由材料、温度和导体形状决定 由材料、温度决定,与导体形状无关
单位 欧姆(Ω) 欧姆·米(Ω·m)
联系 R=ρ,ρ大,R不一定大,导体对电流阻碍作用不一定大;R大,ρ不一定大,导电性能不一定差
各种材料的电阻率一般都随温度的变化而变化
(1)金属的电阻率随温度的升高而增大.
(2)半导体(热敏电阻)的电阻率随温度的升高而减小.
2.电阻定律与欧姆定律相结合解决实际问题
电阻定律与欧姆定律相结合的问题在生产、生活、科技实践中有着广泛的应用.解决此类问题,首先要明确R=ρ中各量的含义和电路中电流、电压的关系;其次,要根据题意建立起相应的物理模型,再运用有关的规律进行求解.
【例2】 A、B两地相距40 km,从A到B两条输电线的总电阻为800 Ω.若在A、B之间的某处C两条线路发生短路,为查明短路地点,在A处接上电源,测得A处两端电压为10 V,导线中电流为40 mA.求短路处距A多远?
解答本题时应注意运用导体电阻与长度的关系,根据欧姆定律和电阻定律列式求解.
【答案】 12.5 km
【解析】 根据题意,画出如图所示的电路,A、B两地相距L1=40 km,原输电线总长为2L1=80 km,电阻R1=800 Ω.
设短路处C距A处的距离为L2,其间输电线总电阻为R2,则有R2== Ω=250 Ω
由电阻定律得=所以L2=L1=12.5 km,
即C处距A处的距离为12.5 km.
某电路需要20 A的保险丝,但手边只有用同种材料制成的“15 A”和“5 A”两种型号的保险丝,它们的规格如下表所示,问能否将这两种保险丝取等长的两段并联后接入该电路中?说明其理由.
保险丝 1 2
直径 1 mm 2 mm
额定电流 5 A 15 A
答案:见解析
解析:这两段等长的保险丝横截面积之比S1S2=14,由电阻定律R=ρ得电阻之比R1R2=S2S1=41,并联接入电路后两端的电压相等,由欧姆定律得通过的电流之比I1I2=R2R1=14,即第2根保险丝中的实际电流是第1根中的4倍,而额定电流只是第1根的3倍,所以不能这样来使用.
考点三 实验:测定金属的电阻率
一、实验目的
1.学会使用电流表和电压表以及正确读数.
2.学会使用螺旋测微器以及正确读数.
3.掌握测定金属电阻率的方法.
二、实验原理
1.螺旋测微器
(1)构造原理:螺旋测微器是测量长度的仪器之一.在实验中常用它测量小球的直径、金属丝的直径和薄板的厚度等.用它测量长度,可以精确到0.01 mm,还可以估读到0.001 mm(即毫米的千分位),因此螺旋测微器又称为千分尺.
下图所示是常用的螺旋测微器.它的小砧A和固定刻度B固定在框架C上,旋钮D、微调旋钮D′和可动刻度E、测微螺杆F连在一起,通过精密螺纹套在B上.精密螺纹的螺距是0.5 mm,即每旋转一周,F前进或后退0.5 mm.可动刻度分成50等份,每一等份表示0.01 mm,即可动刻度每转过1等份,F前进或后退0.01 mm,因此,从可动刻度旋转了多少个等份就知道长度变化了多少个0.01 mm.
(2)使用方法:a.找出零误差.测物前将两小砧并拢,如果可动刻度的零刻线正好在固定的零刻线上,零误差为零;如果可动刻度的零刻线在固定零刻线之上n小格,应在读数中加上0.01×n (mm),反之则减去0.01×n (mm).
b.将待测物体放在两小砧之间,旋动旋钮直至可动小砧快靠近被测物体时,改用微调调至可动小砧紧靠物体,听到“咔咔……”声后,止动,即可读数.
c.待测物体长度的整的毫米数从固定刻度上读出,小数部分由可动刻度读出.
(3)注意事项:
a.读数时要注意固定刻度尺上表示半毫米的刻度线是否已经露出.
b.由螺旋测微器读数时必须估读一位,即估读到0.001 mm这一位上.
2.测金属丝电阻率的原理
用毫米刻度尺测一段金属导线的长度l,用螺旋测微器测导线的直径d,用伏安法(因金属导线电阻较小采用外接法)测导线的电阻R,由R=ρ,得ρ==,实验电路如图所示.
三、实验器材
直流电流表(0~0.6 A)、直流电压表(0~3 V)、电池(3 V)、滑动变阻器(0~10 Ω)、长约1 m的金属丝、开关1只、导线若干、毫米刻度尺、螺旋测微器.
四、实验步骤
1.用毫米刻度尺测量金属丝的长度l,测三次取平均值.
2.用螺旋测微器测量金属丝的直径,在不同位置,测量三次,取平均值,并算出金属丝的横截面积S.
3.把金属丝接入电路中,调节滑动变阻器的阻值,测得三组U、I数据,分别求出每组数据所对应的电阻值R1、R2、R3,取平均值R=作为金属丝的电阻.
4.用公式ρ=求得该金属丝的电阻率.
五、注意事项
1.为了方便,应在金属导线连入电路前测导线直径,为了准确,应测量拉直悬空的连入电路的导线的有效长度,且各测量三次,取平均值.
2.测量电路应选用电流表外接法,且测电阻时,电流不宜过大,通电时间不宜太长,因为电阻率随温度而改变.
3.为准确求出R的平均值,应多测几组U、I数值,然后采用U?I图象法求出电阻.
4.滑动变阻器用限流式接法就可以满足该实验的要求.
六、误差分析
1.测量误差:测量金属丝的直径、长度以及电流、电压时出现读数误差.
2.由于采用电流表外接法,电压表的分流,造成电阻测量值偏小(若误用内接法,则电流表分压影响更大).
3.通电电流太大,或时间太长,致使金属丝发热,电阻率随之变化.
【例3】 在做“测定金属的电阻率”的实验时,需要对金属丝的电阻进行测量,已知金属丝的电阻值Rx,约为20 Ω.一位同学用伏安法对这个电阻的阻值进行了比较精确的测量,这位同学想使被测电阻Rx两端的电压变化范围尽可能大.他可选用的器材有:
电源E:电动势为8 V,内阻为1.0 Ω;
电流表A:量程0.6 A,内阻约为0.50 Ω;
电压表V:量程10 V,内阻约为10 kΩ;
滑动变阻器R:最大电阻值为5.0 Ω;
开关一个,导线若干.
(1)根据上述条件,测量时电流表应采用________(选填“外接法”或“内接法”).
(2)在方框内画出实验电路图.
(3)若在上述实验中,电流表的示数为I,电压表的示数为U,且电流表内阻RA电压表内阻RV均为已知量,用测量物理量和电表内阻计算金属丝电阻的表达式.
Rx=________.
解答本题时注意把握以下两点:
(1)要使被测电阻Rx两端的电压变化范围尽量大,就要采用滑动变阻器的分压式接法.
(2)电流表、电压表的内阻为已知量时相当于一个特殊电阻.
【答案】 (1)外接法 (2)见解析图 (3)
【解析】 (1)待测电阻约为20 Ω,是电流表内阻的40倍,但电压表内阻是待测电阻的500倍,故采用外接法.
(2)因为要使Rx两端的电压变化范围尽可能大,所以滑动变阻器要采用分压式,电路图如图所示.
(3)电压表分得的电流为IV=,所以Rx中的电流为Ix=I-IV=I-,则Rx===.
总结提能 当电压表、电流表的内阻已知时,它们就相当于一个电阻,其两端的电压和流过的电流和它本身的电阻三者满足欧姆定律.
某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图甲、乙、丙所示,则它们的读数值依次是0.999_mm(0.998~1.000_mm)、0.42_A、2.16_V(2.15~2.17_V).
(1)已知实验中所用的滑动变阻器阻值范围为0~10 Ω,电流表内阻约几欧,电压表内阻约20 kΩ.电源为干电池(不宜在长时间、大功率状况下使用),电动势E=4.5 V,内阻很小.则下列选项电路图中A(填电路图下方的字母代号)电路为本次实验应当采用的最佳电路.但用此最佳电路测量的结果仍然会比真实值偏小.
(2)若已知实验所用的电流表内阻的准确值RA=2.0 Ω,那么准确测量金属丝电阻Rx的最佳电路应是上述选项图中的B电路(填电路图下的字母代号).此时测得电流为I、电压为U,则金属丝电阻Rx=-RA(用题中字母代号表示).
(3)为了完成整个实验,还需要测量接入电路中的电阻丝长度l,所用到的仪器是刻度尺,测量电阻率的公式是ρ=.(用测量的物理量表示)
解析:螺旋测微器的主尺刻度为0.5 mm,螺旋尺刻度数为49.9,螺旋测微器的最小分度值为0.01 mm,故螺旋测微器的读数为0.999 mm.电流表读数为0.42 A(同位估读),电压表读数为2.16 V(下一位估读).
(1)根据题意,因为电源不宜在长时间、大功率状况下使用,所以应选择滑动变阻器限流式,被测电阻阻值较小,应选用电流表外接法,故选A图,此时测量结果仍然会比真实值偏小.
(2)若已知电流表内阻,则可选用电流表内接法的B图精确测量,分析电路可知Rx=-RA.
(3)测量电阻丝长度的仪器是刻度尺.由电阻率R=ρ,S=πd2,R=,可得电阻率ρ=.
1.有两个同种材料制成的导体,两导体均为横截面为正方形的柱体,柱体高均为h,大柱体柱截面边长为a,小柱体柱截面边长为b,则( C )
A.从图示电流方向看大柱体与小柱体的电阻之比为a?b
B.若电流方向竖直向下,大柱体与小柱体的电阻之比为a?b
C.从图示电流方向看大柱体与小柱体的电阻之比为1?1
D.若电流方向竖直向下,大柱体与小柱体的电阻之比为a2?b2
解析:从图示电流方向看,根据电阻定律有R1==,R2==,则两柱体电阻之比为1?1,故A错误,C正确;若电流竖直向下,根据电阻定律有R1=,R2=,则R1?R2=b2?a2,故B、D错误.
2.(多选)下列说法中正确的是( BD )
A.由R=可知,电阻与电压、电流都有关系
B.由R=ρ可知,电阻与导体的长度和横截面积都有关系
C.各种材料的电阻率都与温度有关,金属的电阻率随温度的升高而减小
D.所谓超导体,当其温度降低到接近绝对零度的某个临界温度时,它的电阻率突然变为零
解析:R=是电阻的定义式,R与电压和电流无关,故A错误;而R=ρ是电阻的决定式,横截面积一定,电阻与导体的长度成正比,长度一定,电阻与导体的横截面积成反比,故B正确;电阻率都与温度有关,金属的电阻率随温度的升高而增大,故C错误;当温度降低到接近绝对零度的某个临界温度时,导体的电阻率突然变为零的现象叫超导现象,此时的导体叫超导体,故D正确.
3.一只“220 V 100 W”的灯泡工作时电阻为484 Ω,拿一只同样的灯泡来测量它不工作时的电阻,下列说法中正确的是( A )
A.小于484 Ω B.大于484 Ω
C.等于484 Ω D.无法确定
解析:灯泡工作时的电阻为高温状态的电阻,不工作时为常温下的电阻,根据金属材料的电阻随温度的升高而增大可得选项A正确.
4.某研究小组要测定一铭牌上只有额定电压为10 V、而其他字迹不清楚的直流电动机正常工作时的机械功率,实验室提供的器材有电流表、电压表、滑动变阻器(阻值较小),备用电池若干,开关、若干导线、细线、重物.
(1)小组成员设计如图甲、乙所示两个测量电路,其中比较合理的是乙图.(填写“甲”或“乙”)
(2)根据选取的电路图完善下图中用电动机提升重物的实物电路连接.
答案:
(3)闭合开关前应将丙图中的滑动变阻器的滑片移到最左端(填“左”或“右”).闭合开关后移动滑动变阻器,使电压表和电流表都有明显的示数,但电动机并未转动,读出此时电压表和电流表的示数分别为2 V,1 A,继续移动滑动变阻器的滑片,将电压表的示数调为10 V,这时电流表的示数为0.4 A,重物恰好匀速上升,此时电动机输出的机械功率为3.68 W,若重物重为8 N,则重物匀速上升的速度大小为0.46 m/s.
解析:(1)因滑动变阻器的阻值较小,为使电压表与电流表的示数变化范围较大,滑动变阻器应采用分压接法,故选择图乙所示电路.(2)根据电路图连接实物电路,实物电路如答图所示.(3)滑动变阻器采用分压接法,为保护电路,闭合开关前应将丙图中的滑动变阻器的滑片移到最左端.闭合开关后移动滑动变阻器,电动机并未转动,读出此时电压表和电流表的示数分别为2.0 V,1.0 A,电动机内阻为:r===2 Ω.电动机在额定电压10.0 V下正常工作,此时电流表的示数为0.4 A,电动机的总功率为:P=UI=10 V×0.4 A=4 W,电动机的热功率:P热=I2r=0.32 W,此时电动机输出的机械功率:P机械=P-P热=4 W-0.32 W=3.68 W,P机械=Fv=Gv,重物匀速上升时的速度大小:v==0.46 m/s.
5.工业上采用的一种称为“电导仪”的仪器,其中一个关键部件如图所示,A、B是两片面积为1 cm2的正方形铂片,间距为d=1 cm,把它们浸在待测液体中,若通过两根引线加上一定的电压U=6 V时,测出电流I=1 μA,则这种液体的电阻率为多少?
答案:6×104 Ω·m
解析:R== Ω=6×106 Ω
由题意知l=d=10-2 m,S=10-4 m2
由R=ρ得ρ== Ω·m
=6×104 Ω·m.
你能否依据电阻定律说明:几个电阻串联,总电阻增大,几个电阻并联,总电阻变小?
提示:几个电阻串联相当于增大了导体的长度,几个电阻并联相当于增大了导体的横截面积.
【例1】 两根完全相同的金属裸导线,如果把其中的一根均匀地拉长到原来的两倍,把另一根导线对折后绞合起来,则它们的电阻之比为多少?
导线的长度和横截面积变化后,总体积并没有变化.
【答案】 16?1
【解析】 金属裸导线原来的电阻为R=ρ,拉长后l′=2l,又因为体积V=lS不变,
所以S′=,所以R′=ρ=4ρ=4R,
对折后l″=,S″=2S,
所以R″=ρ=ρ=,
所以R′?R″=16?1.
总结提能 应用电阻定律解题,一般电阻率ρ不变,理解l、S的意义是关键.若导体的长度拉伸为原来的n倍,因导体的体积不变,横截面积必减为原来的;若导体长度压缩为原来的(相当于对折为等长的n根),横截面积变为原来的n倍,长度变为原来的.然后由电阻定律知道电阻变为原来的n2倍或倍.
如图所示,a、b、c为不同材料做成的电阻,b与a的长度相等,b的横截面积是a的两倍;c与a的横截面积相等,c的长度是a的两倍.当开关闭合后,三个理想电压表的示数关系是U1?U2?U3=1?1?2.关于这三种材料的电阻率ρa、ρb、ρc,下列说法正确的是( C )
A.ρa是ρb的2倍 B.ρa是ρc的2倍
C.ρb是ρc的2倍 D.ρc是ρa的2倍
解析:设a的长度为L,横截面积为S,因为R=,而R=ρ,所以==1,即=1,即ρb=2ρa;同理==,所以=,故ρa=ρc,由上述可知ρb=2ρc,选项C正确.
考点二 电阻与电阻率的比较
1.电阻与电阻率的比较
电阻R 电阻率ρ
描述对象 导体 材料
物理意义 反映导体对电流阻碍作用的大小,R大,阻碍作用大 反映材料导电性能的好坏,ρ大,导电性能差
决定因素 由材料、温度和导体形状决定 由材料、温度决定,与导体形状无关
单位 欧姆(Ω) 欧姆·米(Ω·m)
联系 R=ρ,ρ大,R不一定大,导体对电流阻碍作用不一定大;R大,ρ不一定大,导电性能不一定差
各种材料的电阻率一般都随温度的变化而变化
(1)金属的电阻率随温度的升高而增大.
(2)半导体(热敏电阻)的电阻率随温度的升高而减小.
2.电阻定律与欧姆定律相结合解决实际问题
电阻定律与欧姆定律相结合的问题在生产、生活、科技实践中有着广泛的应用.解决此类问题,首先要明确R=ρ中各量的含义和电路中电流、电压的关系;其次,要根据题意建立起相应的物理模型,再运用有关的规律进行求解.
【例2】 A、B两地相距40 km,从A到B两条输电线的总电阻为800 Ω.若在A、B之间的某处C两条线路发生短路,为查明短路地点,在A处接上电源,测得A处两端电压为10 V,导线中电流为40 mA.求短路处距A多远?
解答本题时应注意运用导体电阻与长度的关系,根据欧姆定律和电阻定律列式求解.
【答案】 12.5 km
【解析】 根据题意,画出如图所示的电路,A、B两地相距L1=40 km,原输电线总长为2L1=80 km,电阻R1=800 Ω.
设短路处C距A处的距离为L2,其间输电线总电阻为R2,则有R2== Ω=250 Ω
由电阻定律得=所以L2=L1=12.5 km,
即C处距A处的距离为12.5 km.
某电路需要20 A的保险丝,但手边只有用同种材料制成的“15 A”和“5 A”两种型号的保险丝,它们的规格如下表所示,问能否将这两种保险丝取等长的两段并联后接入该电路中?说明其理由.
保险丝 1 2
直径 1 mm 2 mm
额定电流 5 A 15 A
答案:见解析
解析:这两段等长的保险丝横截面积之比S1S2=14,由电阻定律R=ρ得电阻之比R1R2=S2S1=41,并联接入电路后两端的电压相等,由欧姆定律得通过的电流之比I1I2=R2R1=14,即第2根保险丝中的实际电流是第1根中的4倍,而额定电流只是第1根的3倍,所以不能这样来使用.
考点三 实验:测定金属的电阻率
一、实验目的
1.学会使用电流表和电压表以及正确读数.
2.学会使用螺旋测微器以及正确读数.
3.掌握测定金属电阻率的方法.
二、实验原理
1.螺旋测微器
(1)构造原理:螺旋测微器是测量长度的仪器之一.在实验中常用它测量小球的直径、金属丝的直径和薄板的厚度等.用它测量长度,可以精确到0.01 mm,还可以估读到0.001 mm(即毫米的千分位),因此螺旋测微器又称为千分尺.
下图所示是常用的螺旋测微器.它的小砧A和固定刻度B固定在框架C上,旋钮D、微调旋钮D′和可动刻度E、测微螺杆F连在一起,通过精密螺纹套在B上.精密螺纹的螺距是0.5 mm,即每旋转一周,F前进或后退0.5 mm.可动刻度分成50等份,每一等份表示0.01 mm,即可动刻度每转过1等份,F前进或后退0.01 mm,因此,从可动刻度旋转了多少个等份就知道长度变化了多少个0.01 mm.
(2)使用方法:a.找出零误差.测物前将两小砧并拢,如果可动刻度的零刻线正好在固定的零刻线上,零误差为零;如果可动刻度的零刻线在固定零刻线之上n小格,应在读数中加上0.01×n (mm),反之则减去0.01×n (mm).
b.将待测物体放在两小砧之间,旋动旋钮直至可动小砧快靠近被测物体时,改用微调调至可动小砧紧靠物体,听到“咔咔……”声后,止动,即可读数.
c.待测物体长度的整的毫米数从固定刻度上读出,小数部分由可动刻度读出.
(3)注意事项:
a.读数时要注意固定刻度尺上表示半毫米的刻度线是否已经露出.
b.由螺旋测微器读数时必须估读一位,即估读到0.001 mm这一位上.
2.测金属丝电阻率的原理
用毫米刻度尺测一段金属导线的长度l,用螺旋测微器测导线的直径d,用伏安法(因金属导线电阻较小采用外接法)测导线的电阻R,由R=ρ,得ρ==,实验电路如图所示.
三、实验器材
直流电流表(0~0.6 A)、直流电压表(0~3 V)、电池(3 V)、滑动变阻器(0~10 Ω)、长约1 m的金属丝、开关1只、导线若干、毫米刻度尺、螺旋测微器.
四、实验步骤
1.用毫米刻度尺测量金属丝的长度l,测三次取平均值.
2.用螺旋测微器测量金属丝的直径,在不同位置,测量三次,取平均值,并算出金属丝的横截面积S.
3.把金属丝接入电路中,调节滑动变阻器的阻值,测得三组U、I数据,分别求出每组数据所对应的电阻值R1、R2、R3,取平均值R=作为金属丝的电阻.
4.用公式ρ=求得该金属丝的电阻率.
五、注意事项
1.为了方便,应在金属导线连入电路前测导线直径,为了准确,应测量拉直悬空的连入电路的导线的有效长度,且各测量三次,取平均值.
2.测量电路应选用电流表外接法,且测电阻时,电流不宜过大,通电时间不宜太长,因为电阻率随温度而改变.
3.为准确求出R的平均值,应多测几组U、I数值,然后采用U?I图象法求出电阻.
4.滑动变阻器用限流式接法就可以满足该实验的要求.
六、误差分析
1.测量误差:测量金属丝的直径、长度以及电流、电压时出现读数误差.
2.由于采用电流表外接法,电压表的分流,造成电阻测量值偏小(若误用内接法,则电流表分压影响更大).
3.通电电流太大,或时间太长,致使金属丝发热,电阻率随之变化.
【例3】 在做“测定金属的电阻率”的实验时,需要对金属丝的电阻进行测量,已知金属丝的电阻值Rx,约为20 Ω.一位同学用伏安法对这个电阻的阻值进行了比较精确的测量,这位同学想使被测电阻Rx两端的电压变化范围尽可能大.他可选用的器材有:
电源E:电动势为8 V,内阻为1.0 Ω;
电流表A:量程0.6 A,内阻约为0.50 Ω;
电压表V:量程10 V,内阻约为10 kΩ;
滑动变阻器R:最大电阻值为5.0 Ω;
开关一个,导线若干.
(1)根据上述条件,测量时电流表应采用________(选填“外接法”或“内接法”).
(2)在方框内画出实验电路图.
(3)若在上述实验中,电流表的示数为I,电压表的示数为U,且电流表内阻RA电压表内阻RV均为已知量,用测量物理量和电表内阻计算金属丝电阻的表达式.
Rx=________.
解答本题时注意把握以下两点:
(1)要使被测电阻Rx两端的电压变化范围尽量大,就要采用滑动变阻器的分压式接法.
(2)电流表、电压表的内阻为已知量时相当于一个特殊电阻.
【答案】 (1)外接法 (2)见解析图 (3)
【解析】 (1)待测电阻约为20 Ω,是电流表内阻的40倍,但电压表内阻是待测电阻的500倍,故采用外接法.
(2)因为要使Rx两端的电压变化范围尽可能大,所以滑动变阻器要采用分压式,电路图如图所示.
(3)电压表分得的电流为IV=,所以Rx中的电流为Ix=I-IV=I-,则Rx===.
总结提能 当电压表、电流表的内阻已知时,它们就相当于一个电阻,其两端的电压和流过的电流和它本身的电阻三者满足欧姆定律.
某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图甲、乙、丙所示,则它们的读数值依次是0.999_mm(0.998~1.000_mm)、0.42_A、2.16_V(2.15~2.17_V).
(1)已知实验中所用的滑动变阻器阻值范围为0~10 Ω,电流表内阻约几欧,电压表内阻约20 kΩ.电源为干电池(不宜在长时间、大功率状况下使用),电动势E=4.5 V,内阻很小.则下列选项电路图中A(填电路图下方的字母代号)电路为本次实验应当采用的最佳电路.但用此最佳电路测量的结果仍然会比真实值偏小.
(2)若已知实验所用的电流表内阻的准确值RA=2.0 Ω,那么准确测量金属丝电阻Rx的最佳电路应是上述选项图中的B电路(填电路图下的字母代号).此时测得电流为I、电压为U,则金属丝电阻Rx=-RA(用题中字母代号表示).
(3)为了完成整个实验,还需要测量接入电路中的电阻丝长度l,所用到的仪器是刻度尺,测量电阻率的公式是ρ=.(用测量的物理量表示)
解析:螺旋测微器的主尺刻度为0.5 mm,螺旋尺刻度数为49.9,螺旋测微器的最小分度值为0.01 mm,故螺旋测微器的读数为0.999 mm.电流表读数为0.42 A(同位估读),电压表读数为2.16 V(下一位估读).
(1)根据题意,因为电源不宜在长时间、大功率状况下使用,所以应选择滑动变阻器限流式,被测电阻阻值较小,应选用电流表外接法,故选A图,此时测量结果仍然会比真实值偏小.
(2)若已知电流表内阻,则可选用电流表内接法的B图精确测量,分析电路可知Rx=-RA.
(3)测量电阻丝长度的仪器是刻度尺.由电阻率R=ρ,S=πd2,R=,可得电阻率ρ=.
1.有两个同种材料制成的导体,两导体均为横截面为正方形的柱体,柱体高均为h,大柱体柱截面边长为a,小柱体柱截面边长为b,则( C )
A.从图示电流方向看大柱体与小柱体的电阻之比为a?b
B.若电流方向竖直向下,大柱体与小柱体的电阻之比为a?b
C.从图示电流方向看大柱体与小柱体的电阻之比为1?1
D.若电流方向竖直向下,大柱体与小柱体的电阻之比为a2?b2
解析:从图示电流方向看,根据电阻定律有R1==,R2==,则两柱体电阻之比为1?1,故A错误,C正确;若电流竖直向下,根据电阻定律有R1=,R2=,则R1?R2=b2?a2,故B、D错误.
2.(多选)下列说法中正确的是( BD )
A.由R=可知,电阻与电压、电流都有关系
B.由R=ρ可知,电阻与导体的长度和横截面积都有关系
C.各种材料的电阻率都与温度有关,金属的电阻率随温度的升高而减小
D.所谓超导体,当其温度降低到接近绝对零度的某个临界温度时,它的电阻率突然变为零
解析:R=是电阻的定义式,R与电压和电流无关,故A错误;而R=ρ是电阻的决定式,横截面积一定,电阻与导体的长度成正比,长度一定,电阻与导体的横截面积成反比,故B正确;电阻率都与温度有关,金属的电阻率随温度的升高而增大,故C错误;当温度降低到接近绝对零度的某个临界温度时,导体的电阻率突然变为零的现象叫超导现象,此时的导体叫超导体,故D正确.
3.一只“220 V 100 W”的灯泡工作时电阻为484 Ω,拿一只同样的灯泡来测量它不工作时的电阻,下列说法中正确的是( A )
A.小于484 Ω B.大于484 Ω
C.等于484 Ω D.无法确定
解析:灯泡工作时的电阻为高温状态的电阻,不工作时为常温下的电阻,根据金属材料的电阻随温度的升高而增大可得选项A正确.
4.某研究小组要测定一铭牌上只有额定电压为10 V、而其他字迹不清楚的直流电动机正常工作时的机械功率,实验室提供的器材有电流表、电压表、滑动变阻器(阻值较小),备用电池若干,开关、若干导线、细线、重物.
(1)小组成员设计如图甲、乙所示两个测量电路,其中比较合理的是乙图.(填写“甲”或“乙”)
(2)根据选取的电路图完善下图中用电动机提升重物的实物电路连接.
答案:
(3)闭合开关前应将丙图中的滑动变阻器的滑片移到最左端(填“左”或“右”).闭合开关后移动滑动变阻器,使电压表和电流表都有明显的示数,但电动机并未转动,读出此时电压表和电流表的示数分别为2 V,1 A,继续移动滑动变阻器的滑片,将电压表的示数调为10 V,这时电流表的示数为0.4 A,重物恰好匀速上升,此时电动机输出的机械功率为3.68 W,若重物重为8 N,则重物匀速上升的速度大小为0.46 m/s.
解析:(1)因滑动变阻器的阻值较小,为使电压表与电流表的示数变化范围较大,滑动变阻器应采用分压接法,故选择图乙所示电路.(2)根据电路图连接实物电路,实物电路如答图所示.(3)滑动变阻器采用分压接法,为保护电路,闭合开关前应将丙图中的滑动变阻器的滑片移到最左端.闭合开关后移动滑动变阻器,电动机并未转动,读出此时电压表和电流表的示数分别为2.0 V,1.0 A,电动机内阻为:r===2 Ω.电动机在额定电压10.0 V下正常工作,此时电流表的示数为0.4 A,电动机的总功率为:P=UI=10 V×0.4 A=4 W,电动机的热功率:P热=I2r=0.32 W,此时电动机输出的机械功率:P机械=P-P热=4 W-0.32 W=3.68 W,P机械=Fv=Gv,重物匀速上升时的速度大小:v==0.46 m/s.
5.工业上采用的一种称为“电导仪”的仪器,其中一个关键部件如图所示,A、B是两片面积为1 cm2的正方形铂片,间距为d=1 cm,把它们浸在待测液体中,若通过两根引线加上一定的电压U=6 V时,测出电流I=1 μA,则这种液体的电阻率为多少?
答案:6×104 Ω·m
解析:R== Ω=6×106 Ω
由题意知l=d=10-2 m,S=10-4 m2
由R=ρ得ρ== Ω·m
=6×104 Ω·m.
