反比例函数
图片预览




文档简介
(共15张PPT)
反 比 例 函 数
怀宁县高河镇初级中学 丁 青
问题1.某村有耕地200hm2,人口数量x逐年发生变化,该村人均耕地面积yhm2与人口数量x之间有怎么样的关系?
问题2.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场,设它的一边长为a米,求另一边的长b米与a米的关系式?
问题3.高河到安庆距离为40km,一辆汽车跑完全程所需的时间th与行驶的平均速度vkm/h之间有怎样的关系?
1. 反比例函数的定义:
3.它的三种常见的表达形式:
2. 反比例函数的特征:
k ≠0, x ≠0 , y≠0 , x是-1次
xy = k(k ≠ 0)
y=kx-1(k≠0)
一般地,形如
的函数叫做反比例函数.
1、下列函数中哪些是y关于x的反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y =
3
2x
y =
1
3x
y = 2x-1
xy =
4
1
练一练
x
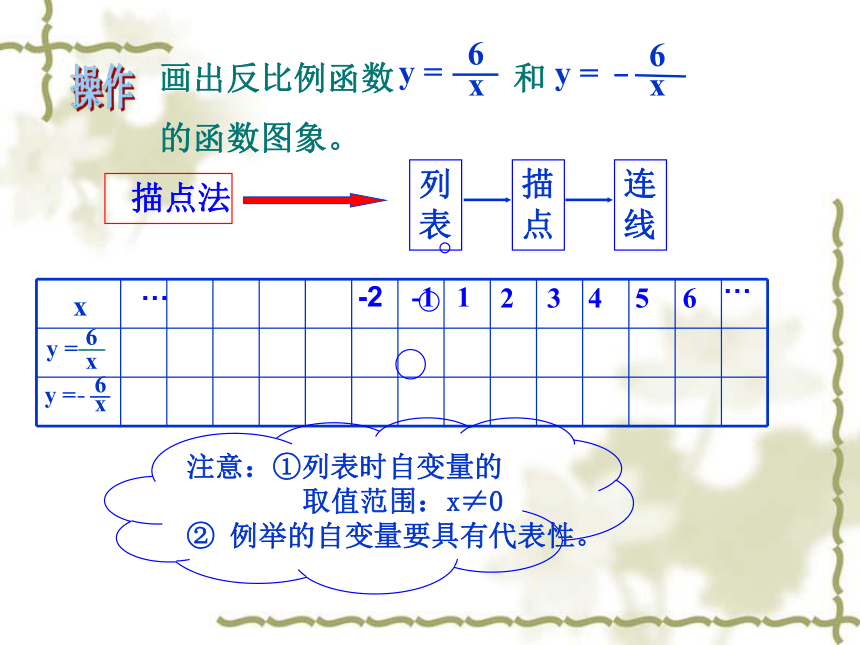
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量的
取值范围:x≠0
② 例举的自变量要具有代表性。
1
2
3
4
5
6
-1
…
-2
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
x
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
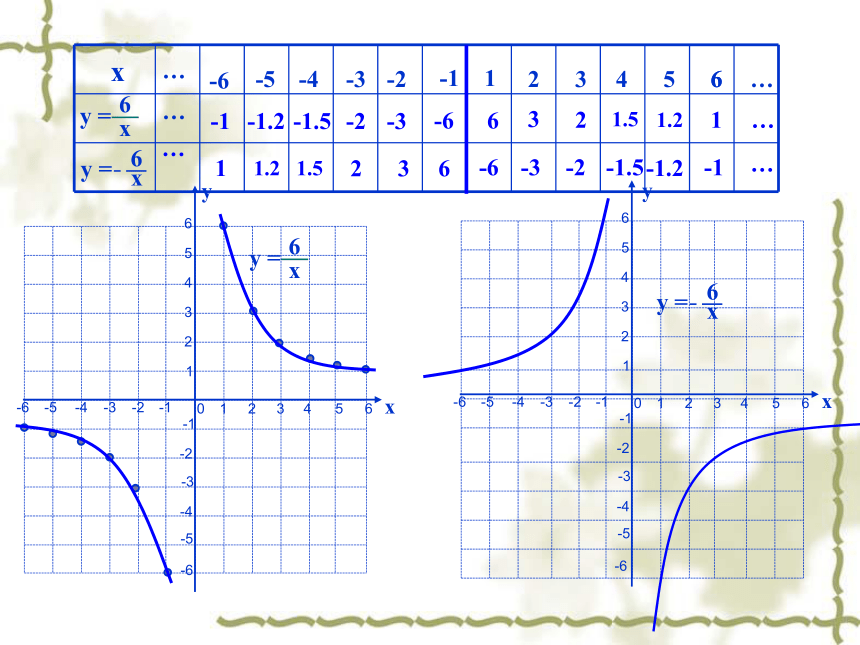
y =
x
6
y =
x
6
y =
x
6
y =
x
6
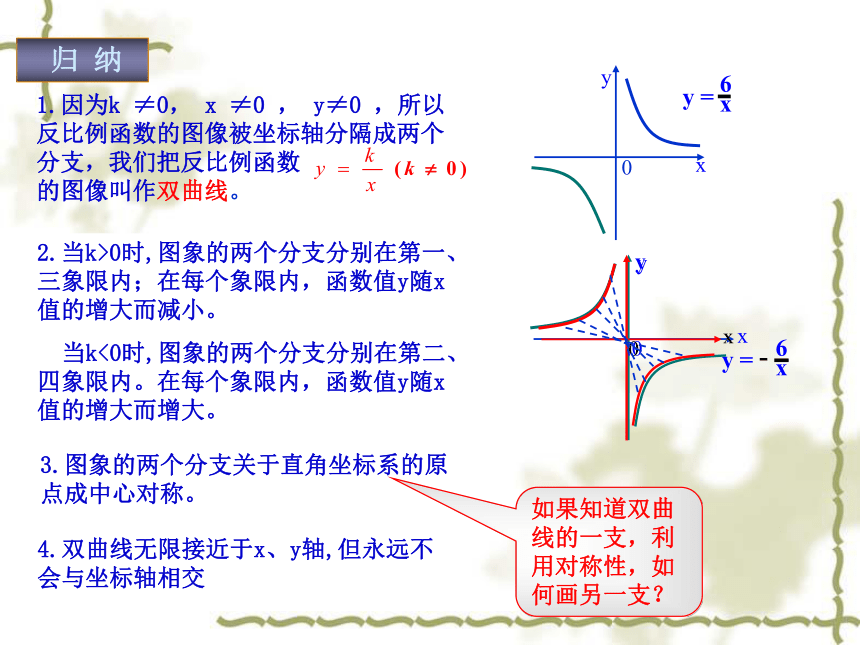
归 纳
2.当k>0时,图象的两个分支分别在第一、三象限内;在每个象限内,函数值y随x值的增大而减小。
当k<0时,图象的两个分支分别在第二、四象限内。在每个象限内,函数值y随x值的增大而增大。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
1.因为k ≠0, x ≠0 , y≠0 ,所以反比例函数的图像被坐标轴分隔成两个分支,我们把反比例函数 的图像叫作双曲线。
1.函数 是 函数,其图象为 , 其中k= ,自变量x的取值范围为 .
反比例
双曲线
2
x≠ 0
练一练
2.对于函数
当x>0时, y的值随x的增大而 ,
当x<0时, y的值随x的增大而 .
增大
增大
练一练
3.若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
4、以下各图表示正比例函数y=kx与反比例函数
的大致图像,其中正确的是 ( )
y
x
o
x
y
o
y
x
o
x
o
y
(A)
(B)
(C)
(D)
练一练
B
5.图是反比例函数y= 的图象的一支.根据图象回答下列问题:
(1)图象的另一支在哪个象限
常数m的取值范围是什么
(2)在这个函数图象的某一支
上任取点A(a,b)和点B(a’,b’).
如果a﹥a’,那么b和b’
有怎么的大小关系
m-5
x
x
y
0
a
a’
b’
b
A
B
练一练
你能总结一下反比例函数的图象性质特征吗
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
图像的两个分支关于原点成中心对称
形状
位置
变化趋势
对称性
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会
与坐标轴相交
K<0
K<0
K>0
K>0
o
x
y
o
x
y
x取不为0的
所有实数
o
x
y
o
x
y
y随着x
增大而
增大
y随着x
增大而
减小
在每一象限
内, y随着
x增大而增大
在每一象限
内,y随着
x增大而减小
y=kx(k≠0)
x取一切实数
反比例函数
正比例函数
性
质
图
像
函数解析式和自变量取值范围
函数名称
谢谢!
反 比 例 函 数
怀宁县高河镇初级中学 丁 青
问题1.某村有耕地200hm2,人口数量x逐年发生变化,该村人均耕地面积yhm2与人口数量x之间有怎么样的关系?
问题2.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场,设它的一边长为a米,求另一边的长b米与a米的关系式?
问题3.高河到安庆距离为40km,一辆汽车跑完全程所需的时间th与行驶的平均速度vkm/h之间有怎样的关系?
1. 反比例函数的定义:
3.它的三种常见的表达形式:
2. 反比例函数的特征:
k ≠0, x ≠0 , y≠0 , x是-1次
xy = k(k ≠ 0)
y=kx-1(k≠0)
一般地,形如
的函数叫做反比例函数.
1、下列函数中哪些是y关于x的反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y =
3
2x
y =
1
3x
y = 2x-1
xy =
4
1
练一练
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量的
取值范围:x≠0
② 例举的自变量要具有代表性。
1
2
3
4
5
6
-1
…
-2
…
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
x
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
y =
x
6
y =
x
6
归 纳
2.当k>0时,图象的两个分支分别在第一、三象限内;在每个象限内,函数值y随x值的增大而减小。
当k<0时,图象的两个分支分别在第二、四象限内。在每个象限内,函数值y随x值的增大而增大。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
1.因为k ≠0, x ≠0 , y≠0 ,所以反比例函数的图像被坐标轴分隔成两个分支,我们把反比例函数 的图像叫作双曲线。
1.函数 是 函数,其图象为 , 其中k= ,自变量x的取值范围为 .
反比例
双曲线
2
x≠ 0
练一练
2.对于函数
当x>0时, y的值随x的增大而 ,
当x<0时, y的值随x的增大而 .
增大
增大
练一练
3.若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
4、以下各图表示正比例函数y=kx与反比例函数
的大致图像,其中正确的是 ( )
y
x
o
x
y
o
y
x
o
x
o
y
(A)
(B)
(C)
(D)
练一练
B
5.图是反比例函数y= 的图象的一支.根据图象回答下列问题:
(1)图象的另一支在哪个象限
常数m的取值范围是什么
(2)在这个函数图象的某一支
上任取点A(a,b)和点B(a’,b’).
如果a﹥a’,那么b和b’
有怎么的大小关系
m-5
x
x
y
0
a
a’
b’
b
A
B
练一练
你能总结一下反比例函数的图象性质特征吗
图象是双曲线
当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内
图像的两个分支关于原点成中心对称
形状
位置
变化趋势
对称性
形 状
位 置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会
与坐标轴相交
K<0
K<0
K>0
K>0
o
x
y
o
x
y
x取不为0的
所有实数
o
x
y
o
x
y
y随着x
增大而
增大
y随着x
增大而
减小
在每一象限
内, y随着
x增大而增大
在每一象限
内,y随着
x增大而减小
y=kx(k≠0)
x取一切实数
反比例函数
正比例函数
性
质
图
像
函数解析式和自变量取值范围
函数名称
谢谢!
