吉林省第二实验学校2020-2021学年第一学期八年级(五四制)第一次月考数学试题(word版,无答案)
文档属性
| 名称 | 吉林省第二实验学校2020-2021学年第一学期八年级(五四制)第一次月考数学试题(word版,无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 17:45:12 | ||
图片预览

文档简介
2020-2021学年第一学期八年级(五四制)第一次月考
数学试题
一.选择题(共8小题)
1.下列算式中,正确的是( )
A.=±5 B.±=3 C.=﹣2 D.=﹣1
2.a12可以写成( )
A.a6+a6 B.a2?a6 C.a6?a6 D.a12÷a
3.计算的结果为( )
A.10 B.5 C.3 D.2
4.如图,△ABC中,∠B=90°,BC=3,AC=4,则AB的长度为( )
A.2 B. C.2 D.5
5.用反证法证明“a<1”,应先假设( )
A.a≥1 B.a>1 C.a=1 D.a≠1
6.在△ABC中,AB=AC,∠B=70°,则∠A的度数是( )
A.40° B.55° C.65° D.60°
7.已知:∠AOB.求作:一个角,使它等于∠AOB.步骤如下:如图,
(1)作射线O'A'
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.则∠A'O'B'就是所求作的角.
请回答:该作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
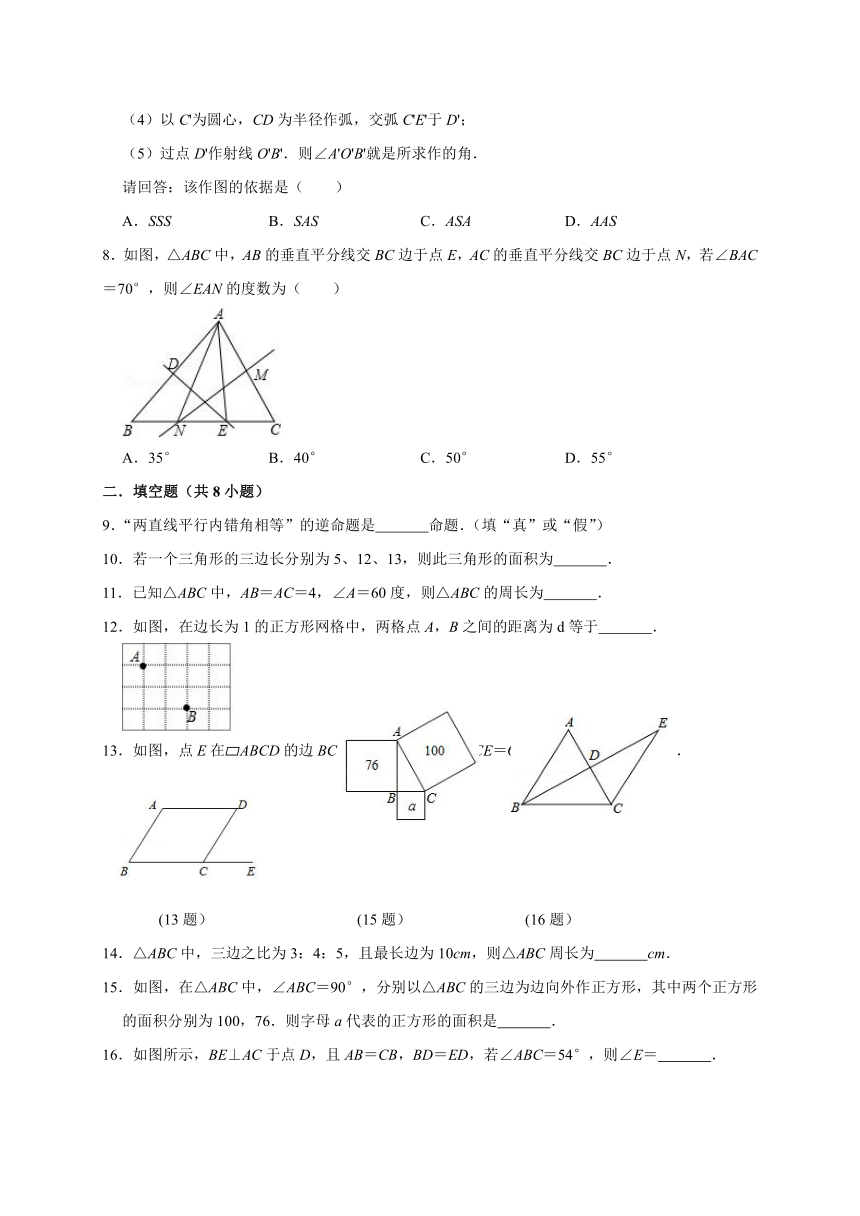
8.如图,△ABC中,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,若∠BAC=70°,则∠EAN的度数为( )
A.35° B.40° C.50° D.55°
二.填空题(共8小题)
9.“两直线平行内错角相等”的逆命题是 命题.(填“真”或“假”)
10.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
11.已知△ABC中,AB=AC=4,∠A=60度,则△ABC的周长为 .
12.如图,在边长为1的正方形网格中,两格点A,B之间的距离为d等于 .
13.如图,点E在?ABCD的边BC的延长线上,若∠DCE=60°,则∠A= °.
(13题) (15题) (16题)
14.△ABC中,三边之比为3:4:5,且最长边为10cm,则△ABC周长为 cm.
15.如图,在△ABC中,∠ABC=90°,分别以△ABC的三边为边向外作正方形,其中两个正方形的面积分别为100,76.则字母a代表的正方形的面积是 .
16.如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E= .
三.解答题(共8小题)
17.解方程
(1); (2).
18.如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
19.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=
(1)求AC、CE的长;
(2)求证:∠ACE=90°.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
21.如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
22.图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
23.如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系(不需证明).
24.我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,和4,则此三角形 常态三角形(填“是”或“不是”);
(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为 (请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,AD=DB=DC,若△BCD是常态三角形,求△ABC的面积.
数学试题
一.选择题(共8小题)
1.下列算式中,正确的是( )
A.=±5 B.±=3 C.=﹣2 D.=﹣1
2.a12可以写成( )
A.a6+a6 B.a2?a6 C.a6?a6 D.a12÷a
3.计算的结果为( )
A.10 B.5 C.3 D.2
4.如图,△ABC中,∠B=90°,BC=3,AC=4,则AB的长度为( )
A.2 B. C.2 D.5
5.用反证法证明“a<1”,应先假设( )
A.a≥1 B.a>1 C.a=1 D.a≠1
6.在△ABC中,AB=AC,∠B=70°,则∠A的度数是( )
A.40° B.55° C.65° D.60°
7.已知:∠AOB.求作:一个角,使它等于∠AOB.步骤如下:如图,
(1)作射线O'A'
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.则∠A'O'B'就是所求作的角.
请回答:该作图的依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,△ABC中,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,若∠BAC=70°,则∠EAN的度数为( )
A.35° B.40° C.50° D.55°
二.填空题(共8小题)
9.“两直线平行内错角相等”的逆命题是 命题.(填“真”或“假”)
10.若一个三角形的三边长分别为5、12、13,则此三角形的面积为 .
11.已知△ABC中,AB=AC=4,∠A=60度,则△ABC的周长为 .
12.如图,在边长为1的正方形网格中,两格点A,B之间的距离为d等于 .
13.如图,点E在?ABCD的边BC的延长线上,若∠DCE=60°,则∠A= °.
(13题) (15题) (16题)
14.△ABC中,三边之比为3:4:5,且最长边为10cm,则△ABC周长为 cm.
15.如图,在△ABC中,∠ABC=90°,分别以△ABC的三边为边向外作正方形,其中两个正方形的面积分别为100,76.则字母a代表的正方形的面积是 .
16.如图所示,BE⊥AC于点D,且AB=CB,BD=ED,若∠ABC=54°,则∠E= .
三.解答题(共8小题)
17.解方程
(1); (2).
18.如图,△ABC中,D为BC边上的一点,AD=AC,以线段AD为边作△ADE,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
19.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=3,BC=2,CD=6,DE=4,AE=
(1)求AC、CE的长;
(2)求证:∠ACE=90°.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
21.如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
22.图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
23.如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
(1)如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
(2)如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系(不需证明).
24.我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
(1)若△ABC三边长分别是2,和4,则此三角形 常态三角形(填“是”或“不是”);
(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为 (请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,AD=DB=DC,若△BCD是常态三角形,求△ABC的面积.
同课章节目录
