青岛版2020-2021学年度上学期九年级期中模拟数学卷(含答案)
文档属性
| 名称 | 青岛版2020-2021学年度上学期九年级期中模拟数学卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 420.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 09:44:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年度第一学期期中模拟卷
九年级数学(时间120分钟,满分120分)
一、单选题(共12题;共36分)
1.如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值(
??
)
A.?扩大为原来的两倍?????????????????????B.?缩小为原来的
?????????????????????C.?不变?????????????????????D.?不能确定
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为(??
)
A.??????????????????
????B.???????????????????
???C.??????????????????
??????D.?
3.下列四个命题中,正确的个数是(
??)
①经过三点一定可以画圆;②任意一个三角形一定有一个外接圆;③三角形的内心是三角形三条角平分线的交点;
④三角形的外心到三角形三个顶点的距离都相等;⑤三角形的外心一定在三角形的外部.
A.?4个????????????????????
?B.?3个??????????????????
??C.?2个?????????????????????
?D.?1个
4.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(?
?
)
A.?(2,4)?????????????
B.?(-1,-2)??????????
????C.?(-2,-4)???????????
???D.?(-2,-1)
5.如图,⊙O的直径AB=12,CD是⊙O的
弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为(?
?
)
A.??????????????????????
B.?????????????
??
????C.??????????????????
??D.?
6.如图,在坡度为
的山坡上种树,要求相邻两棵树的水平距离是6m,则斜坡上相邻两棵树的坡面距离是(?
)
A.?3m???????????????????????
?B.?3
m????????
??
C.?12m????????????
?????
D.?6m
4题图
5题图
6题图
7.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是(??
)
A.?15
海里??????????????????B.?30海里??????????????????C.?45海里?????????????????D.?30
海里
8.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是(
??
)
A.??????????????
?????????B.?6????????????????????????C.??????????????????????
???D.?7
8题图
9题图
10题图
9.如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=GE;?
②△AGE≌△ECF;
③∠FCD=45°;?
④△GBE∽△ECH,其中,正确的结论有(
)
A.?1个?????????????????
?
????B.?2个???????????
??????
????C.?3个???????????????????
?????D.?4个
10.如图,△ABC是等腰三角形,AB=AC=3,BC=1.
点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为(??
)
A.??????????????????????????B.???????????????????????????C.??????????????
????????D.?1
11.如图,正方形
的边长为1,点
是
边上的一点,将
沿着
折叠得
.若
,
恰好都与正方形
的中心
为圆心的
相切,则折痕
的长为(?
?
)
A.????????????????????
?
B.???????????????
??
?C.??????????????????????
?D.?
11题图
12题图
12.如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
的值为(??
)
A.????????????????????????????
?B.????????????????????
??C.??????????????????????
?????D.?1
二、填空题(共6题;共18分)
13.计算:
+(
)﹣2﹣3tan60°+(π
)0=________.
14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门________?步而见木.
15.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、
(0,-1),则△ABC外接圆的圆心坐标为________.
15题图
16题图
17题图
16.如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为________.
17.如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是________cm.
18.如图,
,在
上截取
.过点
作
,交
于点
,以点
为圆心,
为半径画弧,交
于点
;过点
作
,交
于点
,以点
为圆心,
为半径画弧,交
于点
;按此规律,所得线段
的长等于________.
三、作图题(共1题;共8分)
19.如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(﹣2,3),将点O,A,B,C的横坐标、纵坐标都乘以﹣2.
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心
及与原图形的相似比.
四、解答题(共6题;共58分)
20.如图,在?ABCD中,AB=4,AD=9,点E是AD上的一点,AE=2DE
,
延长BE交CD的延长线于F
,
求FD的长.
21.如图,
为
的直角边
上一点,以
为半径的
与斜边
相切于点
,交
于点
.已知
,
.
(1)求
的长;
(2)求图中阴影部分的面积.
22.如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.(参考数据:sin27°≈,
cos27°≈,
tan27°≈,
sin53°≈,
cos53°≈,
tan53°≈)
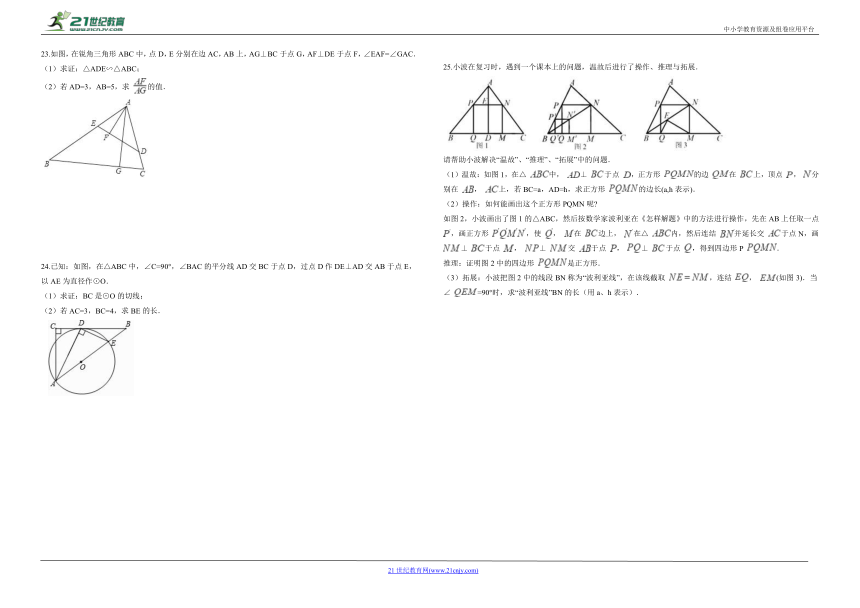
23.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
的值.
24.已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
25.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)温故:如图1,在△
中,
⊥
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若?BC=a,AD=h,求正方形
的边长(a,h表示).
(2)操作:如何能画出这个正方形PQMN呢?
如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点
,画正方形
,使
,
在
边上,
在△
内,然后连结
并延长交
于点N,画
⊥
于点
,
⊥
交
于点
,
⊥
于点
,得到四边形P
.
推理:证明图2中的四边形
是正方形.
拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取
,连结
,
(如图3).当∠
=90°时,求“波利亚线”BN的长(用a、h表示).
2020-2021学年度第一学期期中模拟卷
九年级数学答案解析部分
一、单选题
1.【答案】C
【考点】锐角三角函数的增减性
2.【答案】
A
【考点】锐角三角函数的定义
3.【答案】
B
【考点】圆的认识,三角形的外接圆与外心,三角形的内切圆与内心
4.【答案】
C
【考点】位似变换
5.【答案】
A
【考点】垂径定理,垂径定理的应用
6.【答案】
B
【考点】解直角三角形的应用﹣坡度坡角问题
7.【答案】
B
【考点】解直角三角形的应用﹣方向角问题
8.【答案】
B
【考点】全等三角形的判定与性质,四边形的性质,相似三角形的判定与性质
9.【答案】
C
【考点】解直角三角形
10.【答案】
B
【考点】平行线分线段成比例
11.
【答案】
B
【考点】圆的综合题
12.【答案】
C
【考点】全等三角形的判定与性质,四边形的性质,相似三角形的判定与性质
二、填空题
13.【答案】
10
【考点】实数的运算,特殊角的三角函数值
14.【答案】315
【考点】相似三角形的应用
15.【答案】(2,1)
【考点】垂径定理的应用
16.【答案】
【考点】勾股定理,圆周角定理,相似三角形的判定与性质
17.【答案】
8
【考点】勾股定理,矩形的性质,翻折变换(折叠问题),相似三角形的判定与性质
18.【答案】
【考点】等边三角形的判定与性质,解直角三角形,探索图形规律
三、作图题
19.【答案】解:(1)如图所示,四边形OA′B′C′即为所求四边形;
(2)∵将点O,A,B,C的横坐标、纵坐标都乘以﹣2可得出四边形OA′B′C′,
∴各对应边的比为2,对应点的连线都过原点,
∴得到的四边形与四边形OABC位似,位似中心是O(0,0),与原图形的相似比为2.
【考点】作图-位似变换
【解析】【分析】(1)将点O,A,B,C的横坐标、纵坐标都乘以﹣2得O(0,0),A′(﹣6,0),B′(﹣8,﹣8),C′(4,﹣6),顺次连接各点即可;
(2)根据位似图形的定义可知得到的四边形与四边形OABC位似,根据图形可得出位似中心及位似比.
四、解答题
20.【答案】
∵AD=9,AE=2DE,
∴AE=6,DE=3,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴△ABE∽△DFE,
∴
,
∴
,
解得:DF=2.
【考点】平行四边形的性质,相似三角形的判定与性质
【解析】【分析】求出AE和DE,根据平行四边形的性质得出AB∥CD,根据相似三角形的判定得出△ABE∽△DFE,根据相似得出比例式,代入求出DF即可.
21.【答案】
(1)解:在Rt△ABC中,AB===2
?.
∵BC⊥OC
∴BC是⊙O的切线
又∵AB是⊙O的切线
∴BD=BC=
∴AD=AB-BD=
(2)解:在Rt△ABC中,sinA=
?==.
∴∠A=30°.
∵AB切⊙O于点D.
∴OD⊥AB.
∴∠AOD=90°-∠A=60°.
∵
?=tanA=tan30°.
∴
?=.
∴OD=1.
S阴影==.
【考点】勾股定理,切线的性质,扇形面积的计算,解直角三角形
【解析】【分析】(1)在Rt△ABC中,利用勾股定理求出AB的长,然后根据切线的判定证出BC为切线,然后可根据切线长定理可求解.
(2)在Rt△ABC中,根据∠A的正弦求出∠A度数,然后根据切线的性质求出OD的长,和扇形圆心角的度数,再根据扇形的面积公式可求解.
22.【答案】
解:如图,根据题意可得,在△ABC中,AB=99海里,∠ABC=53°,∠BAC=27°,
过点C作CD⊥AB,垂足为点D.
设BD=x海里,则AD=(99﹣x)海里,
在Rt△BCD中,tan53°=,
则tan27°=,
CD=x?tan53°≈x(海里).
在Rt△ACD中,则CD=AD?tan27°≈(99﹣x),
则x=(99﹣x),
解得,x=27,
即BD=27.
在Rt△BCD中,cos53°=,
则BC===45,
45÷2=22.5(海里/时),
则该可疑船只的航行速度约为22.5海里/时.
【考点】解直角三角形的应用﹣方向角问题
【解析】【分析】先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(99﹣x)海里,在Rt△BCD中,根据tan53°=,
求出CD,再根据x=(99﹣x),求出BD,在Rt△BCD中,根据cos53°=?,求出BC,从而得出答案.
23.【答案】
(1)证明:∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°,
∵∠EAF=∠GAC,
∴∠AED=∠ACB,
∵∠EAD=∠BAC,
∴△ADE∽△ABC
(2)解:由(1)可知:△ADE∽△ABC,
∴
=
由(1)可知:∠AFE=∠AGC=90°,
∴∠EAF=∠GAC,
∴△EAF∽△CAG,
∴
,
∴
=
【考点】相似三角形的判定与性质
【解析】【分析】(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)△ADE∽△ABC,
,又易证△EAF∽△CAG,所以
,从而可知
.
24.【答案】
(1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=
AE,
∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠ADO=∠CAD,
∴AC∥DO.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线
(2)解:∵在Rt△ACB中,AC=3,BC=4,
∴AB=5.
设OD=r,则BO=5﹣r.
∵OD∥AC,
∴△BDO∽△BCA,
∴
=
,即
=
,
解得:r=
,
∴BE=AB﹣AE=5﹣
=
【考点】切线的判定与性质,相似三角形的判定与性质
【解析】【分析】(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出
=
,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
25.【答案】
(1)解:由正方形PQMN得PN∥BC,
∴△APN∽△ABC.
∴
,即.
?
解得PN=
(2)证明:推理:由画法可得∠QMN=∠PNM=∠PQM=∠Q'M'N'=90°,
∴四边形PQMN为矩形,MN∥M'N'.
∴△BN'M'∽△BNM.
∴
同理可得
∴
:M'N'=P'N',∴MN=PN
∴四边形PQMN为正方形。
(3)解:过N作NR⊥EM于点R,
∵NE=NM,
∴∠NEM=∠NME,
∴ER=RM=
?EM,
又∵∠EQM+∠EMQ=∠EMQ+∠EMN=90°,
∴∠EQM=∠EMN,
又∠QEM=∠NRM=90°,NM=QM,
∴△EQM≌△RMN(AAS)
∴EQ=RM,
∴EQ=
?EM,
∵∠QEM=90°,
∴∠BEQ+∠NEM=90°,
∴BEQ=∠EMB,
又∵∠EBM=∠QBE,
∴△BEQ∽△BME,
∴
?,
设BQ=x,则BE=2x,BM=4x,
∴QM=BM-BQ=3x=MN=NE,
∴BN=BE+NE=5x,
∴BN=
?NM=
?
【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
【解析】【分析】(1)温故:利用正方形的性质易证PN∥BC,就可证得△PAN∽△ABC,再利用相似三角形的性质,得出对应边成比例,建立关于PN的方程,解方程求出PN的长。
(2)推理:根据画法易证四边形PQMN是矩形,可得到MN∥M'N',易证△BMN和△BM'N',再利用相似三角形的性质,得出对应边成比例,同理可证△P'BN'∽△PBN,得出对应边成比例,利用中间比及M'N'=P'N',可证MN=PN,然后利用一组邻边相等的矩形是正方形,可证得结论。
(3)
拓展:
过N作NR⊥EM于点R,
根据已知条件去证明
△EQM≌△RMN,利用全等三角形的性质,可证得
EQ=RM,即可得到
EQ=
?EM
,再证明
△BEQ∽△BME,利用相似三角形的性质,得出对应边成比例,设BQ=x,用含x的代数式分别表示出BE、BM、QM、BN,
然后根据
BN=
?NM,就可求出“波利亚线”BN的长、
21世纪教育网(www.21cnjy.com)
2020-2021学年度第一学期期中模拟卷
九年级数学(时间120分钟,满分120分)
一、单选题(共12题;共36分)
1.如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值(
??
)
A.?扩大为原来的两倍?????????????????????B.?缩小为原来的
?????????????????????C.?不变?????????????????????D.?不能确定
2.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cosB的值为(??
)
A.??????????????????
????B.???????????????????
???C.??????????????????
??????D.?
3.下列四个命题中,正确的个数是(
??)
①经过三点一定可以画圆;②任意一个三角形一定有一个外接圆;③三角形的内心是三角形三条角平分线的交点;
④三角形的外心到三角形三个顶点的距离都相等;⑤三角形的外心一定在三角形的外部.
A.?4个????????????????????
?B.?3个??????????????????
??C.?2个?????????????????????
?D.?1个
4.如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是(?
?
)
A.?(2,4)?????????????
B.?(-1,-2)??????????
????C.?(-2,-4)???????????
???D.?(-2,-1)
5.如图,⊙O的直径AB=12,CD是⊙O的
弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为(?
?
)
A.??????????????????????
B.?????????????
??
????C.??????????????????
??D.?
6.如图,在坡度为
的山坡上种树,要求相邻两棵树的水平距离是6m,则斜坡上相邻两棵树的坡面距离是(?
)
A.?3m???????????????????????
?B.?3
m????????
??
C.?12m????????????
?????
D.?6m
4题图
5题图
6题图
7.如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是(??
)
A.?15
海里??????????????????B.?30海里??????????????????C.?45海里?????????????????D.?30
海里
8.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是(
??
)
A.??????????????
?????????B.?6????????????????????????C.??????????????????????
???D.?7
8题图
9题图
10题图
9.如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=GE;?
②△AGE≌△ECF;
③∠FCD=45°;?
④△GBE∽△ECH,其中,正确的结论有(
)
A.?1个?????????????????
?
????B.?2个???????????
??????
????C.?3个???????????????????
?????D.?4个
10.如图,△ABC是等腰三角形,AB=AC=3,BC=1.
点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为(??
)
A.??????????????????????????B.???????????????????????????C.??????????????
????????D.?1
11.如图,正方形
的边长为1,点
是
边上的一点,将
沿着
折叠得
.若
,
恰好都与正方形
的中心
为圆心的
相切,则折痕
的长为(?
?
)
A.????????????????????
?
B.???????????????
??
?C.??????????????????????
?D.?
11题图
12题图
12.如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
的值为(??
)
A.????????????????????????????
?B.????????????????????
??C.??????????????????????
?????D.?1
二、填空题(共6题;共18分)
13.计算:
+(
)﹣2﹣3tan60°+(π
)0=________.
14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门________?步而见木.
15.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、
(0,-1),则△ABC外接圆的圆心坐标为________.
15题图
16题图
17题图
16.如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为________.
17.如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是________cm.
18.如图,
,在
上截取
.过点
作
,交
于点
,以点
为圆心,
为半径画弧,交
于点
;过点
作
,交
于点
,以点
为圆心,
为半径画弧,交
于点
;按此规律,所得线段
的长等于________.
三、作图题(共1题;共8分)
19.如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(﹣2,3),将点O,A,B,C的横坐标、纵坐标都乘以﹣2.
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心
及与原图形的相似比.
四、解答题(共6题;共58分)
20.如图,在?ABCD中,AB=4,AD=9,点E是AD上的一点,AE=2DE
,
延长BE交CD的延长线于F
,
求FD的长.
21.如图,
为
的直角边
上一点,以
为半径的
与斜边
相切于点
,交
于点
.已知
,
.
(1)求
的长;
(2)求图中阴影部分的面积.
22.如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.(参考数据:sin27°≈,
cos27°≈,
tan27°≈,
sin53°≈,
cos53°≈,
tan53°≈)
23.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
的值.
24.已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:BC是⊙O的切线;
(2)若AC=3,BC=4,求BE的长.
25.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)温故:如图1,在△
中,
⊥
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若?BC=a,AD=h,求正方形
的边长(a,h表示).
(2)操作:如何能画出这个正方形PQMN呢?
如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点
,画正方形
,使
,
在
边上,
在△
内,然后连结
并延长交
于点N,画
⊥
于点
,
⊥
交
于点
,
⊥
于点
,得到四边形P
.
推理:证明图2中的四边形
是正方形.
拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取
,连结
,
(如图3).当∠
=90°时,求“波利亚线”BN的长(用a、h表示).
2020-2021学年度第一学期期中模拟卷
九年级数学答案解析部分
一、单选题
1.【答案】C
【考点】锐角三角函数的增减性
2.【答案】
A
【考点】锐角三角函数的定义
3.【答案】
B
【考点】圆的认识,三角形的外接圆与外心,三角形的内切圆与内心
4.【答案】
C
【考点】位似变换
5.【答案】
A
【考点】垂径定理,垂径定理的应用
6.【答案】
B
【考点】解直角三角形的应用﹣坡度坡角问题
7.【答案】
B
【考点】解直角三角形的应用﹣方向角问题
8.【答案】
B
【考点】全等三角形的判定与性质,四边形的性质,相似三角形的判定与性质
9.【答案】
C
【考点】解直角三角形
10.【答案】
B
【考点】平行线分线段成比例
11.
【答案】
B
【考点】圆的综合题
12.【答案】
C
【考点】全等三角形的判定与性质,四边形的性质,相似三角形的判定与性质
二、填空题
13.【答案】
10
【考点】实数的运算,特殊角的三角函数值
14.【答案】315
【考点】相似三角形的应用
15.【答案】(2,1)
【考点】垂径定理的应用
16.【答案】
【考点】勾股定理,圆周角定理,相似三角形的判定与性质
17.【答案】
8
【考点】勾股定理,矩形的性质,翻折变换(折叠问题),相似三角形的判定与性质
18.【答案】
【考点】等边三角形的判定与性质,解直角三角形,探索图形规律
三、作图题
19.【答案】解:(1)如图所示,四边形OA′B′C′即为所求四边形;
(2)∵将点O,A,B,C的横坐标、纵坐标都乘以﹣2可得出四边形OA′B′C′,
∴各对应边的比为2,对应点的连线都过原点,
∴得到的四边形与四边形OABC位似,位似中心是O(0,0),与原图形的相似比为2.
【考点】作图-位似变换
【解析】【分析】(1)将点O,A,B,C的横坐标、纵坐标都乘以﹣2得O(0,0),A′(﹣6,0),B′(﹣8,﹣8),C′(4,﹣6),顺次连接各点即可;
(2)根据位似图形的定义可知得到的四边形与四边形OABC位似,根据图形可得出位似中心及位似比.
四、解答题
20.【答案】
∵AD=9,AE=2DE,
∴AE=6,DE=3,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴△ABE∽△DFE,
∴
,
∴
,
解得:DF=2.
【考点】平行四边形的性质,相似三角形的判定与性质
【解析】【分析】求出AE和DE,根据平行四边形的性质得出AB∥CD,根据相似三角形的判定得出△ABE∽△DFE,根据相似得出比例式,代入求出DF即可.
21.【答案】
(1)解:在Rt△ABC中,AB===2
?.
∵BC⊥OC
∴BC是⊙O的切线
又∵AB是⊙O的切线
∴BD=BC=
∴AD=AB-BD=
(2)解:在Rt△ABC中,sinA=
?==.
∴∠A=30°.
∵AB切⊙O于点D.
∴OD⊥AB.
∴∠AOD=90°-∠A=60°.
∵
?=tanA=tan30°.
∴
?=.
∴OD=1.
S阴影==.
【考点】勾股定理,切线的性质,扇形面积的计算,解直角三角形
【解析】【分析】(1)在Rt△ABC中,利用勾股定理求出AB的长,然后根据切线的判定证出BC为切线,然后可根据切线长定理可求解.
(2)在Rt△ABC中,根据∠A的正弦求出∠A度数,然后根据切线的性质求出OD的长,和扇形圆心角的度数,再根据扇形的面积公式可求解.
22.【答案】
解:如图,根据题意可得,在△ABC中,AB=99海里,∠ABC=53°,∠BAC=27°,
过点C作CD⊥AB,垂足为点D.
设BD=x海里,则AD=(99﹣x)海里,
在Rt△BCD中,tan53°=,
则tan27°=,
CD=x?tan53°≈x(海里).
在Rt△ACD中,则CD=AD?tan27°≈(99﹣x),
则x=(99﹣x),
解得,x=27,
即BD=27.
在Rt△BCD中,cos53°=,
则BC===45,
45÷2=22.5(海里/时),
则该可疑船只的航行速度约为22.5海里/时.
【考点】解直角三角形的应用﹣方向角问题
【解析】【分析】先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(99﹣x)海里,在Rt△BCD中,根据tan53°=,
求出CD,再根据x=(99﹣x),求出BD,在Rt△BCD中,根据cos53°=?,求出BC,从而得出答案.
23.【答案】
(1)证明:∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°,
∵∠EAF=∠GAC,
∴∠AED=∠ACB,
∵∠EAD=∠BAC,
∴△ADE∽△ABC
(2)解:由(1)可知:△ADE∽△ABC,
∴
=
由(1)可知:∠AFE=∠AGC=90°,
∴∠EAF=∠GAC,
∴△EAF∽△CAG,
∴
,
∴
=
【考点】相似三角形的判定与性质
【解析】【分析】(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)△ADE∽△ABC,
,又易证△EAF∽△CAG,所以
,从而可知
.
24.【答案】
(1)证明:连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=
AE,
∴点D在⊙O上,且∠DAO=∠ADO.
又∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠ADO=∠CAD,
∴AC∥DO.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵OD为半径,
∴BC是⊙O的切线
(2)解:∵在Rt△ACB中,AC=3,BC=4,
∴AB=5.
设OD=r,则BO=5﹣r.
∵OD∥AC,
∴△BDO∽△BCA,
∴
=
,即
=
,
解得:r=
,
∴BE=AB﹣AE=5﹣
=
【考点】切线的判定与性质,相似三角形的判定与性质
【解析】【分析】(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;(2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出
=
,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度.
25.【答案】
(1)解:由正方形PQMN得PN∥BC,
∴△APN∽△ABC.
∴
,即.
?
解得PN=
(2)证明:推理:由画法可得∠QMN=∠PNM=∠PQM=∠Q'M'N'=90°,
∴四边形PQMN为矩形,MN∥M'N'.
∴△BN'M'∽△BNM.
∴
同理可得
∴
:M'N'=P'N',∴MN=PN
∴四边形PQMN为正方形。
(3)解:过N作NR⊥EM于点R,
∵NE=NM,
∴∠NEM=∠NME,
∴ER=RM=
?EM,
又∵∠EQM+∠EMQ=∠EMQ+∠EMN=90°,
∴∠EQM=∠EMN,
又∠QEM=∠NRM=90°,NM=QM,
∴△EQM≌△RMN(AAS)
∴EQ=RM,
∴EQ=
?EM,
∵∠QEM=90°,
∴∠BEQ+∠NEM=90°,
∴BEQ=∠EMB,
又∵∠EBM=∠QBE,
∴△BEQ∽△BME,
∴
?,
设BQ=x,则BE=2x,BM=4x,
∴QM=BM-BQ=3x=MN=NE,
∴BN=BE+NE=5x,
∴BN=
?NM=
?
【考点】全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
【解析】【分析】(1)温故:利用正方形的性质易证PN∥BC,就可证得△PAN∽△ABC,再利用相似三角形的性质,得出对应边成比例,建立关于PN的方程,解方程求出PN的长。
(2)推理:根据画法易证四边形PQMN是矩形,可得到MN∥M'N',易证△BMN和△BM'N',再利用相似三角形的性质,得出对应边成比例,同理可证△P'BN'∽△PBN,得出对应边成比例,利用中间比及M'N'=P'N',可证MN=PN,然后利用一组邻边相等的矩形是正方形,可证得结论。
(3)
拓展:
过N作NR⊥EM于点R,
根据已知条件去证明
△EQM≌△RMN,利用全等三角形的性质,可证得
EQ=RM,即可得到
EQ=
?EM
,再证明
△BEQ∽△BME,利用相似三角形的性质,得出对应边成比例,设BQ=x,用含x的代数式分别表示出BE、BM、QM、BN,
然后根据
BN=
?NM,就可求出“波利亚线”BN的长、
21世纪教育网(www.21cnjy.com)
同课章节目录
