人教版八年级数学下册四边形最值问题(图片版,附答案)
文档属性
| 名称 | 人教版八年级数学下册四边形最值问题(图片版,附答案) | 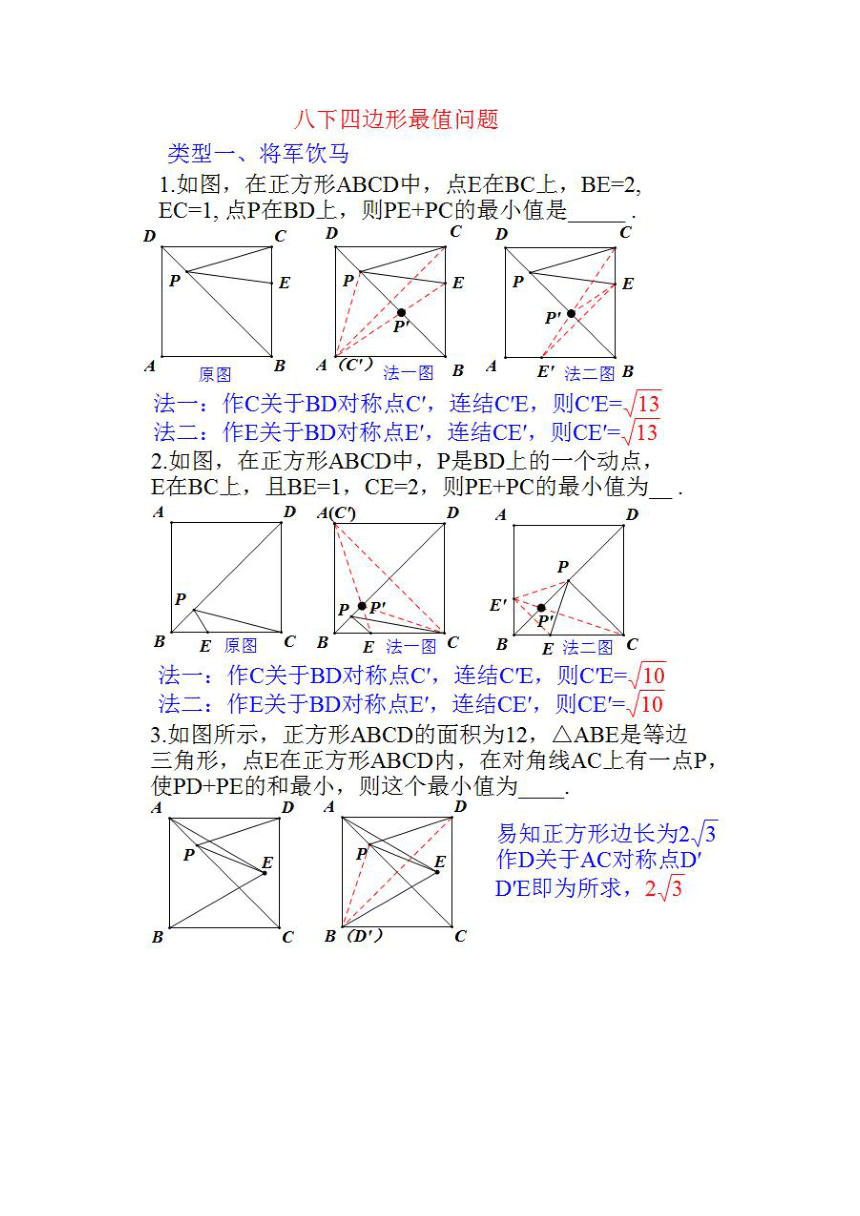 | |
| 格式 | zip | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 17:47:47 | ||
图片预览




文档简介
下四边形最值问题
类
军饮
如图,在正方形ABCD中,点E在BC上,BF
EC=1,点P在BD上,则PE+PC的最小值是
C
E
E
原图
图
法
关于BD对称
连结C
E关于BD对称
连
图,在正方形ABC
P是BD上
动
E在BC上
E=1,CE=2,则PE+PC的最小值为
BE原图
E法一图
E法二图C
关于BD对称点C′,连结CE,则CE
法
E关于BD对称
连结CE',
如图所示,正方形ABCD的面积为
正是等
角形,点E在正方形ABCD内,在对角线AC上
使PD+PE的和最小,则这个最小值为
易知正方形边长为23
作D关于AC对称
E即为所
B
C
四边形最值
类
点到直线距离垂线段最短
在边长为2菱形ABC
abC
I、N分别为
线段BC和BD上两个动点,则MN+CN的最小值是
M
原图
图
图
关于BD对称
易知CM⊥AB取最小值
2.如图,在Rt
C
ac-8,
BC=6
P是AB上的任意一点,作PD⊥AC
PE⊥CB于点E
连接DE,则DE的最小值为
CE原图BCE
C最值图E
连
E,易知CP⊥AB时,CP取最小值4
在△ABC中
6,AC=8,BC=10,P为边BC上一动
P
于E,PF⊥AC于F,M为E
M的最小值为
原图
图
值图
B
易知四边形EPFA为矩形,连结MP
AP,AP⊥BC时
AP最小为48,
最小值为2.4
下四边形最值问题
类型三、平行线
距离为最值
图,菱形ABCD的边长为5,面积为20,P为CD边上
动点(异于C
点M、N分别在
C上
PM+MN的最小值为
原图
易知高h=4,作N关于BD对称
M+MN>h,最小值为4
上左图,菱形ABC
M、N
分别为线段
上的任意一点,
最小值为
G
N
原图
图
图
于BD的对称
易知
线且垂直AB时取最值
最小值时长度等于AG
Ag
下四边形最值问题
类型四、利用三角形
线取最值
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上
当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状
保持不变,其
动过程
到点O的最大距离为
原图
最值图
B
取AB
据三角形三边
M+MD,而当
线时,
M+DM为最大
易知:OM=1,勾股
如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动
当正方形的边长为2时,OD的最大值为
原图
乍图
取AB
连
,根据三角形
知
MD,而
线时,
+DM为最大
易知:OM=1,勾股求得DM
如图,正方形ABCD的边长为4,点P为边AD上一动点,AE⊥BP,
垂足为E,连DE,求DE的最小值
动时,∠AEB=90°不变
取Rt△ABE
点O,连
E
E
易知当O、E
共线时DE取最小值
B最值图C
OE=2,勾股
B原图C
类
军饮
如图,在正方形ABCD中,点E在BC上,BF
EC=1,点P在BD上,则PE+PC的最小值是
C
E
E
原图
图
法
关于BD对称
连结C
E关于BD对称
连
图,在正方形ABC
P是BD上
动
E在BC上
E=1,CE=2,则PE+PC的最小值为
BE原图
E法一图
E法二图C
关于BD对称点C′,连结CE,则CE
法
E关于BD对称
连结CE',
如图所示,正方形ABCD的面积为
正是等
角形,点E在正方形ABCD内,在对角线AC上
使PD+PE的和最小,则这个最小值为
易知正方形边长为23
作D关于AC对称
E即为所
B
C
四边形最值
类
点到直线距离垂线段最短
在边长为2菱形ABC
abC
I、N分别为
线段BC和BD上两个动点,则MN+CN的最小值是
M
原图
图
图
关于BD对称
易知CM⊥AB取最小值
2.如图,在Rt
C
ac-8,
BC=6
P是AB上的任意一点,作PD⊥AC
PE⊥CB于点E
连接DE,则DE的最小值为
CE原图BCE
C最值图E
连
E,易知CP⊥AB时,CP取最小值4
在△ABC中
6,AC=8,BC=10,P为边BC上一动
P
于E,PF⊥AC于F,M为E
M的最小值为
原图
图
值图
B
易知四边形EPFA为矩形,连结MP
AP,AP⊥BC时
AP最小为48,
最小值为2.4
下四边形最值问题
类型三、平行线
距离为最值
图,菱形ABCD的边长为5,面积为20,P为CD边上
动点(异于C
点M、N分别在
C上
PM+MN的最小值为
原图
易知高h=4,作N关于BD对称
M+MN>h,最小值为4
上左图,菱形ABC
M、N
分别为线段
上的任意一点,
最小值为
G
N
原图
图
图
于BD的对称
易知
线且垂直AB时取最值
最小值时长度等于AG
Ag
下四边形最值问题
类型四、利用三角形
线取最值
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上
当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状
保持不变,其
动过程
到点O的最大距离为
原图
最值图
B
取AB
据三角形三边
M+MD,而当
线时,
M+DM为最大
易知:OM=1,勾股
如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动
当正方形的边长为2时,OD的最大值为
原图
乍图
取AB
连
,根据三角形
知
MD,而
线时,
+DM为最大
易知:OM=1,勾股求得DM
如图,正方形ABCD的边长为4,点P为边AD上一动点,AE⊥BP,
垂足为E,连DE,求DE的最小值
动时,∠AEB=90°不变
取Rt△ABE
点O,连
E
E
易知当O、E
共线时DE取最小值
B最值图C
OE=2,勾股
B原图C
