人教版八年级上数学轴对称——最短路径问题(Word版,无答案)
文档属性
| 名称 | 人教版八年级上数学轴对称——最短路径问题(Word版,无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 00:00:00 | ||
图片预览


文档简介
第11讲:轴对称
【问题概述】初中数学最值问题是每年中考必出题,更是图论研究中的一个经典算法问题,
旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。
【问题原型】“将军饮马”,“造桥选址”,“费马点”.
【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.
【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.
【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.
一.【十二个基本问题】
【问题
1】
作法
作图
原理
在直线
l
上求一点
P,使PA+PB
值最小。
连
AB,与
l
交点即为
P.
两点之间线段最短.PA+PB
最小值为
AB.
【问题
2】
作法
作图
原理
在直线
l
上求一点
P,使PA+PB
值最小.
作
B
关于
l
的对称点
B'连
A
B',与
l
交点即为
P.
两点之间线段最短.PA+PB
最小值为A
B'.
【问题
3】“将军饮马”
作法
作图
原理
在直线
l1
、
l2
上分别求点M、N,使△PMN
的周长最小.
分别作点
P
关于两直线的对称点
P'和
P',连
P'P',与两直线交点即为
M,N.
两点之间线段最短.PM+MN+PN
的最小值为线段
P'P''的长。
【问题
4】
作法
作图
原理
在直线
l1
、
l2
上分别求点M
、N
,使四边形
PQMN的周长最小。
分别作点
Q
、P
关于直线l1
、
l2
的对称点
Q'和
P'连
Q'P',与两直线交点即为
M,N.
两点之间线段最短四边形
PQMN
周长的最小值为线段
Q'P'的长。
【问题
5】“造桥选址”
作法
作图
原理
直线
m
∥
n
,在
m
、
n,上分别求点
M、N,使
MN⊥m
,且
AM+MN+BN的值最小。
将点
A
向下平移
MN
的长度单位得
A',连
A'B,交
n于点
N,过
N
作
NM⊥
m
于M
.
两点之间线段最短.AM+MN+BN
的最小值为A'B+MN.
【问题
6】
作法
作图
原理
在直线
l
上求两点
M、N(M在左),使
MN
?
a
,并使AM+MN+NB
的值最小
.
将点
A
向右平移
a
个长度单位得
A',作
A'关于
l的对称点
A'',连
A''B,交直线
l
于点
N,将
N
点向左平移
a
个单位得
M.
两点之间线段最短.AM+MN+BN
的最小值为A''B+MN.
【问题
7】
作法
作图
原理
在
l1
上求点
A,在
l2
上求点
B,使
PA+AB
值最小.
作点
P
关于
l1
的对称点P',作
P'B⊥
l2于B,交l1
于
A.
点到直线,垂线段最短PA+AB
的值最小为P'B
【问题
8】
作法
作图
原理
A
为
l1
上一定点,B
为
l2
上;A
为
l1
上一定点,B
为
l2上一定点,在
l2
上求点M在l1上求点N
,
使AM+MN+NB
的值最小.
作点
A
关于
l2
的对称点A',作点
B
关于
l1
的对称点
B',连
A'B'交l2
于M,交
l1
于
N
.
两点之间线段最短AM+MN+NB
的最小值为线段
A'B'的长.
【问题
9】
作法
作图
原理
在直线
l
上求一点
P,使的值最小
.
连
AB,作
AB
的中垂线与直线
l
的交点即为
P.
垂直平分上的点到线段两端点的距离相等.=0
.
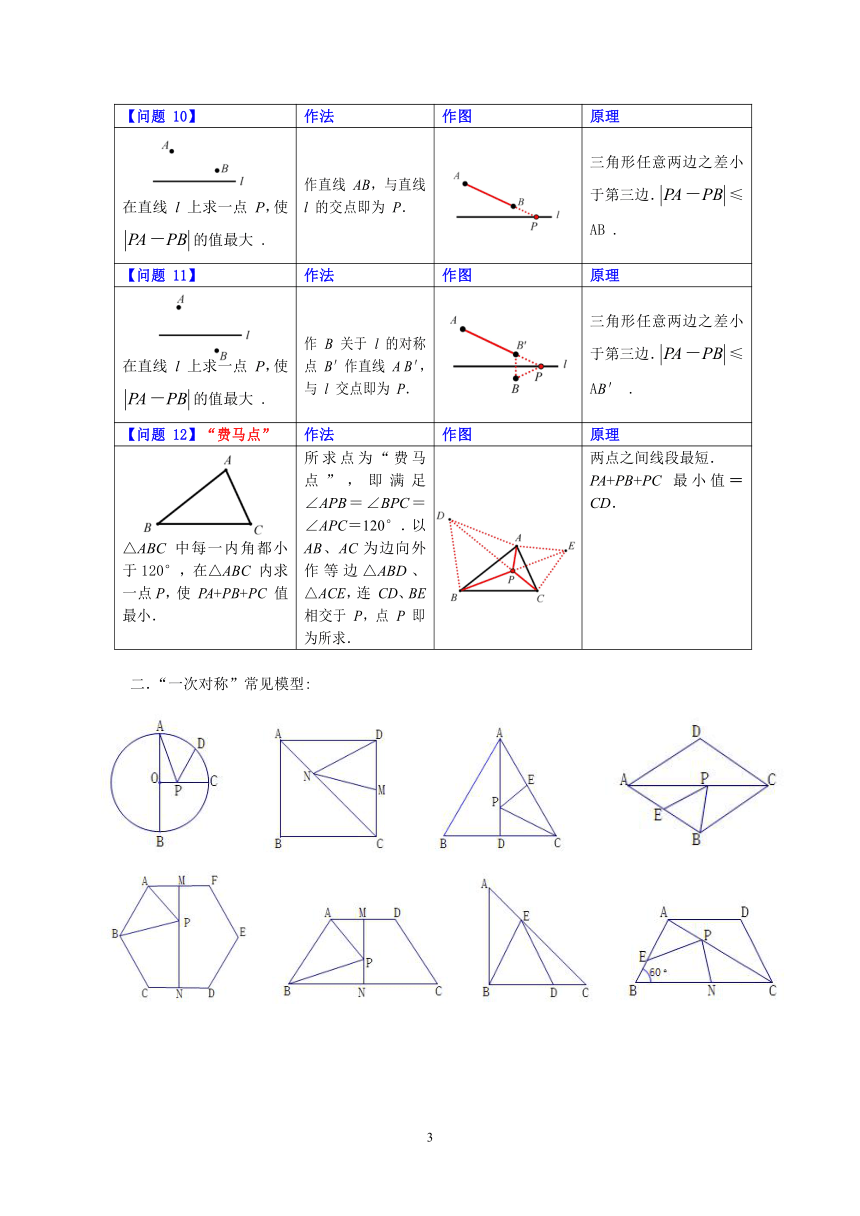
【问题
10】
作法
作图
原理
在直线
l
上求一点
P,使的值最大
.
作直线
AB,与直线
l
的交点即为
P.
三角形任意两边之差小于第三边.≤AB
.
【问题
11】
作法
作图
原理
在直线
l
上求一点
P,使的值最大
.
作
B
关于
l
的对称点
B'作直线
A
B',与
l
交点即为
P.
三角形任意两边之差小于第三边.≤AB'
.
【问题
12】“费马点”
作法
作图
原理
△ABC
中每一内角都小于120°,在△ABC
内求一点P,使
PA+PB+PC
值最小.
所求点为“费马点”,即满足∠APB=∠BPC=∠APC=120°.以
AB、AC为边向外作等边△ABD、△ACE,连
CD、BE
相交于
P,点
P
即为所求.
两点之间线段最短.PA+PB+PC
最小值=CD.
二.“一次对称”常见模型:
【精品练习】
如图所示,正方形
ABCD
的面积为
12,△ABE
是等边三角形,点
E
在正方形
ABCD
内,在对角线
AC
上有一点
P,使
PD+PE
的和最小,则这个最小值为(
)
A.2
B.
2
C.3
D.
如图,在边长为
2
的菱形
ABCD
中,∠ABC=60°,若将△ACD
绕点
A
旋转,当
AC′、AD′分别与
BC、CD交于点
E、F,则△CEF
的周长的最小值为(
)
A.2
B.2
C.2+
D.
4
3.四边形
ABCD
中,∠B=∠D=90°,∠C=70°,在
BC、CD
上分别找一点
M、N,使△AMN
的周长最小时,
∠AMN+∠ANM
的度数为(
)
A.120°
B.130°
C.110°
D.140°
4.如图,在锐角△ABC
中,AB=4,∠BAC=45°,∠BAC=45°,∠BAC
的平分线交
BC
于点
D,M、N
分别是
AD
和AB上的动点,则
BM+MN
的最小值是__________。
5.如图,Rt△ABC
中,∠C=90°,∠B=30°,AB=6,点
E
在
AB
边上,点
D
在
BC
边上(不与点
B、C
重合),且
ED=AE,则线段
AE
的取值范围是__________。
6.如图,∠AOB=30°,点
M、N
分别在边
OA、OB
上,且
OM=1,ON=3,点
P、Q
分别在边
OB、OA
上,则
MP+PQ+QN
的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即
Rt△ABC
中,∠C=90°,则有
AC
2
?
BC
2
?
AB
2
)
7.如图,三角形△ABC
中,∠OAB=∠AOB=15°,点
B
在
x
轴的正半轴,坐标为
B(
6,0).OC
平分∠AOB,点
M
在
OC
的延长线上,点
N
为边
OA
上的点,则
MA+MN
的最小值__________。
8.已知
A(2,4)、B(4,2).C
在
y
轴上,D
在
x
轴上,则四边形
ABCD
的周长最小值为__________。
此时
C、D
两点的坐标分别为__________。
9.已知
A(1,1)、B(4,2).(1)P
为
x
轴上一动点,求
PA+PB
的最小值和此时
P
点的坐标;(2)P
为
x
轴上一动点,求
PA
?
PB
的值最大时
P
点的坐标;
(3)CD
为
x
轴上一条动线段,D
在
C
点右边且
CD=1,求当
AC+CD+DB
的最小值和此时
C
点的坐标;
点
C
为∠AOB
内一点.(1)在
OA
求作点
D,OB
上求作点
E,使△CDE
的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE
周长的最小值和此时∠DCE
的度数.
11.(1)如图①,△ABD
和△ACE
均为等边三角形,BE、CE
交于
F,连
AF,求证:AF+BF+CF=CD;(2)在△ABC
中,∠ABC=30°,AB=6,BC=8,∠A,∠C
均小于
120°,求作一点
P,使
PA+PB+PC
的值最小,试求出最小值并说明理由.
12.荆州护城河在
CC'处直角转弯,河宽相等,从
A
处到达
B
处,需经过两座桥
DD'、EE',护城河及两
桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使
A
到
B
点路径最短?
PAGE
【问题概述】初中数学最值问题是每年中考必出题,更是图论研究中的一个经典算法问题,
旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。
【问题原型】“将军饮马”,“造桥选址”,“费马点”.
【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.
【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.
【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.
一.【十二个基本问题】
【问题
1】
作法
作图
原理
在直线
l
上求一点
P,使PA+PB
值最小。
连
AB,与
l
交点即为
P.
两点之间线段最短.PA+PB
最小值为
AB.
【问题
2】
作法
作图
原理
在直线
l
上求一点
P,使PA+PB
值最小.
作
B
关于
l
的对称点
B'连
A
B',与
l
交点即为
P.
两点之间线段最短.PA+PB
最小值为A
B'.
【问题
3】“将军饮马”
作法
作图
原理
在直线
l1
、
l2
上分别求点M、N,使△PMN
的周长最小.
分别作点
P
关于两直线的对称点
P'和
P',连
P'P',与两直线交点即为
M,N.
两点之间线段最短.PM+MN+PN
的最小值为线段
P'P''的长。
【问题
4】
作法
作图
原理
在直线
l1
、
l2
上分别求点M
、N
,使四边形
PQMN的周长最小。
分别作点
Q
、P
关于直线l1
、
l2
的对称点
Q'和
P'连
Q'P',与两直线交点即为
M,N.
两点之间线段最短四边形
PQMN
周长的最小值为线段
Q'P'的长。
【问题
5】“造桥选址”
作法
作图
原理
直线
m
∥
n
,在
m
、
n,上分别求点
M、N,使
MN⊥m
,且
AM+MN+BN的值最小。
将点
A
向下平移
MN
的长度单位得
A',连
A'B,交
n于点
N,过
N
作
NM⊥
m
于M
.
两点之间线段最短.AM+MN+BN
的最小值为A'B+MN.
【问题
6】
作法
作图
原理
在直线
l
上求两点
M、N(M在左),使
MN
?
a
,并使AM+MN+NB
的值最小
.
将点
A
向右平移
a
个长度单位得
A',作
A'关于
l的对称点
A'',连
A''B,交直线
l
于点
N,将
N
点向左平移
a
个单位得
M.
两点之间线段最短.AM+MN+BN
的最小值为A''B+MN.
【问题
7】
作法
作图
原理
在
l1
上求点
A,在
l2
上求点
B,使
PA+AB
值最小.
作点
P
关于
l1
的对称点P',作
P'B⊥
l2于B,交l1
于
A.
点到直线,垂线段最短PA+AB
的值最小为P'B
【问题
8】
作法
作图
原理
A
为
l1
上一定点,B
为
l2
上;A
为
l1
上一定点,B
为
l2上一定点,在
l2
上求点M在l1上求点N
,
使AM+MN+NB
的值最小.
作点
A
关于
l2
的对称点A',作点
B
关于
l1
的对称点
B',连
A'B'交l2
于M,交
l1
于
N
.
两点之间线段最短AM+MN+NB
的最小值为线段
A'B'的长.
【问题
9】
作法
作图
原理
在直线
l
上求一点
P,使的值最小
.
连
AB,作
AB
的中垂线与直线
l
的交点即为
P.
垂直平分上的点到线段两端点的距离相等.=0
.
【问题
10】
作法
作图
原理
在直线
l
上求一点
P,使的值最大
.
作直线
AB,与直线
l
的交点即为
P.
三角形任意两边之差小于第三边.≤AB
.
【问题
11】
作法
作图
原理
在直线
l
上求一点
P,使的值最大
.
作
B
关于
l
的对称点
B'作直线
A
B',与
l
交点即为
P.
三角形任意两边之差小于第三边.≤AB'
.
【问题
12】“费马点”
作法
作图
原理
△ABC
中每一内角都小于120°,在△ABC
内求一点P,使
PA+PB+PC
值最小.
所求点为“费马点”,即满足∠APB=∠BPC=∠APC=120°.以
AB、AC为边向外作等边△ABD、△ACE,连
CD、BE
相交于
P,点
P
即为所求.
两点之间线段最短.PA+PB+PC
最小值=CD.
二.“一次对称”常见模型:
【精品练习】
如图所示,正方形
ABCD
的面积为
12,△ABE
是等边三角形,点
E
在正方形
ABCD
内,在对角线
AC
上有一点
P,使
PD+PE
的和最小,则这个最小值为(
)
A.2
B.
2
C.3
D.
如图,在边长为
2
的菱形
ABCD
中,∠ABC=60°,若将△ACD
绕点
A
旋转,当
AC′、AD′分别与
BC、CD交于点
E、F,则△CEF
的周长的最小值为(
)
A.2
B.2
C.2+
D.
4
3.四边形
ABCD
中,∠B=∠D=90°,∠C=70°,在
BC、CD
上分别找一点
M、N,使△AMN
的周长最小时,
∠AMN+∠ANM
的度数为(
)
A.120°
B.130°
C.110°
D.140°
4.如图,在锐角△ABC
中,AB=4,∠BAC=45°,∠BAC=45°,∠BAC
的平分线交
BC
于点
D,M、N
分别是
AD
和AB上的动点,则
BM+MN
的最小值是__________。
5.如图,Rt△ABC
中,∠C=90°,∠B=30°,AB=6,点
E
在
AB
边上,点
D
在
BC
边上(不与点
B、C
重合),且
ED=AE,则线段
AE
的取值范围是__________。
6.如图,∠AOB=30°,点
M、N
分别在边
OA、OB
上,且
OM=1,ON=3,点
P、Q
分别在边
OB、OA
上,则
MP+PQ+QN
的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即
Rt△ABC
中,∠C=90°,则有
AC
2
?
BC
2
?
AB
2
)
7.如图,三角形△ABC
中,∠OAB=∠AOB=15°,点
B
在
x
轴的正半轴,坐标为
B(
6,0).OC
平分∠AOB,点
M
在
OC
的延长线上,点
N
为边
OA
上的点,则
MA+MN
的最小值__________。
8.已知
A(2,4)、B(4,2).C
在
y
轴上,D
在
x
轴上,则四边形
ABCD
的周长最小值为__________。
此时
C、D
两点的坐标分别为__________。
9.已知
A(1,1)、B(4,2).(1)P
为
x
轴上一动点,求
PA+PB
的最小值和此时
P
点的坐标;(2)P
为
x
轴上一动点,求
PA
?
PB
的值最大时
P
点的坐标;
(3)CD
为
x
轴上一条动线段,D
在
C
点右边且
CD=1,求当
AC+CD+DB
的最小值和此时
C
点的坐标;
点
C
为∠AOB
内一点.(1)在
OA
求作点
D,OB
上求作点
E,使△CDE
的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE
周长的最小值和此时∠DCE
的度数.
11.(1)如图①,△ABD
和△ACE
均为等边三角形,BE、CE
交于
F,连
AF,求证:AF+BF+CF=CD;(2)在△ABC
中,∠ABC=30°,AB=6,BC=8,∠A,∠C
均小于
120°,求作一点
P,使
PA+PB+PC
的值最小,试求出最小值并说明理由.
12.荆州护城河在
CC'处直角转弯,河宽相等,从
A
处到达
B
处,需经过两座桥
DD'、EE',护城河及两
桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使
A
到
B
点路径最短?
PAGE
