人教版 八年级数学上册 13.1 轴对称 优化训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 13.1 轴对称 优化训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 588.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 20:35:33 | ||
图片预览



文档简介
人教版 八年级数学上册 13.1 轴对称 优化训练
一、选择题
1. 下列倡导节约的图案中,属于轴对称图形的是( )
2. 在下列图形中是轴对称图形的是( )
3. P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是 ( )
A. OP1⊥OP2 B. OP1=OP2
C. OP1⊥OP2且OP1=OP2 D. OP1≠OP2
4. 如图,线段AB与A'B'(AB=A'B')不关于直线l成轴对称的是 ( )
5. 若点A(2m,2-m)和点B(3+n,n)关于y轴对称,则m,n的值分别为( )
A.1,-1 B.,
C.-5,7 D.-,-
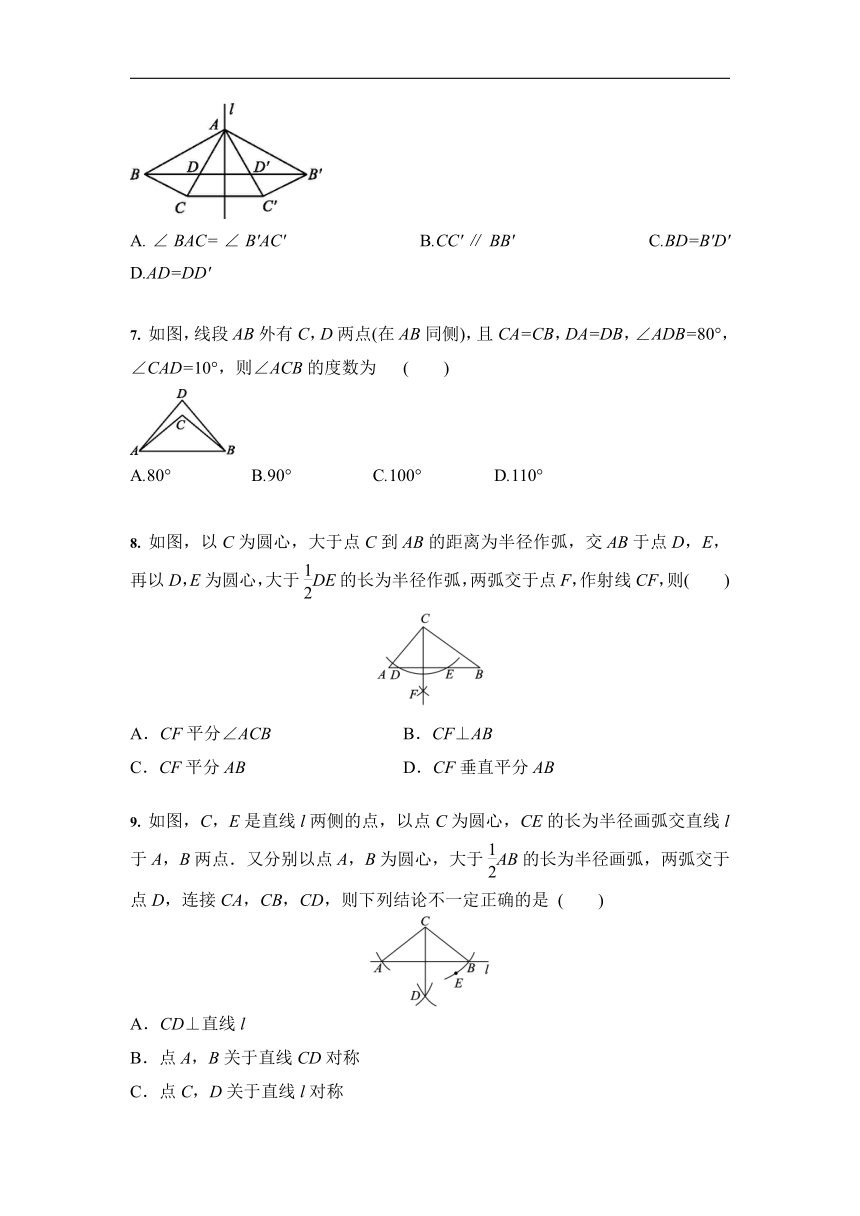
6. 如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是( )
A.∠BAC=∠B'AC' B.CC'∥BB' C.BD=B'D' D.AD=DD'
7. 如图,线段AB外有C,D两点(在AB同侧),且CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为 ( )
A.80° B.90° C.100° D.110°
8. 如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB B.CF⊥AB
C.CF平分AB D.CF垂直平分AB
9. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
10. 图中序号(1)(2)(3)(4)对应的四个三角形都是由△ABC进行了一次变换之后得到的,其中是通过轴对称变换得到的是 ( )
A.(1) B.(2) C.(3) D.(4)
二、填空题
11. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
12. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
13. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
14. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).?
三、作图题
15. 如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
四、解答题
16. 图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
17. 如图,在△ABE中,AD⊥BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19. 如图,DF为△ABC的边BC的垂直平分线,F为垂足,DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,且AB>AC,连接BD,CD.求证:
(1)∠DBE=∠DCA;
(2)BE=AC+AE.
人教版 八年级数学上册 13.1 轴对称 优化训练-答案
一、选择题
1. 【答案】B
2. 【答案】B
3. 【答案】 B
4. 【答案】A [解析] 选项A中,A'B'是由线段AB平移得到的,所以线段AB与A'B'不关于直线l成轴对称.
5. 【答案】C [解析] ∵点A(2m,2-m)和点B(3+n,n)关于y轴对称,∴2m+3+n=0,2-m=n,解得m=-5,n=7.
6. 【答案】D [解析] 如图,设BB'交直线l于点O.
∵△ABC与△AB'C'关于直线l对称,
∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',OD=OD',OB=OB'.
∴∠BAC=∠B'AC',BB'∥CC',BD=B'D'.
故选项A,B,C正确.故选D.
7. 【答案】C
8. 【答案】B
9. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
10. 【答案】A
二、填空题
11. 【答案】3 2 2
12. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得因为m为整数,所以m=2.
13. 【答案】3 [解析] ∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
14. 【答案】③
三、作图题
15. 【答案】
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,
∴OA=OB.
同理,OA=OC.
∴OB=OC.
四、解答题
16. 【答案】
[解析] 因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
17. 【答案】
解:∵BD=DC,AD⊥BE,∴AB=AC.
∵点C在AE的垂直平分线上,∴AC=CE.
∵△ABC的周长是22 cm,
∴AC+AB+BD+CD=22 cm.
∴AC+CD=11 cm.
∴DE=CD+CE=CD+AC=11 cm.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19. 【答案】
证明:(1)如图,过点D作DG⊥CA交CA的延长线于点G.
∵DF是BC的垂直平分线,∴BD=CD.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠DEB=∠DGC=90°.
在Rt△DBE和Rt△DCG中,
∴Rt△DBE≌Rt△DCG(HL).
∴∠DBE=∠DCA.
(2)∵Rt△DBE≌Rt△DCG,∴BE=CG.
在Rt△DEA和Rt△DGA中,
∴Rt△DEA≌Rt△DGA(HL).
∴AE=AG.
∴BE=CG=AC+AG=AC+AE,
即BE=AC+AE.
一、选择题
1. 下列倡导节约的图案中,属于轴对称图形的是( )
2. 在下列图形中是轴对称图形的是( )
3. P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是 ( )
A. OP1⊥OP2 B. OP1=OP2
C. OP1⊥OP2且OP1=OP2 D. OP1≠OP2
4. 如图,线段AB与A'B'(AB=A'B')不关于直线l成轴对称的是 ( )
5. 若点A(2m,2-m)和点B(3+n,n)关于y轴对称,则m,n的值分别为( )
A.1,-1 B.,
C.-5,7 D.-,-
6. 如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是( )
A.∠BAC=∠B'AC' B.CC'∥BB' C.BD=B'D' D.AD=DD'
7. 如图,线段AB外有C,D两点(在AB同侧),且CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为 ( )
A.80° B.90° C.100° D.110°
8. 如图,以C为圆心,大于点C到AB的距离为半径作弧,交AB于点D,E,再以D,E为圆心,大于DE的长为半径作弧,两弧交于点F,作射线CF,则( )
A.CF平分∠ACB B.CF⊥AB
C.CF平分AB D.CF垂直平分AB
9. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
10. 图中序号(1)(2)(3)(4)对应的四个三角形都是由△ABC进行了一次变换之后得到的,其中是通过轴对称变换得到的是 ( )
A.(1) B.(2) C.(3) D.(4)
二、填空题
11. 如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
12. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
13. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是________.
14. 数学活动课上,两名同学围绕作图问题:“如图①,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形,其中作法正确的为图 (填“②”或“③”).?
三、作图题
15. 如图,已知△ABC.
(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;
(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.
四、解答题
16. 图中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
17. 如图,在△ABE中,AD⊥BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19. 如图,DF为△ABC的边BC的垂直平分线,F为垂足,DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,且AB>AC,连接BD,CD.求证:
(1)∠DBE=∠DCA;
(2)BE=AC+AE.
人教版 八年级数学上册 13.1 轴对称 优化训练-答案
一、选择题
1. 【答案】B
2. 【答案】B
3. 【答案】 B
4. 【答案】A [解析] 选项A中,A'B'是由线段AB平移得到的,所以线段AB与A'B'不关于直线l成轴对称.
5. 【答案】C [解析] ∵点A(2m,2-m)和点B(3+n,n)关于y轴对称,∴2m+3+n=0,2-m=n,解得m=-5,n=7.
6. 【答案】D [解析] 如图,设BB'交直线l于点O.
∵△ABC与△AB'C'关于直线l对称,
∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',OD=OD',OB=OB'.
∴∠BAC=∠B'AC',BB'∥CC',BD=B'D'.
故选项A,B,C正确.故选D.
7. 【答案】C
8. 【答案】B
9. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
10. 【答案】A
二、填空题
11. 【答案】3 2 2
12. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得
13. 【答案】3 [解析] ∵AD平分∠BAC,且DE⊥AB,∠C=90°,∴CD=DE=1.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠B=∠DAB.
∵∠DAB=∠CAD,
∴∠CAD=∠DAB=∠B.
∵∠C=90°,∴∠CAD+∠DAB+∠B=90°.
∴∠B=30°.∴BD=2DE=2.
∴BC=BD+CD=2+1=3.
14. 【答案】③
三、作图题
15. 【答案】
解:(1)如图所示.
(2)证明:如图,连接OA.
∵l1是AB的垂直平分线,
∴OA=OB.
同理,OA=OC.
∴OB=OC.
四、解答题
16. 【答案】
[解析] 因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
17. 【答案】
解:∵BD=DC,AD⊥BE,∴AB=AC.
∵点C在AE的垂直平分线上,∴AC=CE.
∵△ABC的周长是22 cm,
∴AC+AB+BD+CD=22 cm.
∴AC+CD=11 cm.
∴DE=CD+CE=CD+AC=11 cm.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19. 【答案】
证明:(1)如图,过点D作DG⊥CA交CA的延长线于点G.
∵DF是BC的垂直平分线,∴BD=CD.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠DEB=∠DGC=90°.
在Rt△DBE和Rt△DCG中,
∴Rt△DBE≌Rt△DCG(HL).
∴∠DBE=∠DCA.
(2)∵Rt△DBE≌Rt△DCG,∴BE=CG.
在Rt△DEA和Rt△DGA中,
∴Rt△DEA≌Rt△DGA(HL).
∴AE=AG.
∴BE=CG=AC+AG=AC+AE,
即BE=AC+AE.
