人教版 八年级数学上册 13.2 画轴对称图形 优化训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 13.2 画轴对称图形 优化训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 447.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览



文档简介
人教版 八年级数学上册 13.2 画轴对称图形 优化训练
一、选择题
1. 如图,长方形的一条对称轴是( )
A.直线l1 B.直线l2
C.直线l3 D.直线l4
2. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是( )
A.(-2,1) B.(-1,1)
C.(1,-2) D.(-1,-2)
3. 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴的对称图形△A2B2C2,则顶点A2的坐标是( )
A.(-3,2) B.(2,-3)
C.(1,-2) D.(3,-1)
4. 2019·都江堰模拟如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则下列结论不正确的是( )
A.AO=BO B.MN⊥AB
C.AN=BN D.AB=2CO
5. 在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是 ( )
A.(4,1) B.(-1,4) C.(-4,-1) D.(-1,-4)
6. 如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
A.40° B.45°
C.50° D.60°
7. 如,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出 ( )
A.1个 B.2个 C.3个 D.4个
8. 在平面直角坐标系中,已知在y轴与直线x=3之间有一点M(a,3).如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为 ( )
A.4 B.3 C.2 D.1
9. 若△ABC的三个顶点的横坐标不变,纵坐标都乘-1,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴负方向平移1个单位长度
D.将原图形沿y轴负方向平移1个单位长度
10. 如图,在直角坐标系xOy中,直线y=1是△ABC的对称轴,已知点A的坐标是(4,4),则点B的坐标是 ( )
图13-2-7
A.(4,-4) B.(-4,2) C.(4,-2) D.(-2,4)
二、作图题
11. 利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
12. 分析与操作如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
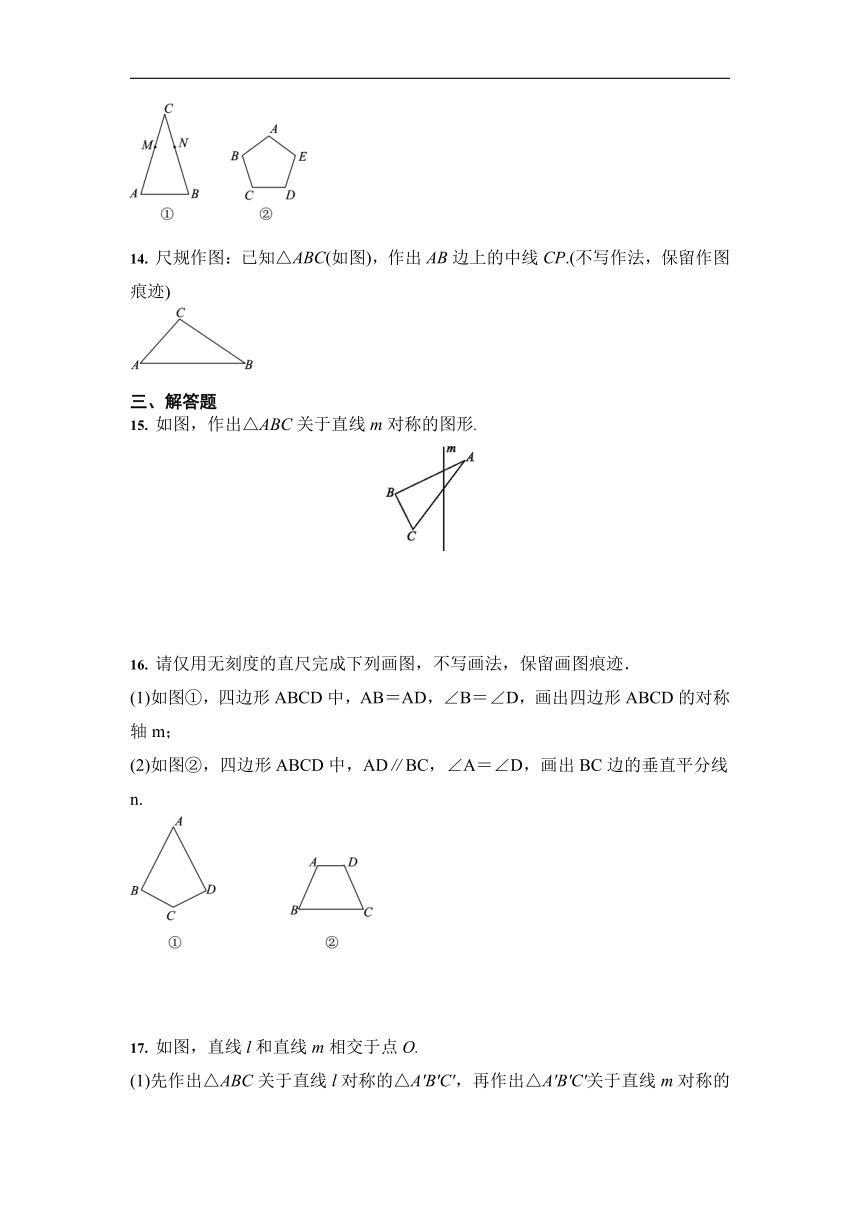
13. (1)在图①中,CA=CB,CM=CN,请用无刻度的直尺画出△ABC的对称轴;
(2)在图②中,已知正五边形ABCDE,请用无刻度的直尺画出它的一条对称轴.
14. 尺规作图:已知△ABC(如图),作出AB边上的中线CP.(不写作法,保留作图痕迹)
三、解答题
15. 如图,作出△ABC关于直线m对称的图形.
16. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
17. 如图,直线l和直线m相交于点O.
(1)先作出△ABC关于直线l对称的△A'B'C',再作出△A'B'C'关于直线m对称的△A1B1C1;
(2)△ABC与△A1B1C1关于某条直线对称吗?若对称,请画出对称轴.
18. (1)如图①,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图②,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且点A与点C是对称点,标明对称轴b,并简述画图过程.
(3)如图③,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
人教版 八年级数学上册 13.2 画轴对称图形 优化训练-答案
一、选择题
1. 【答案】B
2. 【答案】B [解析] 根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
3. 【答案】B 解析:顶点A的坐标是(-2,3),△ABC向右平移4个单位后得到△A1B1C1的顶点A1的坐标是(2,3),△A1B1C1关于x轴对称图形△A2B2C2的顶点A2的坐标是(2,-3).
4. 【答案】D [解析] 由作法得MN垂直平分AB,
∴OA=OB,MN⊥AB,AN=BN,只有选项D不成立.
5. 【答案】A
6. 【答案】C [解析] 由作法得CG⊥AB.
∵AC=BC,∴CG平分∠ACB,∠A=∠B=40°.
∵∠ACB=180°-∠A-∠B=100°,
∴∠BCG=∠ACB=50°.
7. 【答案】C [解析] 符合题意的三角形有3个,如图.
8. 【答案】D [解析] ∵该点关于直线x=3的对称点N的坐标为(5,3),∴对称点到直线x=3的距离为5-3=2.
又∵点M(a,3)到直线x=3的距离为3-a,
∴3-a=2.∴a=1.
9. 【答案】A [解析] ∵纵坐标乘-1,
∴变化前后纵坐标互为相反数.
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选A.
10. 【答案】C [解析] 根据题意,得点A和点B是关于直线y=1对称的点,它们到直线y=1的距离相等,都是3个单位长度,所以点B的坐标是(4,-2).
二、作图题
11. 【答案】
解:如图,四边形A1B1C1D1即为所求.
12. 【答案】
如图所示,①作两条公路夹角的平分线OD,OE;
②作线段AB的垂直平分线FG,则射线OD,OE与直线FG的交点C1,C2即为所求的位置.
13. 【答案】
解:(1)如图①,直线CD即为所求.
(2)答案不唯一,如图②,直线OA即为所求.
14. 【答案】
解:如图所示,CP即为所求.
三、解答题
15. 【答案】
解:如图所示,△A'B'C'即为所求.
16. 【答案】
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
17. 【答案】
解:(1)如图所示:
(2)由图可知,△ABC与△A1B1C1不关于某条直线对称.
18. 【答案】
解:(1)这两条线段一定关于某条直线对称,对称轴a如图①所示.
(2)如图②所示.
(ⅰ)连接AC;
(ⅱ)作线段AC的垂直平分线,即为对称轴b;
(ⅲ)作点B关于直线b的对称点D;
(ⅳ)连接CD,线段CD即为所求.
(3)能.操作方法(不唯一):如图③所示,连接BD;作线段BD的垂直平分线,即为对称轴c;作点C关于直线c的对称点E;连接BE;作∠ABE的平分线,角平分线所在的直线d即为对称轴,
故其中一条线段作两次轴对称即可使它与另一条线段重合.
一、选择题
1. 如图,长方形的一条对称轴是( )
A.直线l1 B.直线l2
C.直线l3 D.直线l4
2. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是( )
A.(-2,1) B.(-1,1)
C.(1,-2) D.(-1,-2)
3. 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴的对称图形△A2B2C2,则顶点A2的坐标是( )
A.(-3,2) B.(2,-3)
C.(1,-2) D.(3,-1)
4. 2019·都江堰模拟如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则下列结论不正确的是( )
A.AO=BO B.MN⊥AB
C.AN=BN D.AB=2CO
5. 在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是 ( )
A.(4,1) B.(-1,4) C.(-4,-1) D.(-1,-4)
6. 如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为( )
A.40° B.45°
C.50° D.60°
7. 如,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出 ( )
A.1个 B.2个 C.3个 D.4个
8. 在平面直角坐标系中,已知在y轴与直线x=3之间有一点M(a,3).如果该点关于直线x=3的对称点N的坐标为(5,3),那么a的值为 ( )
A.4 B.3 C.2 D.1
9. 若△ABC的三个顶点的横坐标不变,纵坐标都乘-1,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴负方向平移1个单位长度
D.将原图形沿y轴负方向平移1个单位长度
10. 如图,在直角坐标系xOy中,直线y=1是△ABC的对称轴,已知点A的坐标是(4,4),则点B的坐标是 ( )
图13-2-7
A.(4,-4) B.(-4,2) C.(4,-2) D.(-2,4)
二、作图题
11. 利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
12. 分析与操作如图,有公路l1同侧、l2异侧的两个城镇A,B,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不写作法)
13. (1)在图①中,CA=CB,CM=CN,请用无刻度的直尺画出△ABC的对称轴;
(2)在图②中,已知正五边形ABCDE,请用无刻度的直尺画出它的一条对称轴.
14. 尺规作图:已知△ABC(如图),作出AB边上的中线CP.(不写作法,保留作图痕迹)
三、解答题
15. 如图,作出△ABC关于直线m对称的图形.
16. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
17. 如图,直线l和直线m相交于点O.
(1)先作出△ABC关于直线l对称的△A'B'C',再作出△A'B'C'关于直线m对称的△A1B1C1;
(2)△ABC与△A1B1C1关于某条直线对称吗?若对称,请画出对称轴.
18. (1)如图①,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图②,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且点A与点C是对称点,标明对称轴b,并简述画图过程.
(3)如图③,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
人教版 八年级数学上册 13.2 画轴对称图形 优化训练-答案
一、选择题
1. 【答案】B
2. 【答案】B [解析] 根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
3. 【答案】B 解析:顶点A的坐标是(-2,3),△ABC向右平移4个单位后得到△A1B1C1的顶点A1的坐标是(2,3),△A1B1C1关于x轴对称图形△A2B2C2的顶点A2的坐标是(2,-3).
4. 【答案】D [解析] 由作法得MN垂直平分AB,
∴OA=OB,MN⊥AB,AN=BN,只有选项D不成立.
5. 【答案】A
6. 【答案】C [解析] 由作法得CG⊥AB.
∵AC=BC,∴CG平分∠ACB,∠A=∠B=40°.
∵∠ACB=180°-∠A-∠B=100°,
∴∠BCG=∠ACB=50°.
7. 【答案】C [解析] 符合题意的三角形有3个,如图.
8. 【答案】D [解析] ∵该点关于直线x=3的对称点N的坐标为(5,3),∴对称点到直线x=3的距离为5-3=2.
又∵点M(a,3)到直线x=3的距离为3-a,
∴3-a=2.∴a=1.
9. 【答案】A [解析] ∵纵坐标乘-1,
∴变化前后纵坐标互为相反数.
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选A.
10. 【答案】C [解析] 根据题意,得点A和点B是关于直线y=1对称的点,它们到直线y=1的距离相等,都是3个单位长度,所以点B的坐标是(4,-2).
二、作图题
11. 【答案】
解:如图,四边形A1B1C1D1即为所求.
12. 【答案】
如图所示,①作两条公路夹角的平分线OD,OE;
②作线段AB的垂直平分线FG,则射线OD,OE与直线FG的交点C1,C2即为所求的位置.
13. 【答案】
解:(1)如图①,直线CD即为所求.
(2)答案不唯一,如图②,直线OA即为所求.
14. 【答案】
解:如图所示,CP即为所求.
三、解答题
15. 【答案】
解:如图所示,△A'B'C'即为所求.
16. 【答案】
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
17. 【答案】
解:(1)如图所示:
(2)由图可知,△ABC与△A1B1C1不关于某条直线对称.
18. 【答案】
解:(1)这两条线段一定关于某条直线对称,对称轴a如图①所示.
(2)如图②所示.
(ⅰ)连接AC;
(ⅱ)作线段AC的垂直平分线,即为对称轴b;
(ⅲ)作点B关于直线b的对称点D;
(ⅳ)连接CD,线段CD即为所求.
(3)能.操作方法(不唯一):如图③所示,连接BD;作线段BD的垂直平分线,即为对称轴c;作点C关于直线c的对称点E;连接BE;作∠ABE的平分线,角平分线所在的直线d即为对称轴,
故其中一条线段作两次轴对称即可使它与另一条线段重合.
