人教版 九年级数学上册 24.1 圆的有关性质 优化训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学上册 24.1 圆的有关性质 优化训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 641.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 20:58:18 | ||
图片预览


文档简介
人教版 九年级数学上册 24.1 圆的有关性质 优化训练
一、选择题
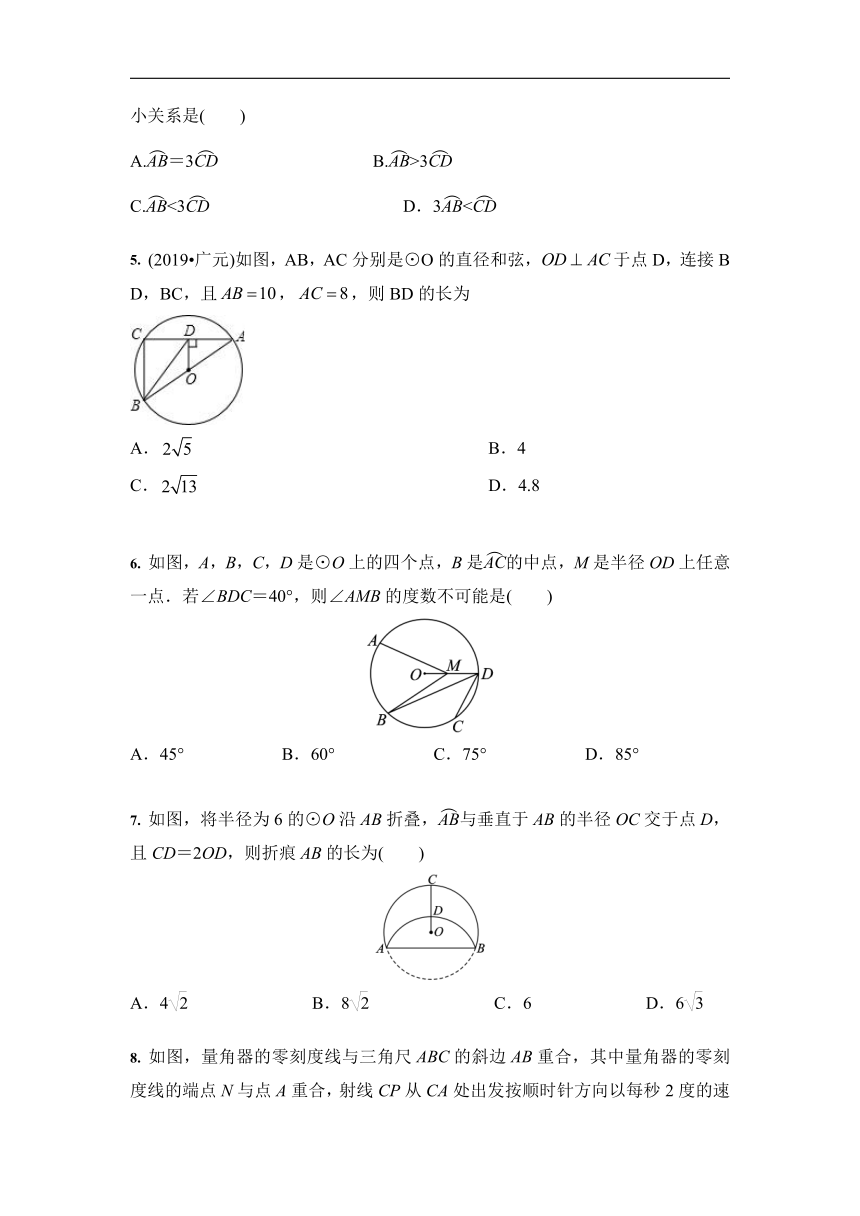
1. (2019?贵港)如图,是的直径,,若,则圆周角的度数是
A. B.C. D.
2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )
A.OE=BE B.=
C.△BOC是等边三角形 D.四边形ODBC是菱形
3. (2019?吉林)如图,在中,所对的圆周角,若为上一点,,则的度数为
A.30° B.45°C.55° D.60°
4. 在⊙O中,圆心角∠AOB=3∠COD(∠COD<60°),则劣弧AB,劣弧CD的大小关系是( )
A.=3 B.>3
C.<3 D.3<
5. (2019?广元)如图,AB,AC分别是⊙O的直径和弦,于点D,连接BD,BC,且,,则BD的长为
A. B.4C. D.4.8
6. 如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45° B.60° C.75° D.85°
7. 如图,将半径为6的⊙O沿AB折叠,与垂直于AB的半径OC交于点D,且CD=2OD,则折痕AB的长为( )
A.4 B.8 C.6 D.6
8. 如图,量角器的零刻度线与三角尺ABC的斜边AB重合,其中量角器的零刻度线的端点N与点A重合,射线CP从CA处出发按顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是( )
A.48° B.64° C.96° D.132°
9. (2019?镇江)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于
A. B.C. D.
10. 如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
二、填空题
11. 如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=________°.
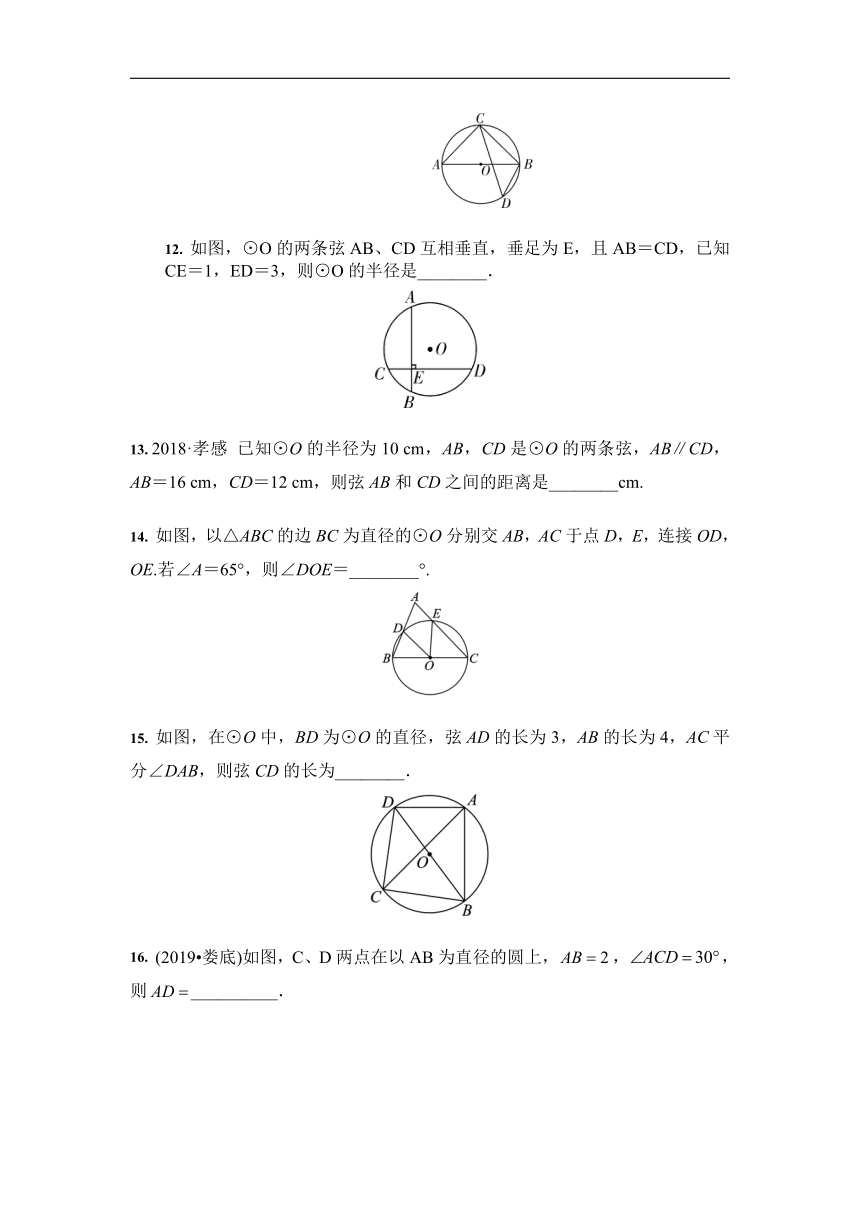
12. 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是________.
13. 2018·孝感 已知⊙O的半径为10 cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是________cm.
14. 如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
15. 如图,在⊙O中,BD为⊙O的直径,弦AD的长为3,AB的长为4,AC平分∠DAB,则弦CD的长为________.
16. (2019?娄底)如图,C、D两点在以AB为直径的圆上,,,则__________.
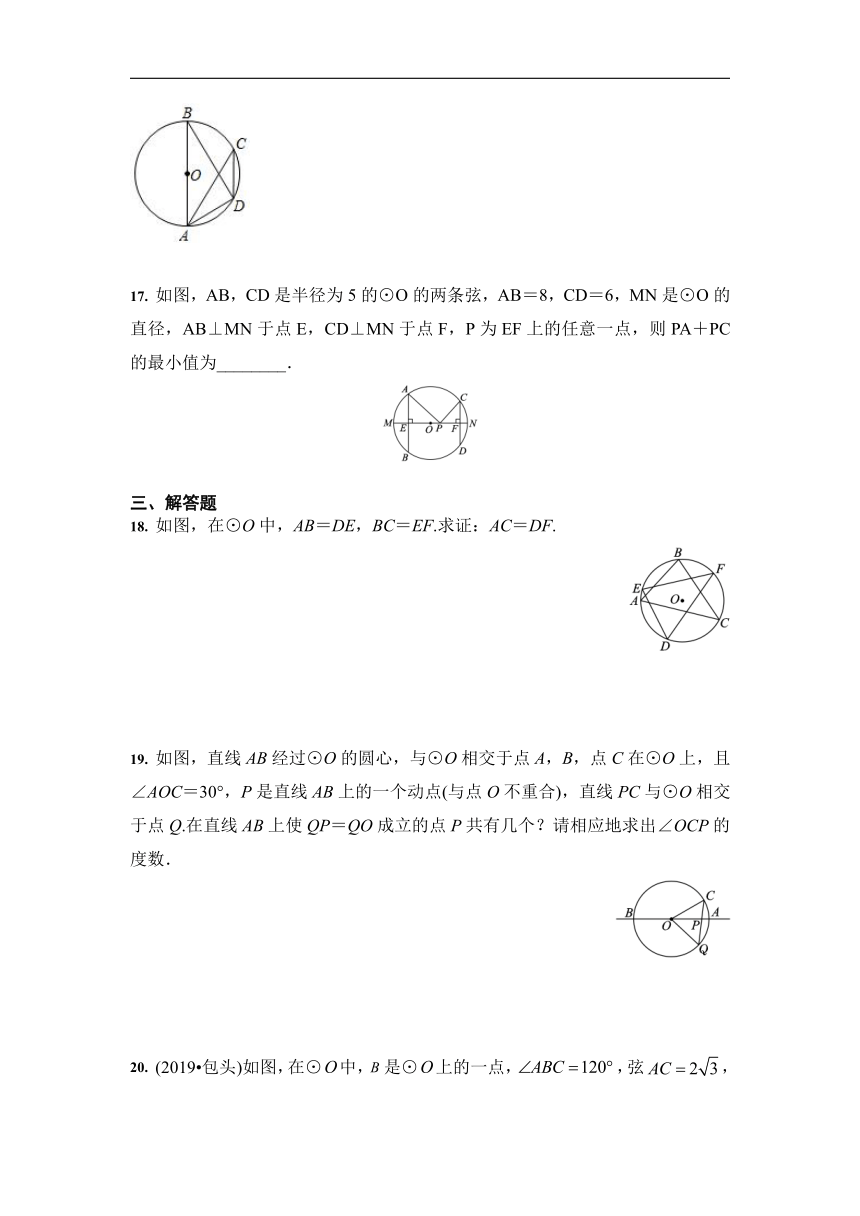
17. 如图,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是⊙O的直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为________.
三、解答题
18. 如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
19. 如图,直线AB经过⊙O的圆心,与⊙O相交于点A,B,点C在⊙O上,且∠AOC=30°,P是直线AB上的一个动点(与点O不重合),直线PC与⊙O相交于点Q.在直线AB上使QP=QO成立的点P共有几个?请相应地求出∠OCP的度数.
20. (2019?包头)如图,在⊙中,是⊙上的一点,,弦,弦平分交于点,连接.
(1)求⊙半径的长;
(2)求证:.
人教版 九年级数学上册 24.1 圆的有关性质 优化训练-答案
一、选择题
1. 【答案】B
【解析】∵,,∴,
∵,∴,
∴,故选B.
2. 【答案】B [解析] AB是⊙O的直径,弦CD⊥AB于点E,由垂径定理可以得到CE=DE,=,=.但并不一定能得到OE=BE,OC=BC,从而A,C,D选项都是错误的.
故选B.
3. 【答案】B
【解析】∵∠ACB=50°,∴∠AOB=2∠ACB=100°,∵∠AOP=55°,∴∠POB=45°,故选B.
4. 【答案】A [解析] 把∠AOB三等分,得到的每一份角所对的弧都等于,因此有=3.
5. 【答案】C
【解析】∵AB为直径,∴,∴,
∵,∴,
在中,.故选C.
6. 【答案】D [解析] 连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
7. 【答案】B [解析] 如图,延长CO交AB于点E,连接OB.∵CE⊥AB,∴AB=2BE.∵OC=6,CD=2OD,∴CD=4,OD=2,OB=6.由折叠的性质可得DE=×(6×2-4)=4,
∴OE=DE-OD=4-2=2.在Rt△OEB中,BE===4 ,
∴AB=8 .故选B.
8. 【答案】C [解析] ∵∠ACB=90°,∴点C在以O为圆心,OA长为半径的圆上.第24秒时,∠ACE=48°,∴∠EOA=2∠ACE=96°.
9. 【答案】A
【解析】如图,连接AC,
∵四边形ABCD是半圆的内接四边形,∴∠DAB=180°–∠C=70°,
∵,∴∠CAB=∠DAB=35°,
∵AB是直径,∴∠ACB=90°,∴∠ABC=90°–∠CAB=55°,故选A.
10. 【答案】C
二、填空题
11. 【答案】62 【解析】根据直径所对的圆周角等于90°及∠BCD=28°,可得∠ACD=∠ACB-∠BCD=90°-28°=62°,再根据同弧所对圆周角相等有∠ABD=∠ACD=62°.
12. 【答案】 【解析】本题考查垂径定理、弦、弦心距的性质、正方形的判定与性质、勾股定理等内容. 解题思路:过点O作OF⊥AB,OG⊥CD,垂足分别是F、G. 连接OD.
解图
?
?OG=GE=1?OD===.
13. 【答案】2或14 [解析] ①当弦AB和CD在圆心同侧时,连接OA,OC,过点O作OE⊥CD于点F,交AB于点E,如图①,
∵AB=16 cm,CD=12 cm,
∴AE=8 cm,CF=6 cm.
∵OA=OC=10 cm,
∴EO=6 cm,OF=8 cm,
∴EF=OF-OE=2 cm;
②当弦AB和CD在圆心异侧时,连接OA,OC,过点O作OE⊥CD于点E并反向延长交AB于点F,如图②,∵AB=16 cm,CD=12 cm,
∴AF=8 cm,CE=6 cm.
∵OA=OC=10 cm,
∴OF=6 cm,OE=8 cm,
∴EF=OF+OE=14 cm.
∴AB与CD之间的距离为2 cm或14 cm.
14. 【答案】50 [解析] 由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
15. 【答案】 [解析] ∵BD为⊙O的直径,
∴∠DAB=∠DCB=90°.
∵AD=3,AB=4,∴BD=5.
又∵AC平分∠DAB,∴∠DAC=∠BAC=45°,
∴∠DBC=∠DAC=45°,∠CDB=∠BAC=45°,
从而CD=CB,∴CD= .
16. 【答案】1
【解析】∵AB为直径,∴,∵,∴.
故答案为:1.
17. 【答案】7 [解析] 如图,连接OB,OC,BC,则BC的长即为PA+PC的最小值.过点C作CH⊥AB于点H,则四边形EFCH为矩形,
∴CH=EF,EH=CF.根据垂径定理,得BE=AB=4,CF=CD=3,
∴OE===3,OF===4,
∴CH=EF=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7.
在Rt△BCH中,由勾股定理,得BC=7 ,则PA+PC的最小值为7 .
三、解答题
18. 【答案】
证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
19. 【答案】
解:在直线AB上使QP=QO成立的点P共有3个.
(1)如图①.
在△QOC中,OC=OQ,∴∠OQC=∠OCQ.
在△OPQ中,QP=QO,∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,且∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCQ=120°,
∴∠OCQ=40°.
即∠OCP=40°.
(2)如图②.
∵QO=QP,
∴∠QPO=∠QOP.
设∠QPO=x,则∠OQC=∠QPO+∠QOP=2x.又∵OC=OQ,
∴∠OCQ=∠OQC=2x,
∴∠AOC=∠OPC+∠OCP=x+2x=3x.
∵∠AOC=30°,∴3x=30°,解得x=10°,
∴∠OCP=2x=20°.
(3)如图③.
∵QO=QP,∴∠QOP=∠QPO.
∵OC=OQ,∴∠OQC=∠OCQ.
设∠QPO=y,则∠OQC=∠OCQ=∠QPO+∠AOC=y+30°,
∴在△OPQ中,有y+y+y+30°=180°,解得y=50°,
∴∠OCP=180°-50°-30°=100°.
综上所述,在直线AB上使QP=QO成立的点P共有3个,∠OCP的度数分别为40°,20°,100°.
20. 【答案】
(1)连接,过作于点,如图1,
∵,
∴,
∴,
∴,
∵,
∴,
故⊙的半径为.
(2)在上截取,连接,如图2,
∵,平分,
∴,
∵,
∴是等边三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴,
∵,
∴.
一、选择题
1. (2019?贵港)如图,是的直径,,若,则圆周角的度数是
A. B.C. D.
2. 如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )
A.OE=BE B.=
C.△BOC是等边三角形 D.四边形ODBC是菱形
3. (2019?吉林)如图,在中,所对的圆周角,若为上一点,,则的度数为
A.30° B.45°C.55° D.60°
4. 在⊙O中,圆心角∠AOB=3∠COD(∠COD<60°),则劣弧AB,劣弧CD的大小关系是( )
A.=3 B.>3
C.<3 D.3<
5. (2019?广元)如图,AB,AC分别是⊙O的直径和弦,于点D,连接BD,BC,且,,则BD的长为
A. B.4C. D.4.8
6. 如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45° B.60° C.75° D.85°
7. 如图,将半径为6的⊙O沿AB折叠,与垂直于AB的半径OC交于点D,且CD=2OD,则折痕AB的长为( )
A.4 B.8 C.6 D.6
8. 如图,量角器的零刻度线与三角尺ABC的斜边AB重合,其中量角器的零刻度线的端点N与点A重合,射线CP从CA处出发按顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是( )
A.48° B.64° C.96° D.132°
9. (2019?镇江)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于
A. B.C. D.
10. 如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
二、填空题
11. 如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD=________°.
12. 如图,⊙O的两条弦AB、CD互相垂直,垂足为E,且AB=CD,已知CE=1,ED=3,则⊙O的半径是________.
13. 2018·孝感 已知⊙O的半径为10 cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16 cm,CD=12 cm,则弦AB和CD之间的距离是________cm.
14. 如图,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE=________°.
15. 如图,在⊙O中,BD为⊙O的直径,弦AD的长为3,AB的长为4,AC平分∠DAB,则弦CD的长为________.
16. (2019?娄底)如图,C、D两点在以AB为直径的圆上,,,则__________.
17. 如图,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是⊙O的直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为________.
三、解答题
18. 如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
19. 如图,直线AB经过⊙O的圆心,与⊙O相交于点A,B,点C在⊙O上,且∠AOC=30°,P是直线AB上的一个动点(与点O不重合),直线PC与⊙O相交于点Q.在直线AB上使QP=QO成立的点P共有几个?请相应地求出∠OCP的度数.
20. (2019?包头)如图,在⊙中,是⊙上的一点,,弦,弦平分交于点,连接.
(1)求⊙半径的长;
(2)求证:.
人教版 九年级数学上册 24.1 圆的有关性质 优化训练-答案
一、选择题
1. 【答案】B
【解析】∵,,∴,
∵,∴,
∴,故选B.
2. 【答案】B [解析] AB是⊙O的直径,弦CD⊥AB于点E,由垂径定理可以得到CE=DE,=,=.但并不一定能得到OE=BE,OC=BC,从而A,C,D选项都是错误的.
故选B.
3. 【答案】B
【解析】∵∠ACB=50°,∴∠AOB=2∠ACB=100°,∵∠AOP=55°,∴∠POB=45°,故选B.
4. 【答案】A [解析] 把∠AOB三等分,得到的每一份角所对的弧都等于,因此有=3.
5. 【答案】C
【解析】∵AB为直径,∴,∴,
∵,∴,
在中,.故选C.
6. 【答案】D [解析] 连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
7. 【答案】B [解析] 如图,延长CO交AB于点E,连接OB.∵CE⊥AB,∴AB=2BE.∵OC=6,CD=2OD,∴CD=4,OD=2,OB=6.由折叠的性质可得DE=×(6×2-4)=4,
∴OE=DE-OD=4-2=2.在Rt△OEB中,BE===4 ,
∴AB=8 .故选B.
8. 【答案】C [解析] ∵∠ACB=90°,∴点C在以O为圆心,OA长为半径的圆上.第24秒时,∠ACE=48°,∴∠EOA=2∠ACE=96°.
9. 【答案】A
【解析】如图,连接AC,
∵四边形ABCD是半圆的内接四边形,∴∠DAB=180°–∠C=70°,
∵,∴∠CAB=∠DAB=35°,
∵AB是直径,∴∠ACB=90°,∴∠ABC=90°–∠CAB=55°,故选A.
10. 【答案】C
二、填空题
11. 【答案】62 【解析】根据直径所对的圆周角等于90°及∠BCD=28°,可得∠ACD=∠ACB-∠BCD=90°-28°=62°,再根据同弧所对圆周角相等有∠ABD=∠ACD=62°.
12. 【答案】 【解析】本题考查垂径定理、弦、弦心距的性质、正方形的判定与性质、勾股定理等内容. 解题思路:过点O作OF⊥AB,OG⊥CD,垂足分别是F、G. 连接OD.
解图
?
?OG=GE=1?OD===.
13. 【答案】2或14 [解析] ①当弦AB和CD在圆心同侧时,连接OA,OC,过点O作OE⊥CD于点F,交AB于点E,如图①,
∵AB=16 cm,CD=12 cm,
∴AE=8 cm,CF=6 cm.
∵OA=OC=10 cm,
∴EO=6 cm,OF=8 cm,
∴EF=OF-OE=2 cm;
②当弦AB和CD在圆心异侧时,连接OA,OC,过点O作OE⊥CD于点E并反向延长交AB于点F,如图②,∵AB=16 cm,CD=12 cm,
∴AF=8 cm,CE=6 cm.
∵OA=OC=10 cm,
∴OF=6 cm,OE=8 cm,
∴EF=OF+OE=14 cm.
∴AB与CD之间的距离为2 cm或14 cm.
14. 【答案】50 [解析] 由三角形的内角和定理,得∠B+∠C=180°-∠A.再由OB=OD=OC=OE,得到∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
15. 【答案】 [解析] ∵BD为⊙O的直径,
∴∠DAB=∠DCB=90°.
∵AD=3,AB=4,∴BD=5.
又∵AC平分∠DAB,∴∠DAC=∠BAC=45°,
∴∠DBC=∠DAC=45°,∠CDB=∠BAC=45°,
从而CD=CB,∴CD= .
16. 【答案】1
【解析】∵AB为直径,∴,∵,∴.
故答案为:1.
17. 【答案】7 [解析] 如图,连接OB,OC,BC,则BC的长即为PA+PC的最小值.过点C作CH⊥AB于点H,则四边形EFCH为矩形,
∴CH=EF,EH=CF.根据垂径定理,得BE=AB=4,CF=CD=3,
∴OE===3,OF===4,
∴CH=EF=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7.
在Rt△BCH中,由勾股定理,得BC=7 ,则PA+PC的最小值为7 .
三、解答题
18. 【答案】
证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
19. 【答案】
解:在直线AB上使QP=QO成立的点P共有3个.
(1)如图①.
在△QOC中,OC=OQ,∴∠OQC=∠OCQ.
在△OPQ中,QP=QO,∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,且∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCQ=120°,
∴∠OCQ=40°.
即∠OCP=40°.
(2)如图②.
∵QO=QP,
∴∠QPO=∠QOP.
设∠QPO=x,则∠OQC=∠QPO+∠QOP=2x.又∵OC=OQ,
∴∠OCQ=∠OQC=2x,
∴∠AOC=∠OPC+∠OCP=x+2x=3x.
∵∠AOC=30°,∴3x=30°,解得x=10°,
∴∠OCP=2x=20°.
(3)如图③.
∵QO=QP,∴∠QOP=∠QPO.
∵OC=OQ,∴∠OQC=∠OCQ.
设∠QPO=y,则∠OQC=∠OCQ=∠QPO+∠AOC=y+30°,
∴在△OPQ中,有y+y+y+30°=180°,解得y=50°,
∴∠OCP=180°-50°-30°=100°.
综上所述,在直线AB上使QP=QO成立的点P共有3个,∠OCP的度数分别为40°,20°,100°.
20. 【答案】
(1)连接,过作于点,如图1,
∵,
∴,
∴,
∴,
∵,
∴,
故⊙的半径为.
(2)在上截取,连接,如图2,
∵,平分,
∴,
∵,
∴是等边三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴,
∵,
∴.
同课章节目录
