苏科版七年级数学上册 第2章 有理数 单元检测试题(Word版 含解析)
文档属性
| 名称 | 苏科版七年级数学上册 第2章 有理数 单元检测试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 51.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 21:05:56 | ||
图片预览




文档简介
1049020010693400123190000第2章 有理数 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
?1. 下列说法中,正确的是(? ? ? ? )
A.任何实数的平方都是正数
B.正数的倒数必小于这个正数
C.绝对值等于它本身的数必是非负数
D.零除以任何一个实数都等于零
?
2. 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数.从轻重的角度看,最接近标准的工件是(? ? ? ? )
A.-2 B.-3 C.3 D.5
?
3. 下列计算正确的是(? ? ? ? )
A.18÷(-3)2=-2? B.-23÷(-3)3=827
C.(-213)3=-8127? D.-3-12×1=-212
?
4. 下列实数中,无理数是(? ? ??)
A.16 B.8 C.17 D.3.14159
?
5. 计算84÷(-7)等于( )
A.-12 B.12 C.-14 D.14
?
6. 有理数a,b在数轴上的位置如图,则a-b是(? ? ? ? )
A.正数 B.负数 C.零 D.无法确定
?7. 下列各数中无理数是( )
A.π2 B.227 C.4 D.327
?
8. 下列各数中,数值相等的有( )
①32和23;②-23与(-2)3;③23与(-2)3;④-22与(-2)2;⑤-(-3)与-|-3|;⑥425与1625;⑦(-1)2017与-1;⑧-(-0.1)3与-0.001
A.1组 B.2组 C.3组 D.4组
二、 填空题 (本题共计 12 小题 ,每题 3 分 ,共计36分 , ) ?
9. 数轴上表示-5的点离表示+3的点的距离是________个单位长度.
?
10. 在数轴上距原点3个单位长度的点表示的数是________.
?
11. 若|a+2|+(b-2)2=0,则ab=________.
?
12. 若m,n互为相反数,则m+n-1=________.
?
13. 如果a=8,b=-5,且ab>0,则a+b=_________.
?
14. 若x-1=|-3|,那么x=________.
?
15. 绝对值小于2的整数是________.
?
16. 若x2=4,|y|=3,且xy<0,则x-y的值为________.
?
17. 已知|a|=7,|b|=3,且a+b>0,则a=________.
?
18. 绝对值不大于2的所有整数和是________.
?
19. 小天上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况(单位:元):
星期
一
二
三
四
五
每股涨跌
+4
+4.5
-1
-2.5
-6
星期五收盘时每股是________元,本周内最高价每股________元.
?
20. 有13张红心扑克牌(上面的点数从1到13,为正数),和13张黑花扑克牌(上面的点数从1到13,为负数),任意打乱顺序后,从上面第一张(红心8)开始作为被减数,然后依次把后面点数逐一相减,最后得数是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. (-212)÷(-5)×(-313).
?
22. 计算.
(1)(-378)÷(-7)÷(-9);??????
(2)3÷(-310)÷112;?????
(3)(-0.75)÷(-3)÷54.
?
23. 若(a+4)2+(b-2)2=0,求?2a+3b-6的值.
?
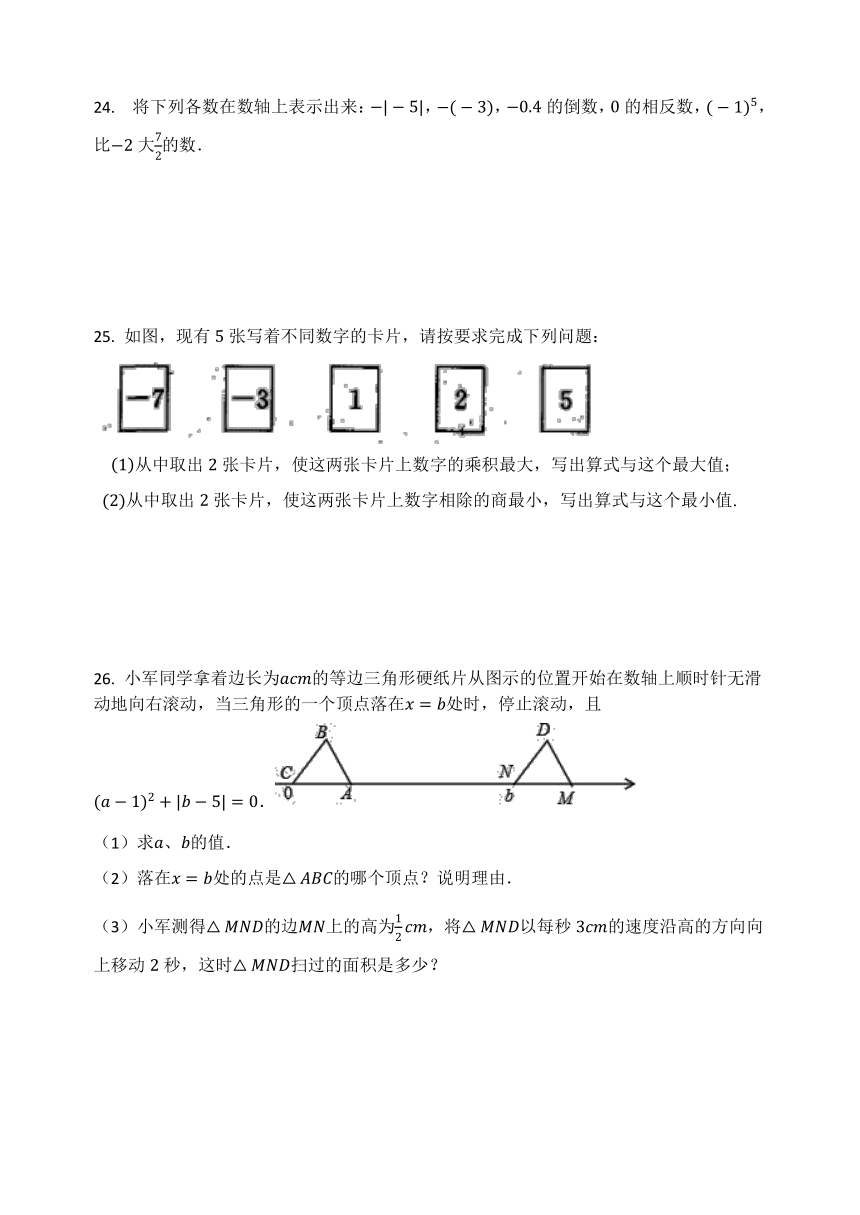
24. 将下列各数在数轴上表示出来:-|-5|,-(-3),-0.4的倒数,0的相反数,(-1)5,比-2大72的数.
?
25. 如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
1从中取出2张卡片,使这两张卡片上数字的乘积最大,写出算式与这个最大值;
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,写出算式与这个最小值.
?
26. 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
(1)求a、b的值.
(2)落在x=b处的点是△ABC的哪个顶点?说明理由.
(3)小军测得△MND的边MN上的高为12cm,将△MND以每秒3cm的速度沿高的方向向上移动2秒,这时△MND扫过的面积是多少?
参考答案与试题解析
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【解析】
此题暂无解析
【解答】
解:对于A,由于0的平方是0,而不是正数,故A错误;
对于B,由于1的倒数是1,故B错误;
对于C,由绝对值的性质可知,绝对值等于它本身的数必是非负数,故C正确;
对于D,当除数为0时,没有意义,故D错误.
故选C.
2.
【解析】
根据正负数的意义,绝对值最小的即为最接近标准的.
【解答】
解:|-2|=2,|-3|=3,|3|=3,|5|=5,
∵ 2<3<5,
∴ 从轻重的角度来看,最接近标准的记录为-2.
故选A.
3.
【解析】
根据有理数的乘方,有理数的乘除法,有理数的减法运算,即可算出正确结果。
【解答】
解:A,18÷-32=18÷9=2,所以A计算错误;
B,-23÷-33=-8÷-27=827,所以B计算正确;
C,-2133=-733=-34327=-121927,所以C计算错误;
D,-3-12×1=-3-12=-312,所以D计算错误.
故选B.
4.
【解析】
此题暂无解析
【解答】
解:A,16=4,是有理数;
B,8=22,是无理数;
C,17是分数,所以是有理数;
D,3.14159是有限小数,所以是有理数,
故选B.
5.
【解析】
根据有理数的除法运算法则,得出结果.
【解答】
解:84÷(-7)=-12.
故选A.
6.
【解析】
首先根据a、b点所在位置判断正负,再根据有理数的减法法则可知a-b=a+(-b),然后根据有理数的加法法则可判断出结果的正负.
【解答】
解:∵ a在原点左边,
∴ a<0,
∵ b在原点右边,
∴ b>0,
∴ a-b=a+(-b)<0.
故选B.
7.
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】
A、π2是无理数,故A正确;
B、227是有理数,故B错误;
C、4=2是有理数,故C错误;
D、327=3是有理数,故D错误;
8.
【解析】
分别对每组数值进行计算,再作出判断即可.
【解答】
∵ 32=9,23=8;
-23=-8,(-2)3=-8;
23=8,(-2)3=-8
-22=-4,(-2)2=4;
-(-3)=3,-|-3|=-3;
425=165≠1625;
(-1)2017=-1;
-(-0.1)3=0.001≠-0.001.
∴ ①中两数的数值不相等;
②中两数的数值相等;
③中两数的数值不相等;
④中两数的数值不相等;
⑤中两数的数值不相等;
⑥中两数的数值不相等;
⑦中两数的数值相等;
⑧中两数的数值不相等.
∴ 数值相等的有②⑦共2组
二、 填空题 (本题共计 12 小题 ,每题 3 分 ,共计36分 )
9.
【解析】
根据数轴上点的意义可知数轴上表示-5的点与表+3的点的距离是|-5-3|=8.
【解答】
解:数轴上表示-5的点离表示+3的点的距离是|-5-3|=8个单位长度;
故答案为:8.
10.
【解析】
在数轴上,+3和-3到原点0的距离都等于3,据此进行填空即可.
【解答】
在数轴上距原点3个单位长度的点表示的数是±3.
11.
【解析】
根据非负数的性质进行计算即可.
【解答】
解:∵ |a+2|+(b-2)2=0,
∴ a+2=0,b-2=0,
∴ a=-2,b=2,
∴ ab=(-2)2=4.
故答案为:4.
12.
【解析】
根据互为相反数的两个数的和等于0可得m+n=0,然后代入计算即可得解.
【解答】
解:∵ m,n互为相反数,
∴ m+n=0,
∴ m+n-1=0-1=-1.
故答案为:-1.
13.
【解析】
首先根据a的绝对值是8,确定出a=±8,再根据b为负数,且ab>0,得到a为负数,最后代入计算即可.
【解答】
解:∵ |a|=8,
∴ a=±8.
∵ b=-5,ab>0,
∴ a=-8,b=-5,
∴ a+b=-8-5=-13.
故答案为:-13.
14.
【解析】
根据绝对值的性质得出两个一元一次方程,再解方程,即可解答.
【解答】
解:∵ x-1=-3,
∴ x-1=3,
∴ x-1=3或x-1=-3,
∴ x=4或x=-2.
故答案为:4或-2.
15.
【解析】
可以根据数轴得到答案,到原点距离小于2的整数只有三个:-1,1,0.
【解答】
解:绝对值小于2的整数是:-1,0,1.
16.
【解析】
首先根据乘方和绝对值的性质可得x=±2,y=±3,再由xy<0可得x、y异号,然后再计算出x-y的值.
【解答】
解:∵ x2=4,|y|=3,
∴ x=±2,y=±3,
∵ xy<0,
∴ ①x=2,y=-3,x-y=5;
②x=-2,y=3,x-y=-5,
故答案为:±5.
17.
【解析】
先由绝对值的定义求出a、b的可能值,再根据有理数的加法法则确定a与b的对应值.
【解答】
解:∵ |a|=7,|b|=3,
∴ a=7或-7,b=3或-3,
又∵ a+b>0,
∴ a=7,b=3或-3.
故答案为:7.
18.
【解析】
找出绝对值不大于2的所有整数,求出之和即可.
【解答】
解:绝对值不大于2的所有整数是-2,-1,0,1,2,
之和为-2-1+0+1+2=0,
故答案为:0.
19.
【解析】
根据表格求出星期五的股价;求出每天的股价即可做出判断.
【解答】
解:根据表格得:每天的股价分别为:28+4=32(元),32+4.5=36.5(元),36.5-1=35.5(元),35.5-2.5=33(元),33-6=27(元),
(1)星期五收盘时每股27元;
(2)星期二每股价格最高,为36.5元.
故答案为:(1)27;(2)36.5
20.
【解析】
根据互为相反数的两个数的和等于0判断出最后只有红心8减去黑化8,再根据减去一个数等于加上这个数的相反数进行计算即可得解.
【解答】
解:∵ 互为相反数的两个数的和等于0,
∴ 最后得数为8-(-8),
=8+8,
=16.
故答案为:16.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【解析】
把带分数化为假分数,然后根据有理数的乘法运算法则进行计算即可得解.
【解答】
解:(-212)÷(-5)×(-313),
=-52×15×103,
=-53.
22.
【解析】
(1)按照“两数相除,同号的正,异号得负,并把绝对值相除”的法则直接计算即可;
(2)把除法转化成乘法,再进行约分即可;
(3)先把小数转化成分数,再把除法转化成乘法,然后约分即可.
【解答】
解;(1)(-378)÷(-7)÷(-9)
=54÷(-9)
=-6;??????
(2)3÷(-310)÷112
=(-10)×12
=-120;?????
(3)(-0.75)÷(-3)÷54
=(-34)×(-13)×45
=15.
23.
【解析】
根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
【解答】
解:由题意得,a+4=0,b-2=0,
解得a=-4,b=2,
所以,2a+3b-6=2×(-4)+3×2-6,
=-8+6-6,
=-8.
24.
【解析】
根据绝对值、相反数、倒数的概念和有理数的乘方、有理数的加法法则,求得:-|-5|的值,-3和0的相反数,-0.4的倒数,(-1)5,-2+72的值,然后将各个点标在数轴上.
【解答】
解:-|-5|=-5,-(-3)=3,-0.4的倒数是-2.5,0的相反数是0,(-1)5,=-1,-2+72=1.5,
在数轴上表示为:
25.
【解析】
任意两个数乘积的最大值.
任意两个数乘积的最大值.
【解答】
解:(1)选择卡片-7,-3,则-7×-3=21,21即为这5个数中,任意两个数乘积的最大值.
2选择卡片-7,1,则-7÷1=-7,-7即为这5个数中,任意两个数相除,商的最小值.
26.
【解析】
(1)利用非负数的性质即可列方程求得a和b的值;
(2)根据a和b的值,确定AB的长,然后利用旋转的性质求解;
(3)△MND扫过的面积是△MND的面积加上长是3cm和边长是MN的矩形的面积,据此即可求解.
【解答】
解:(1)根据题意得a-1=0且b-5=0,
解得a=1,b=5;
(2)落在x=b处的点是△ABC的顶点是B;
(3)△MND的面积是34,则△MND扫过的面积是1×3+34=12+34(cm2).
(满分120分;时间:120分钟)
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
?1. 下列说法中,正确的是(? ? ? ? )
A.任何实数的平方都是正数
B.正数的倒数必小于这个正数
C.绝对值等于它本身的数必是非负数
D.零除以任何一个实数都等于零
?
2. 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数.从轻重的角度看,最接近标准的工件是(? ? ? ? )
A.-2 B.-3 C.3 D.5
?
3. 下列计算正确的是(? ? ? ? )
A.18÷(-3)2=-2? B.-23÷(-3)3=827
C.(-213)3=-8127? D.-3-12×1=-212
?
4. 下列实数中,无理数是(? ? ??)
A.16 B.8 C.17 D.3.14159
?
5. 计算84÷(-7)等于( )
A.-12 B.12 C.-14 D.14
?
6. 有理数a,b在数轴上的位置如图,则a-b是(? ? ? ? )
A.正数 B.负数 C.零 D.无法确定
?7. 下列各数中无理数是( )
A.π2 B.227 C.4 D.327
?
8. 下列各数中,数值相等的有( )
①32和23;②-23与(-2)3;③23与(-2)3;④-22与(-2)2;⑤-(-3)与-|-3|;⑥425与1625;⑦(-1)2017与-1;⑧-(-0.1)3与-0.001
A.1组 B.2组 C.3组 D.4组
二、 填空题 (本题共计 12 小题 ,每题 3 分 ,共计36分 , ) ?
9. 数轴上表示-5的点离表示+3的点的距离是________个单位长度.
?
10. 在数轴上距原点3个单位长度的点表示的数是________.
?
11. 若|a+2|+(b-2)2=0,则ab=________.
?
12. 若m,n互为相反数,则m+n-1=________.
?
13. 如果a=8,b=-5,且ab>0,则a+b=_________.
?
14. 若x-1=|-3|,那么x=________.
?
15. 绝对值小于2的整数是________.
?
16. 若x2=4,|y|=3,且xy<0,则x-y的值为________.
?
17. 已知|a|=7,|b|=3,且a+b>0,则a=________.
?
18. 绝对值不大于2的所有整数和是________.
?
19. 小天上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况(单位:元):
星期
一
二
三
四
五
每股涨跌
+4
+4.5
-1
-2.5
-6
星期五收盘时每股是________元,本周内最高价每股________元.
?
20. 有13张红心扑克牌(上面的点数从1到13,为正数),和13张黑花扑克牌(上面的点数从1到13,为负数),任意打乱顺序后,从上面第一张(红心8)开始作为被减数,然后依次把后面点数逐一相减,最后得数是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. (-212)÷(-5)×(-313).
?
22. 计算.
(1)(-378)÷(-7)÷(-9);??????
(2)3÷(-310)÷112;?????
(3)(-0.75)÷(-3)÷54.
?
23. 若(a+4)2+(b-2)2=0,求?2a+3b-6的值.
?
24. 将下列各数在数轴上表示出来:-|-5|,-(-3),-0.4的倒数,0的相反数,(-1)5,比-2大72的数.
?
25. 如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
1从中取出2张卡片,使这两张卡片上数字的乘积最大,写出算式与这个最大值;
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,写出算式与这个最小值.
?
26. 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
(1)求a、b的值.
(2)落在x=b处的点是△ABC的哪个顶点?说明理由.
(3)小军测得△MND的边MN上的高为12cm,将△MND以每秒3cm的速度沿高的方向向上移动2秒,这时△MND扫过的面积是多少?
参考答案与试题解析
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.
【解析】
此题暂无解析
【解答】
解:对于A,由于0的平方是0,而不是正数,故A错误;
对于B,由于1的倒数是1,故B错误;
对于C,由绝对值的性质可知,绝对值等于它本身的数必是非负数,故C正确;
对于D,当除数为0时,没有意义,故D错误.
故选C.
2.
【解析】
根据正负数的意义,绝对值最小的即为最接近标准的.
【解答】
解:|-2|=2,|-3|=3,|3|=3,|5|=5,
∵ 2<3<5,
∴ 从轻重的角度来看,最接近标准的记录为-2.
故选A.
3.
【解析】
根据有理数的乘方,有理数的乘除法,有理数的减法运算,即可算出正确结果。
【解答】
解:A,18÷-32=18÷9=2,所以A计算错误;
B,-23÷-33=-8÷-27=827,所以B计算正确;
C,-2133=-733=-34327=-121927,所以C计算错误;
D,-3-12×1=-3-12=-312,所以D计算错误.
故选B.
4.
【解析】
此题暂无解析
【解答】
解:A,16=4,是有理数;
B,8=22,是无理数;
C,17是分数,所以是有理数;
D,3.14159是有限小数,所以是有理数,
故选B.
5.
【解析】
根据有理数的除法运算法则,得出结果.
【解答】
解:84÷(-7)=-12.
故选A.
6.
【解析】
首先根据a、b点所在位置判断正负,再根据有理数的减法法则可知a-b=a+(-b),然后根据有理数的加法法则可判断出结果的正负.
【解答】
解:∵ a在原点左边,
∴ a<0,
∵ b在原点右边,
∴ b>0,
∴ a-b=a+(-b)<0.
故选B.
7.
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】
A、π2是无理数,故A正确;
B、227是有理数,故B错误;
C、4=2是有理数,故C错误;
D、327=3是有理数,故D错误;
8.
【解析】
分别对每组数值进行计算,再作出判断即可.
【解答】
∵ 32=9,23=8;
-23=-8,(-2)3=-8;
23=8,(-2)3=-8
-22=-4,(-2)2=4;
-(-3)=3,-|-3|=-3;
425=165≠1625;
(-1)2017=-1;
-(-0.1)3=0.001≠-0.001.
∴ ①中两数的数值不相等;
②中两数的数值相等;
③中两数的数值不相等;
④中两数的数值不相等;
⑤中两数的数值不相等;
⑥中两数的数值不相等;
⑦中两数的数值相等;
⑧中两数的数值不相等.
∴ 数值相等的有②⑦共2组
二、 填空题 (本题共计 12 小题 ,每题 3 分 ,共计36分 )
9.
【解析】
根据数轴上点的意义可知数轴上表示-5的点与表+3的点的距离是|-5-3|=8.
【解答】
解:数轴上表示-5的点离表示+3的点的距离是|-5-3|=8个单位长度;
故答案为:8.
10.
【解析】
在数轴上,+3和-3到原点0的距离都等于3,据此进行填空即可.
【解答】
在数轴上距原点3个单位长度的点表示的数是±3.
11.
【解析】
根据非负数的性质进行计算即可.
【解答】
解:∵ |a+2|+(b-2)2=0,
∴ a+2=0,b-2=0,
∴ a=-2,b=2,
∴ ab=(-2)2=4.
故答案为:4.
12.
【解析】
根据互为相反数的两个数的和等于0可得m+n=0,然后代入计算即可得解.
【解答】
解:∵ m,n互为相反数,
∴ m+n=0,
∴ m+n-1=0-1=-1.
故答案为:-1.
13.
【解析】
首先根据a的绝对值是8,确定出a=±8,再根据b为负数,且ab>0,得到a为负数,最后代入计算即可.
【解答】
解:∵ |a|=8,
∴ a=±8.
∵ b=-5,ab>0,
∴ a=-8,b=-5,
∴ a+b=-8-5=-13.
故答案为:-13.
14.
【解析】
根据绝对值的性质得出两个一元一次方程,再解方程,即可解答.
【解答】
解:∵ x-1=-3,
∴ x-1=3,
∴ x-1=3或x-1=-3,
∴ x=4或x=-2.
故答案为:4或-2.
15.
【解析】
可以根据数轴得到答案,到原点距离小于2的整数只有三个:-1,1,0.
【解答】
解:绝对值小于2的整数是:-1,0,1.
16.
【解析】
首先根据乘方和绝对值的性质可得x=±2,y=±3,再由xy<0可得x、y异号,然后再计算出x-y的值.
【解答】
解:∵ x2=4,|y|=3,
∴ x=±2,y=±3,
∵ xy<0,
∴ ①x=2,y=-3,x-y=5;
②x=-2,y=3,x-y=-5,
故答案为:±5.
17.
【解析】
先由绝对值的定义求出a、b的可能值,再根据有理数的加法法则确定a与b的对应值.
【解答】
解:∵ |a|=7,|b|=3,
∴ a=7或-7,b=3或-3,
又∵ a+b>0,
∴ a=7,b=3或-3.
故答案为:7.
18.
【解析】
找出绝对值不大于2的所有整数,求出之和即可.
【解答】
解:绝对值不大于2的所有整数是-2,-1,0,1,2,
之和为-2-1+0+1+2=0,
故答案为:0.
19.
【解析】
根据表格求出星期五的股价;求出每天的股价即可做出判断.
【解答】
解:根据表格得:每天的股价分别为:28+4=32(元),32+4.5=36.5(元),36.5-1=35.5(元),35.5-2.5=33(元),33-6=27(元),
(1)星期五收盘时每股27元;
(2)星期二每股价格最高,为36.5元.
故答案为:(1)27;(2)36.5
20.
【解析】
根据互为相反数的两个数的和等于0判断出最后只有红心8减去黑化8,再根据减去一个数等于加上这个数的相反数进行计算即可得解.
【解答】
解:∵ 互为相反数的两个数的和等于0,
∴ 最后得数为8-(-8),
=8+8,
=16.
故答案为:16.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【解析】
把带分数化为假分数,然后根据有理数的乘法运算法则进行计算即可得解.
【解答】
解:(-212)÷(-5)×(-313),
=-52×15×103,
=-53.
22.
【解析】
(1)按照“两数相除,同号的正,异号得负,并把绝对值相除”的法则直接计算即可;
(2)把除法转化成乘法,再进行约分即可;
(3)先把小数转化成分数,再把除法转化成乘法,然后约分即可.
【解答】
解;(1)(-378)÷(-7)÷(-9)
=54÷(-9)
=-6;??????
(2)3÷(-310)÷112
=(-10)×12
=-120;?????
(3)(-0.75)÷(-3)÷54
=(-34)×(-13)×45
=15.
23.
【解析】
根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
【解答】
解:由题意得,a+4=0,b-2=0,
解得a=-4,b=2,
所以,2a+3b-6=2×(-4)+3×2-6,
=-8+6-6,
=-8.
24.
【解析】
根据绝对值、相反数、倒数的概念和有理数的乘方、有理数的加法法则,求得:-|-5|的值,-3和0的相反数,-0.4的倒数,(-1)5,-2+72的值,然后将各个点标在数轴上.
【解答】
解:-|-5|=-5,-(-3)=3,-0.4的倒数是-2.5,0的相反数是0,(-1)5,=-1,-2+72=1.5,
在数轴上表示为:
25.
【解析】
任意两个数乘积的最大值.
任意两个数乘积的最大值.
【解答】
解:(1)选择卡片-7,-3,则-7×-3=21,21即为这5个数中,任意两个数乘积的最大值.
2选择卡片-7,1,则-7÷1=-7,-7即为这5个数中,任意两个数相除,商的最小值.
26.
【解析】
(1)利用非负数的性质即可列方程求得a和b的值;
(2)根据a和b的值,确定AB的长,然后利用旋转的性质求解;
(3)△MND扫过的面积是△MND的面积加上长是3cm和边长是MN的矩形的面积,据此即可求解.
【解答】
解:(1)根据题意得a-1=0且b-5=0,
解得a=1,b=5;
(2)落在x=b处的点是△ABC的顶点是B;
(3)△MND的面积是34,则△MND扫过的面积是1×3+34=12+34(cm2).
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
