沪科版八年级数学上册第12章 一次函数 单元测试题(无答案)
文档属性
| 名称 | 沪科版八年级数学上册第12章 一次函数 单元测试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-03 00:00:00 | ||
图片预览

文档简介
沪科版八年级数学上册第12章
一次函数
单元测试题
姓名
班级
得分
一、选择题(每题3分,共30分)
1、下列函数(1),(2)
,(3)
,(4)
,(5)
中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2、一次函数y=2x﹣3的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3、如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
B.C.D.
4、直线y=﹣x+1上有两点A(x1,y1),B(x2,y2),且x1<x2,则y1与y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
5、已知一次函数y=kx-k,若y随着x的增大而减小,则该函数图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
6、在平面直角坐标系中,一次函数与坐标轴围成的三角形面积是:(
)
A、6
B、9
C、15
D、18
7、对于一次函数y=-2x+4,下列说法错误的是( )
A.函数值随自变量的增大而减小
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到y=2x的图象
D.函数的图象与x轴的交点坐标是(2,0)
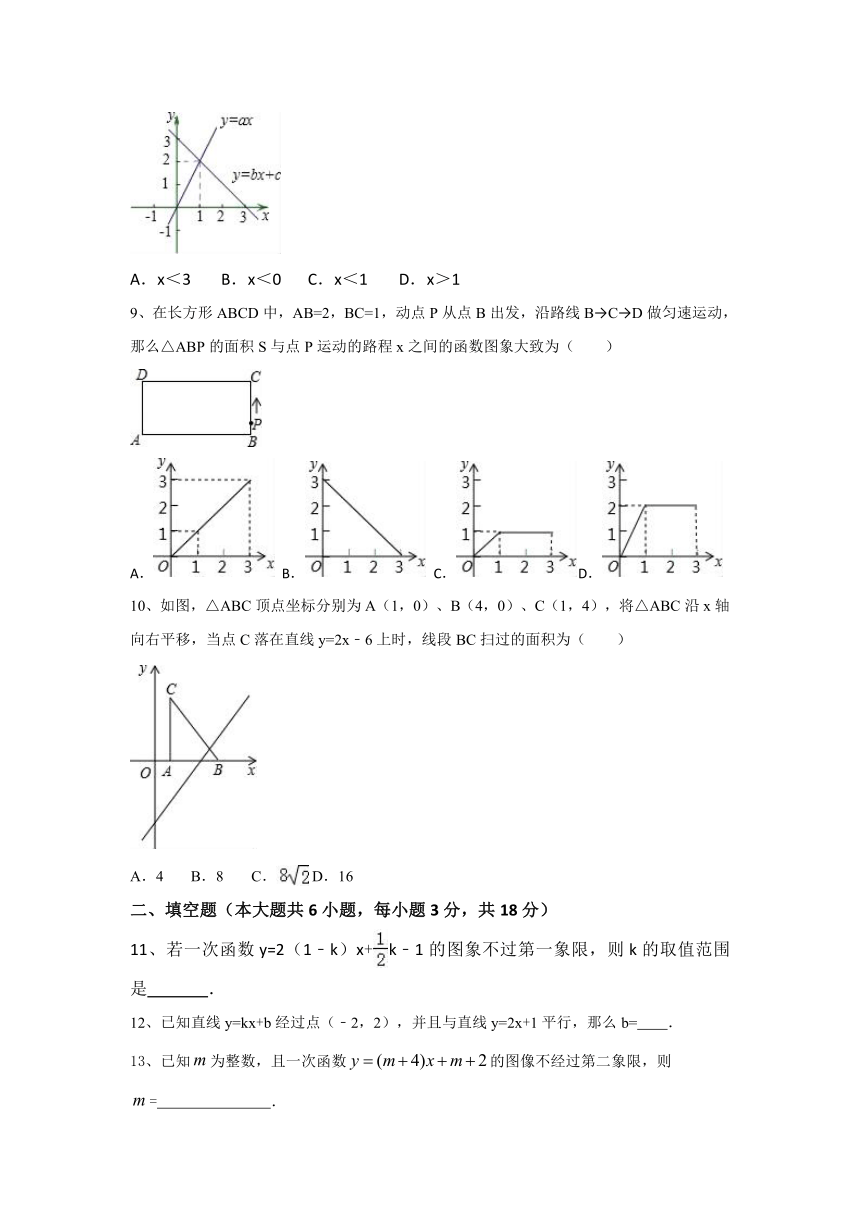
8、观察图中的函数图象,得关于x的不等式ax﹣bx<c的解集为( )
A.x<3
B.x<0
C.x<1
D.x>1
9、在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )
B.
C.D.
10、如图,△ABC顶点坐标分别为A(1,0)、B(4,0)、C(1,4),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为( )
A.4
B.8
C.
D.16
二、填空题(本大题共6小题,每小题3分,共18分)
11、若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是
.
12、已知直线y=kx+b经过点(﹣2,2),并且与直线y=2x+1平行,那么b= .
13、已知为整数,且一次函数的图像不经过第二象限,则=
.
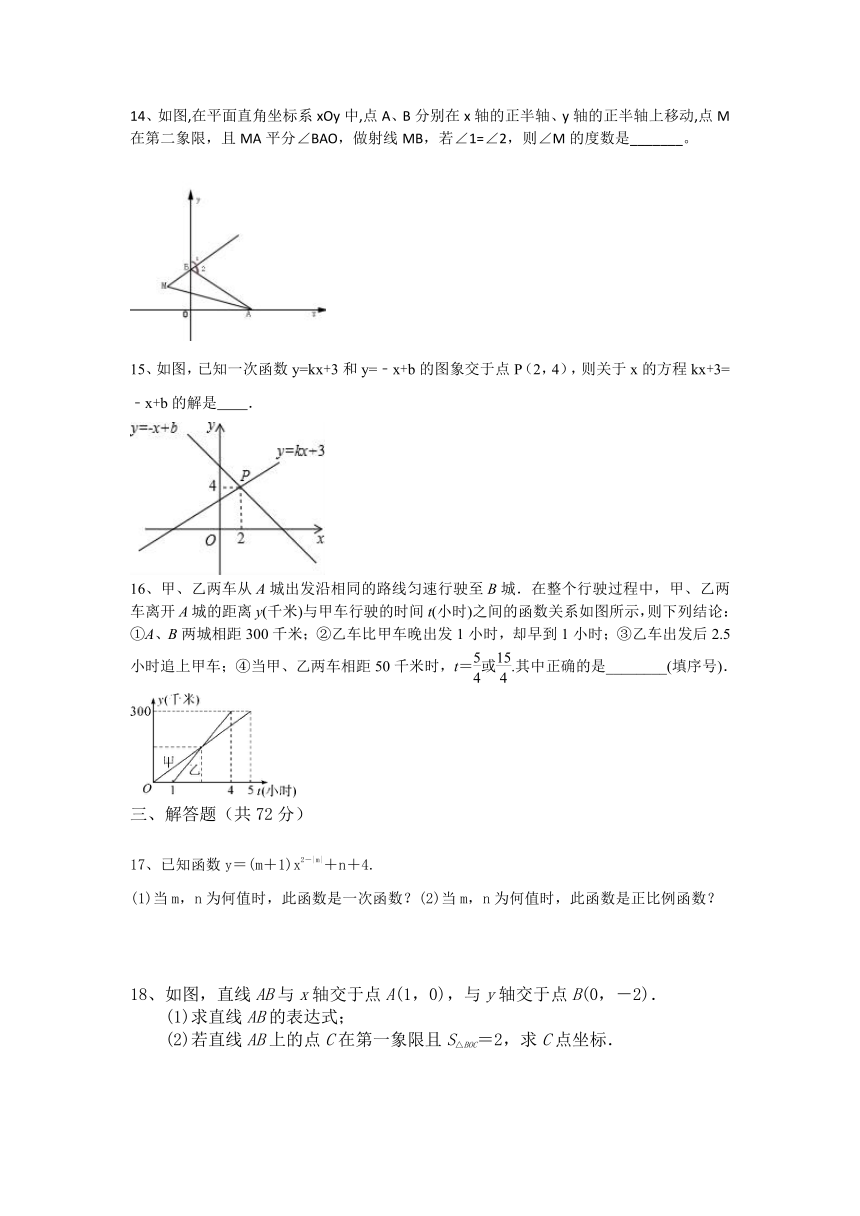
14、如图,在平面直角坐标系xOy中,点A、B分别在x轴的正半轴、y轴的正半轴上移动,点M在第二象限,且MA平分∠BAO,做射线MB,若∠1=∠2,则∠M的度数是_______。
15、如图,已知一次函数y=kx+3和y=﹣x+b的图象交于点P(2,4),则关于x的方程kx+3=﹣x+b的解是 .
16、甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的是________(填序号).
三、解答题(共72分)
17、已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?(2)当m,n为何值时,此函数是正比例函数?
18、如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的表达式;
(2)若直线AB上的点C在第一象限且S△BOC=2,求C点坐标.
19、如图,已知直线y=kx+b经过点A(5,0),B(1,4),直线y=2x-4与该直线交于点C.
(1)求直线AB的表达式;
(2)求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4≥kx+b的解集.
20、某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机
电冰箱
甲连锁店
200
170
乙连锁店
160
150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
21、已知直线经过(2,5),(﹣6,﹣7)两点
(1)求直线的函数解析式;
(2)若直线与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
22、如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两线的交点为P点,
(1)求△APB的面积;
(2)利用图象求当x取何值时,y1<y2.
23、如图,一只甲虫在5×5的方格如图,直线l1在平面直角坐标系中与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
24、某校八年级举行英语演讲比赛,派了两位老师去学校附近的超市购买笔记本作为奖品.经过了解得知,该超市的A,B两种笔记本的价格分别是12元和8元,他们准备购买这两种笔记本共30本.
(1)如果他们购买奖品共花费了300元,则这两种笔记本各买了多少本?
(2)两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量要不少于B种笔记本数量,但又不多于B种笔记本数量2倍,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
①请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
25、如图,直线的解析表达式为,且与轴交于点.直线经过点、,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一个点,使得与的面积相等,求点的坐标
一次函数
单元测试题
姓名
班级
得分
一、选择题(每题3分,共30分)
1、下列函数(1),(2)
,(3)
,(4)
,(5)
中,是一次函数的有(
)
A.4个
B.3个
C.2个
D.1个
2、一次函数y=2x﹣3的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3、如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
B.C.D.
4、直线y=﹣x+1上有两点A(x1,y1),B(x2,y2),且x1<x2,则y1与y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
5、已知一次函数y=kx-k,若y随着x的增大而减小,则该函数图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
6、在平面直角坐标系中,一次函数与坐标轴围成的三角形面积是:(
)
A、6
B、9
C、15
D、18
7、对于一次函数y=-2x+4,下列说法错误的是( )
A.函数值随自变量的增大而减小
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到y=2x的图象
D.函数的图象与x轴的交点坐标是(2,0)
8、观察图中的函数图象,得关于x的不等式ax﹣bx<c的解集为( )
A.x<3
B.x<0
C.x<1
D.x>1
9、在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )
B.
C.D.
10、如图,△ABC顶点坐标分别为A(1,0)、B(4,0)、C(1,4),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为( )
A.4
B.8
C.
D.16
二、填空题(本大题共6小题,每小题3分,共18分)
11、若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是
.
12、已知直线y=kx+b经过点(﹣2,2),并且与直线y=2x+1平行,那么b= .
13、已知为整数,且一次函数的图像不经过第二象限,则=
.
14、如图,在平面直角坐标系xOy中,点A、B分别在x轴的正半轴、y轴的正半轴上移动,点M在第二象限,且MA平分∠BAO,做射线MB,若∠1=∠2,则∠M的度数是_______。
15、如图,已知一次函数y=kx+3和y=﹣x+b的图象交于点P(2,4),则关于x的方程kx+3=﹣x+b的解是 .
16、甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的是________(填序号).
三、解答题(共72分)
17、已知函数y=(m+1)x2-|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?(2)当m,n为何值时,此函数是正比例函数?
18、如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的表达式;
(2)若直线AB上的点C在第一象限且S△BOC=2,求C点坐标.
19、如图,已知直线y=kx+b经过点A(5,0),B(1,4),直线y=2x-4与该直线交于点C.
(1)求直线AB的表达式;
(2)求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4≥kx+b的解集.
20、某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
空调机
电冰箱
甲连锁店
200
170
乙连锁店
160
150
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
21、已知直线经过(2,5),(﹣6,﹣7)两点
(1)求直线的函数解析式;
(2)若直线与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
22、如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两线的交点为P点,
(1)求△APB的面积;
(2)利用图象求当x取何值时,y1<y2.
23、如图,一只甲虫在5×5的方格如图,直线l1在平面直角坐标系中与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
24、某校八年级举行英语演讲比赛,派了两位老师去学校附近的超市购买笔记本作为奖品.经过了解得知,该超市的A,B两种笔记本的价格分别是12元和8元,他们准备购买这两种笔记本共30本.
(1)如果他们购买奖品共花费了300元,则这两种笔记本各买了多少本?
(2)两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量要不少于B种笔记本数量,但又不多于B种笔记本数量2倍,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
①请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
25、如图,直线的解析表达式为,且与轴交于点.直线经过点、,直线,交于点.
(1)求点的坐标;
(2)求直线的解析表达式;
(3)求的面积;
(4)在直线上存在异于点的另一个点,使得与的面积相等,求点的坐标
