人教版八年级上册13.3.2.1等边三角形的性质与判定学案(表格式 无答案)
文档属性
| 名称 | 人教版八年级上册13.3.2.1等边三角形的性质与判定学案(表格式 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 20:07:57 | ||
图片预览

文档简介
导学提纲
课题
13.3.2.1三角形的性质与判定
主备人
课型
新授课
课时安排
1
总课时数
1
上课日期
教·学目标
1.探索等边三角形的性质和判定.2.能运用等边三角形的性质和判定进行计算和证明.
教·学重难点
重点:
探索等边三角形的性质和判定.难点:能运用等边三角形的性质和判定进行计算和证明.
教·学过程
札记
导小明想制作一个三角形的相框,他有四根木条长度分别为10cm,10cm,10cm,6cm,你能帮他设计出几种形状的三角形?如果三角形的底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.二.思问题1
等边三角形的三个内角之间有什么关系?问题2
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
图形等腰三角形等边三角形性质两条边相等两个底角相等底边上的中线、高和顶角的平分线互相重合对称轴(1条)例1
如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.例2
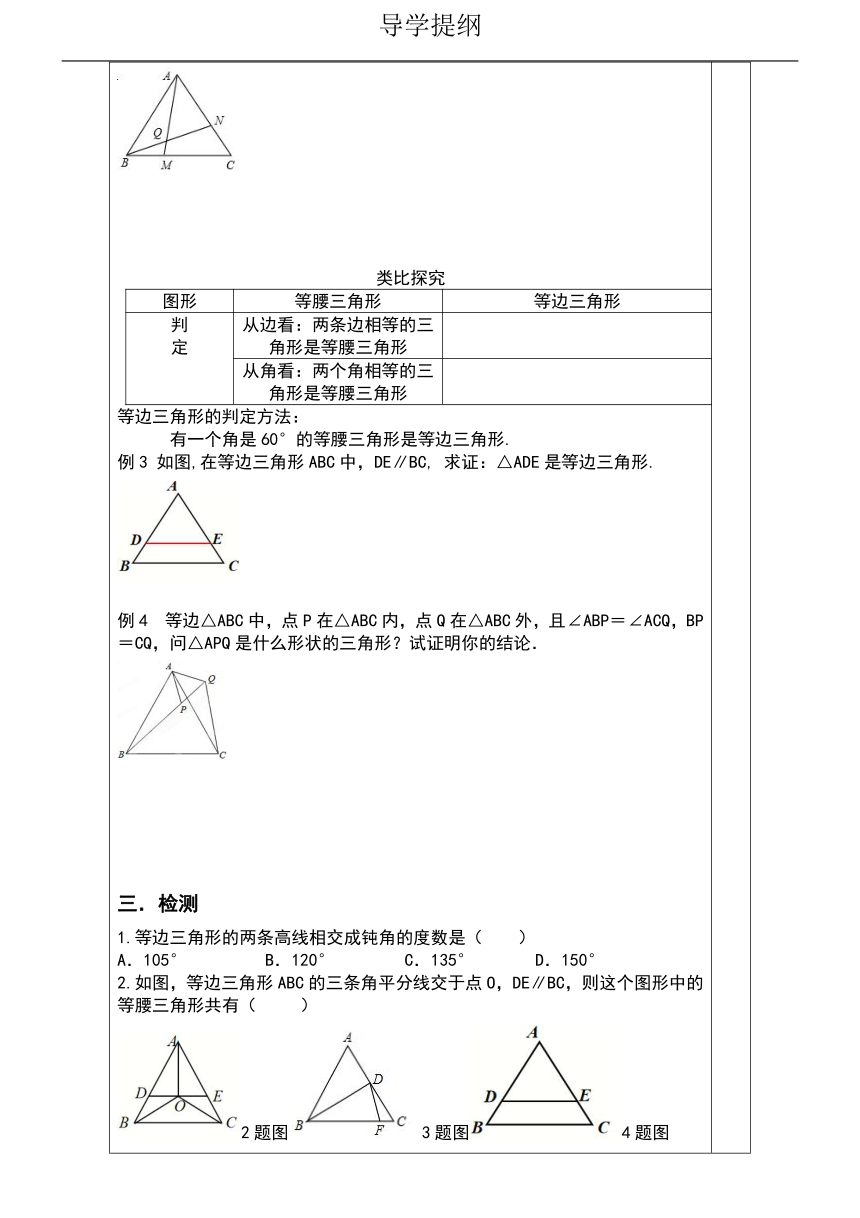
△ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?类比探究图形等腰三角形等边三角形判定从边看:两条边相等的三角形是等腰三角形从角看:两个角相等的三角形是等腰三角形等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.例3
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.例4
等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.三.检测1.等边三角形的两条高线相交成钝角的度数是( )A.105°
B.120°
C.135°
D.150°
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)2题图3题图4题图3.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )A.10°
B.15°
C.20°
D.25°
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC
=2cm,则△ADE的周长是
cm.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.求证:△AEF≌△BEC.6.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
拓展提升:7.图①、图②中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图①,线段AN与线段BM是否相等?请说明理由;(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.四、课堂小结、形成网络小结与网络
(二)反思
课题
13.3.2.1三角形的性质与判定
主备人
课型
新授课
课时安排
1
总课时数
1
上课日期
教·学目标
1.探索等边三角形的性质和判定.2.能运用等边三角形的性质和判定进行计算和证明.
教·学重难点
重点:
探索等边三角形的性质和判定.难点:能运用等边三角形的性质和判定进行计算和证明.
教·学过程
札记
导小明想制作一个三角形的相框,他有四根木条长度分别为10cm,10cm,10cm,6cm,你能帮他设计出几种形状的三角形?如果三角形的底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫作等边三角形.二.思问题1
等边三角形的三个内角之间有什么关系?问题2
等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
图形等腰三角形等边三角形性质两条边相等两个底角相等底边上的中线、高和顶角的平分线互相重合对称轴(1条)例1
如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.例2
△ABC为正三角形,点M是BC边上任意一点,点N是CA边上任意一点,且BM=CN,BN与AM相交于Q点,∠BQM等于多少度?类比探究图形等腰三角形等边三角形判定从边看:两条边相等的三角形是等腰三角形从角看:两个角相等的三角形是等腰三角形等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.例3
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.例4
等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.三.检测1.等边三角形的两条高线相交成钝角的度数是( )A.105°
B.120°
C.135°
D.150°
2.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有(
)2题图3题图4题图3.在等边△ABC中,BD平分∠ABC,BD=BF,则∠CDF的度数是( )A.10°
B.15°
C.20°
D.25°
如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC
=2cm,则△ADE的周长是
cm.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.求证:△AEF≌△BEC.6.如图,A、O、D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
拓展提升:7.图①、图②中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图①,线段AN与线段BM是否相等?请说明理由;(2)如图②,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.四、课堂小结、形成网络小结与网络
(二)反思
