人教版数学九年级上册 24.1 圆的有关性质 同步训练习题(word含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.1 圆的有关性质 同步训练习题(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 11:26:47 | ||
图片预览


文档简介
人教版
九年级上册
24.1
圆的有关性质
同步训练
一、选择题
1.
下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为
( )
A.1
B.2
C.3
D.4
2.
如图,四边形ABCD是半圆的内接四边形,AB是直径,=.若∠C=110°,则∠ABC的度数等于
( )
A.55°
B.60°
C.65°
D.70°
3.
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=59°,则∠C等于( )
A.29°
B.31°
C.59°
D.62°
4.
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.
5
B.
7
C.
9
D.
11
5.
如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
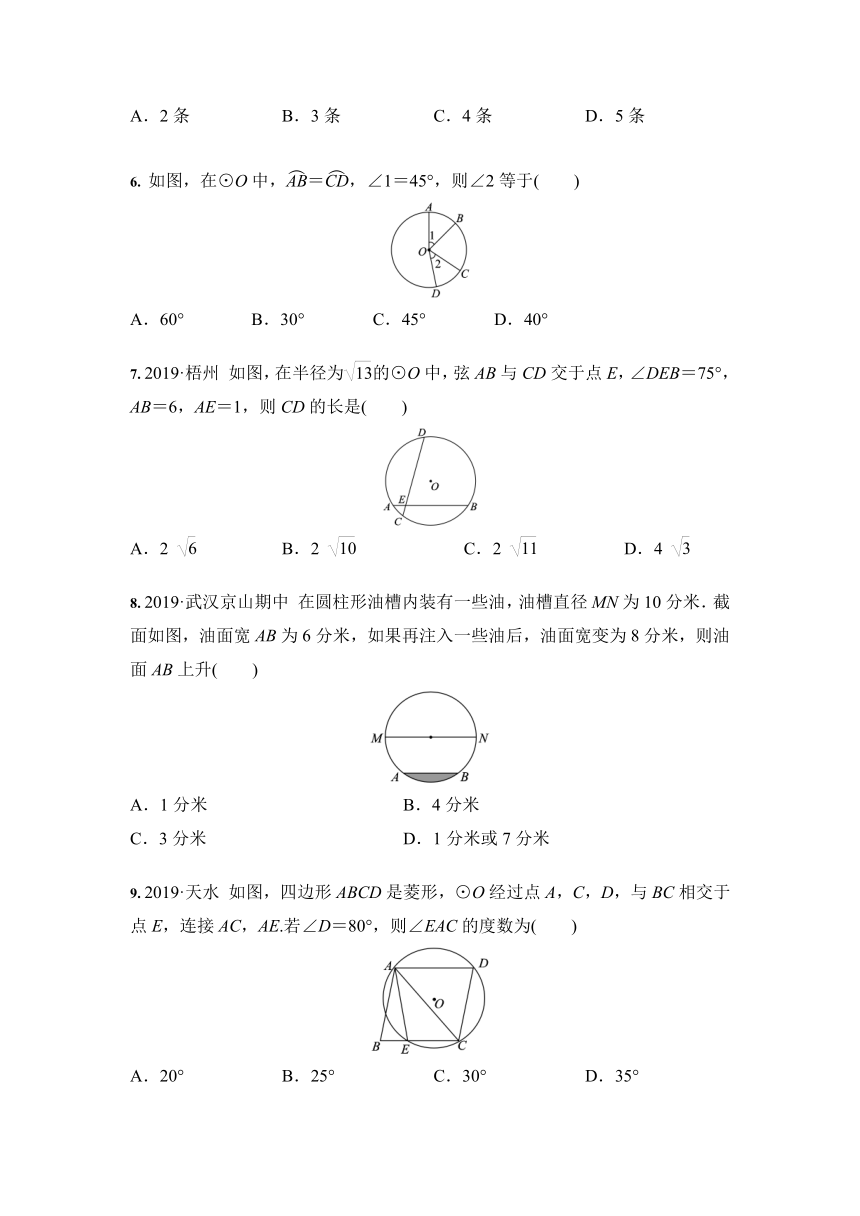
A.2条
B.3条
C.4条
D.5条
6.
如图,在⊙O中,=,∠1=45°,则∠2等于( )
A.60°
B.30°
C.45°
D.40°
7.
2019·梧州
如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2
B.2
C.2
D.4
8.
2019·武汉京山期中
在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,油面宽变为8分米,则油面AB上升( )
A.1分米
B.4分米
C.3分米
D.1分米或7分米
9.
2019·天水
如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为( )
A.20°
B.25°
C.30°
D.35°
10.
如图,量角器的零刻度线与三角尺ABC的斜边AB重合,其中量角器的零刻度线的端点N与点A重合,射线CP从CA处出发按顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是( )
A.48°
B.64°
C.96°
D.132°
二、填空题
11.
如图所示,AB是☉O的直径,弦CD⊥AB于H,∠A=30°,CD=2,则☉O的半径是 .?
12.
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
13.
如图,一下水管道横截面为圆形,直径为100
cm,下雨前水面宽为60
cm,一场大雨过后,水面宽为80
cm,则水位上升了 cm.?
14.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=________.
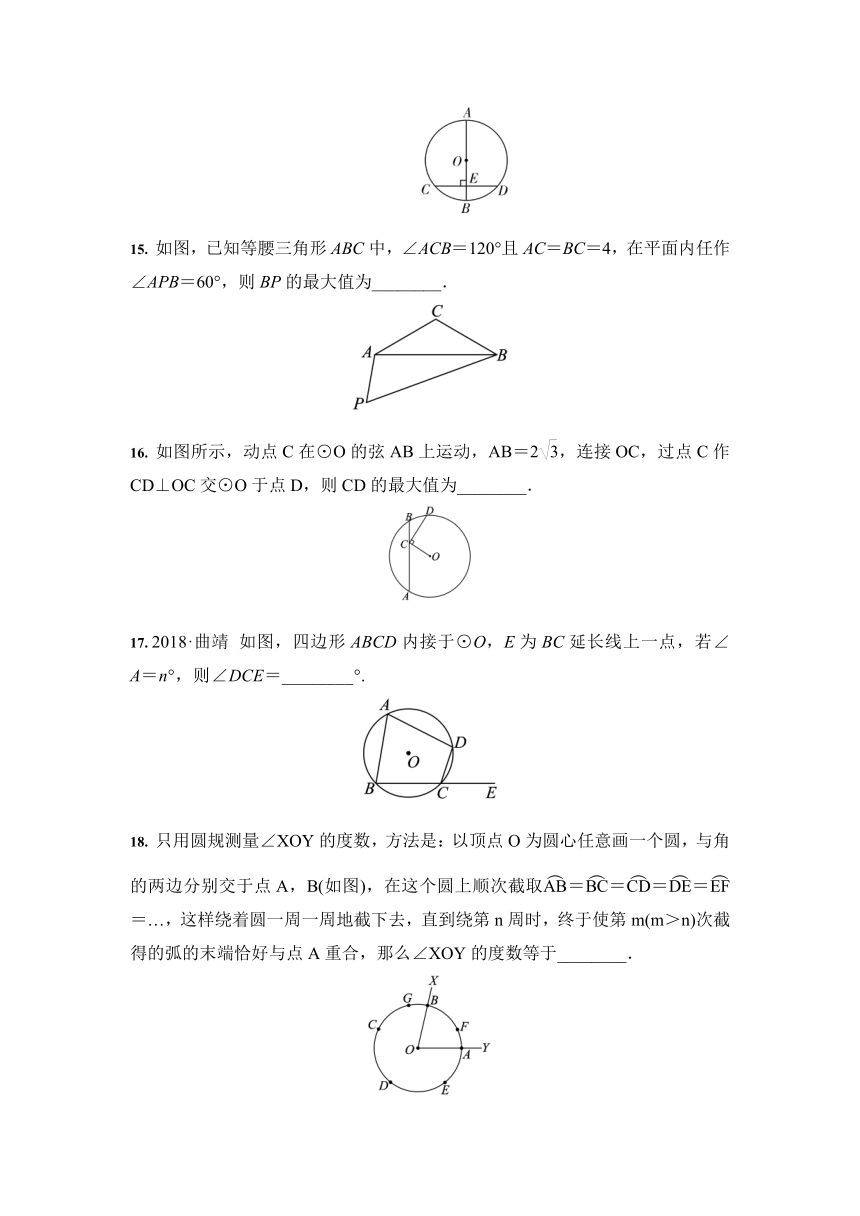
15.
如图,已知等腰三角形ABC中,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,则BP的最大值为________.
16.
如图所示,动点C在⊙O的弦AB上运动,AB=2,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
17.
2018·曲靖
如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE=________°.
18.
只用圆规测量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图),在这个圆上顺次截取=====…,这样绕着圆一周一周地截下去,直到绕第n周时,终于使第m(m>n)次截得的弧的末端恰好与点A重合,那么∠XOY的度数等于________.
三、解答题
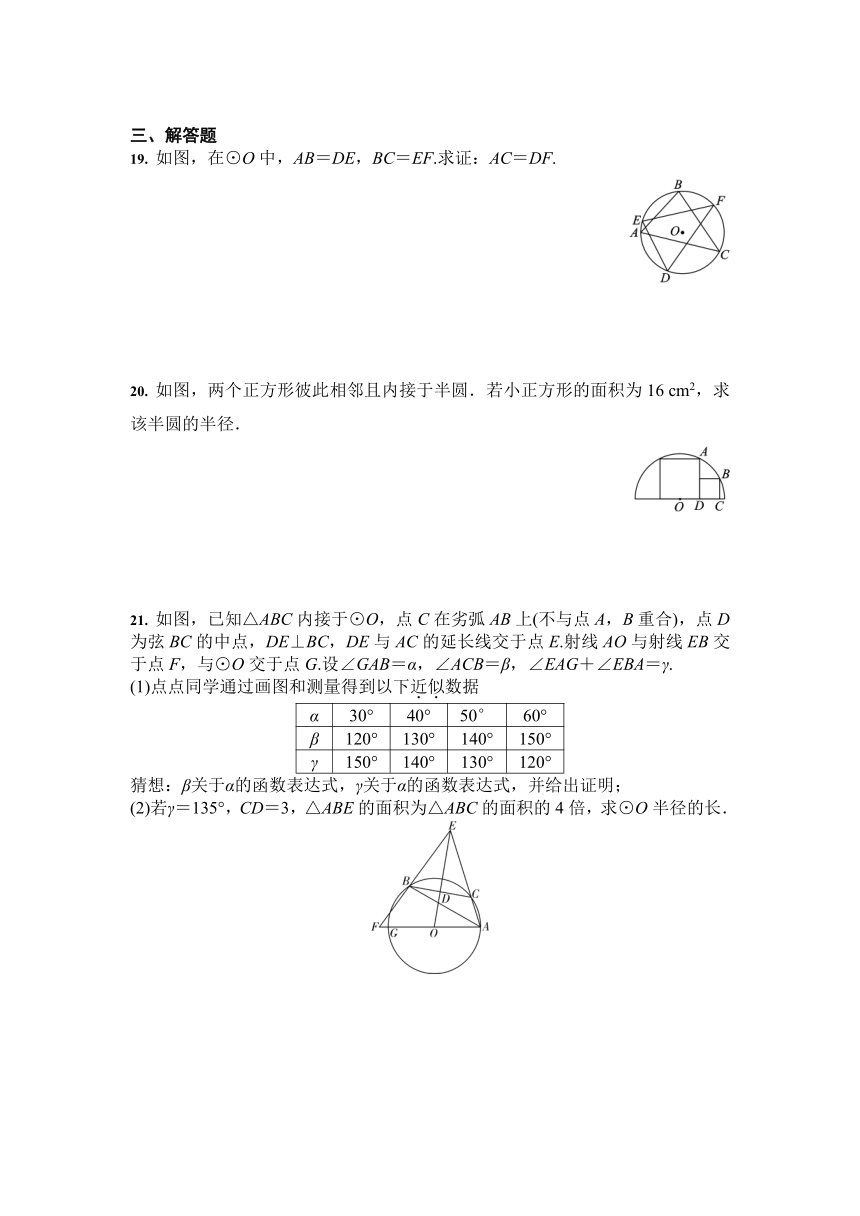
19.
如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
20.
如图,两个正方形彼此相邻且内接于半圆.若小正方形的面积为16
cm2,求该半圆的半径.
21.
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E.射线AO与射线EB交于点F,与⊙O交于点G.设∠GAB=α,∠ACB=β,∠EAG+∠EBA=γ.
(1)点点同学通过画图和测量得到以下近似数据
α
30°
40°
50°
60°
β
120°
130°
140°
150°
γ
150°
140°
130°
120°
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
22.
如图,四边形OBCD中的三个顶点在⊙O上,A是优弧BAD上的一个动点(不与点B,D重合).
(1)当圆心O在∠BAD的内部时,若∠BOD=120°,则∠OBA+∠ODA=________°.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
人教版
九年级上册
24.1
圆的有关性质
同步训练-答案
一、选择题
1.
【答案】C
2.
【答案】A ∵=,∴∠CAB=∠DAB=35°.
∵AB是直径,∴∠ACB=90°,
∴∠ABC=90°-∠CAB=55°,故选A.
3.
【答案】B
4.
【答案】A
5.
【答案】B
6.
【答案】C
7.
【答案】C
8.
【答案】D
9.
【答案】C
10.
【答案】C
二、填空题
11.
【答案】2 ∴∠A=∠ACO=30°,∴∠COH=60°.
∵OB⊥CD,CD=2,∴CH=,∴OH=1,
∴OC=2.
12.
【答案】50°
13.
【答案】10或70
由垂径定理得:BC=AB=30
cm.
在Rt△OBC中,OC==40(cm).
当水位上升到圆心以下且水面宽80
cm时,
圆心到水面距离==30(cm),
水面上升的高度为:40-30=10(cm).
当水位上升到圆心以上且水面宽80
cm时,水面上升的高度为:40+30=70(cm).
综上可得,水面上升的高度为10
cm或70
cm.
故答案为10或70.
14.
【答案】
4-
15.
【答案】8
16.
【答案】
17.
【答案】n
18.
【答案】°
三、解答题
19.
【答案】
证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
20.
【答案】
解:如图,连接OA,OB.
根据正方形的面积公式可得小正方形的边长为4
cm.
设大正方形的边长为x
cm,则OD=x
cm.
根据勾股定理,得OA2=OD2+AD2,OB2=OC2+BC2.
又∵OA=OB,
∴(x)2+x2=(x+4)2+42,
解得x1=8,x2=-4(不符合题意,舍去),
∴大正方形的边长为8
cm,OD=4
cm,
∴OA2=OD2+AD2=42+82=80,
∴OA==4
(cm).
故该半圆的半径为4
cm.
21.
【答案】
【思维教练】(1)观察表格可猜想β=90°+α,γ=180°-α.连接BG,由直径所对的圆周角为90°和圆内接四边形的对角和为180°即可得出β=90°+α;由题干条件易知△EBD≌△EGD,∠EBC=∠ECB,再由三角形的外角和定理和β=90°+α,利用角度之间的转化即可得出结论;(2)由(1)的结论可以得出α=∠BAG=45°,β=∠ACB=135°,∴∠ECB=45°,∠CEB=90°,△ECD、△BEC、△ABG都是等腰直角三角形,由CD的长,可得出BE和CE的长,再由题干条件△ABE的面积是△ABC的面积的4倍可得出AC的长,利用勾股定理在△ABE中求出AB的长,再利用勾股定理在△ABG求出AG的长,即可求出半径长.
①
(1)①β=90°+α,γ=180°-α
证明:如解图①,连接BG,
∵AG是⊙O的直径,∴∠ABG=90°,
∴α+∠BGA=90°,(1分)
又∵四边形ACBG内接于⊙O,
∴β+∠BGA=180°,
∴β-α=90°,
即β=90°+α;(3分)
②∵D是BC的中点,且DE⊥BC,
∴△EBD≌△ECD,∴∠EBC=∠ECB,
∵∠EAG+∠EBA=γ,
∴∠EAB+α+∠EBC+∠CBA=γ,
∵∠EAB+∠CBA=∠ECB,
∴2∠ECB+α=γ,(4分)
∴2(180°-β
)+α=γ,
由①β=90°+α代入后化简得,γ=180°-α;(6分)
(2)如解图②,连接BG,
②
∵γ=135°,γ=180°-α,
∴α=45°,β=135°,
∴∠AGB=∠ECB=45°,(8分)
∴△ECD和△ABG都是等腰直角三角形,
又∵△ABE的面积是△ABC的面积的4倍,
∴AE=4AC,∴EC=3AC,(9分)
∵CD=3,∴CE=3,AC=,∴AE=4,(10分)
∵∠BEA=90°,
∴由勾股定理得,AB====5,(11分)
∴AG=AB=×5=10,
∴r=5.(12分)
22.
【答案】
解:(1)60
(2)①如图(a).
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC.
又∵∠BAD+∠BCD=180°,∠BAD=∠BOD,
∴∠BOD+∠BOD=180°,解得∠BOD=120°,∴∠BAD=∠BOD=×120°=60°,∠OBC=∠ODC=180°-∠BOD=180°-120°=60°.
又∵∠ABC+∠ADC=180°,
∴∠OBA+∠ODA=∠ABC+∠ADC-(∠OBC+∠ODC)=180°-(60°+60°)=60°.
②如图(b)所示,连接AO.
∵OA=OB,
∴∠OBA=∠OAB.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAB=∠OAD+∠BAD,
∴∠OBA=∠ODA+∠BAD=∠ODA+60°.
如图(c),同理可得∠ODA=∠OBA+60°.
九年级上册
24.1
圆的有关性质
同步训练
一、选择题
1.
下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为
( )
A.1
B.2
C.3
D.4
2.
如图,四边形ABCD是半圆的内接四边形,AB是直径,=.若∠C=110°,则∠ABC的度数等于
( )
A.55°
B.60°
C.65°
D.70°
3.
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=59°,则∠C等于( )
A.29°
B.31°
C.59°
D.62°
4.
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
A.
5
B.
7
C.
9
D.
11
5.
如图,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条
B.3条
C.4条
D.5条
6.
如图,在⊙O中,=,∠1=45°,则∠2等于( )
A.60°
B.30°
C.45°
D.40°
7.
2019·梧州
如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
A.2
B.2
C.2
D.4
8.
2019·武汉京山期中
在圆柱形油槽内装有一些油,油槽直径MN为10分米.截面如图,油面宽AB为6分米,如果再注入一些油后,油面宽变为8分米,则油面AB上升( )
A.1分米
B.4分米
C.3分米
D.1分米或7分米
9.
2019·天水
如图,四边形ABCD是菱形,⊙O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为( )
A.20°
B.25°
C.30°
D.35°
10.
如图,量角器的零刻度线与三角尺ABC的斜边AB重合,其中量角器的零刻度线的端点N与点A重合,射线CP从CA处出发按顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是( )
A.48°
B.64°
C.96°
D.132°
二、填空题
11.
如图所示,AB是☉O的直径,弦CD⊥AB于H,∠A=30°,CD=2,则☉O的半径是 .?
12.
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=________.
13.
如图,一下水管道横截面为圆形,直径为100
cm,下雨前水面宽为60
cm,一场大雨过后,水面宽为80
cm,则水位上升了 cm.?
14.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=________.
15.
如图,已知等腰三角形ABC中,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,则BP的最大值为________.
16.
如图所示,动点C在⊙O的弦AB上运动,AB=2,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
17.
2018·曲靖
如图,四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE=________°.
18.
只用圆规测量∠XOY的度数,方法是:以顶点O为圆心任意画一个圆,与角的两边分别交于点A,B(如图),在这个圆上顺次截取=====…,这样绕着圆一周一周地截下去,直到绕第n周时,终于使第m(m>n)次截得的弧的末端恰好与点A重合,那么∠XOY的度数等于________.
三、解答题
19.
如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
20.
如图,两个正方形彼此相邻且内接于半圆.若小正方形的面积为16
cm2,求该半圆的半径.
21.
如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E.射线AO与射线EB交于点F,与⊙O交于点G.设∠GAB=α,∠ACB=β,∠EAG+∠EBA=γ.
(1)点点同学通过画图和测量得到以下近似数据
α
30°
40°
50°
60°
β
120°
130°
140°
150°
γ
150°
140°
130°
120°
猜想:β关于α的函数表达式,γ关于α的函数表达式,并给出证明;
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
22.
如图,四边形OBCD中的三个顶点在⊙O上,A是优弧BAD上的一个动点(不与点B,D重合).
(1)当圆心O在∠BAD的内部时,若∠BOD=120°,则∠OBA+∠ODA=________°.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
人教版
九年级上册
24.1
圆的有关性质
同步训练-答案
一、选择题
1.
【答案】C
2.
【答案】A ∵=,∴∠CAB=∠DAB=35°.
∵AB是直径,∴∠ACB=90°,
∴∠ABC=90°-∠CAB=55°,故选A.
3.
【答案】B
4.
【答案】A
5.
【答案】B
6.
【答案】C
7.
【答案】C
8.
【答案】D
9.
【答案】C
10.
【答案】C
二、填空题
11.
【答案】2 ∴∠A=∠ACO=30°,∴∠COH=60°.
∵OB⊥CD,CD=2,∴CH=,∴OH=1,
∴OC=2.
12.
【答案】50°
13.
【答案】10或70
由垂径定理得:BC=AB=30
cm.
在Rt△OBC中,OC==40(cm).
当水位上升到圆心以下且水面宽80
cm时,
圆心到水面距离==30(cm),
水面上升的高度为:40-30=10(cm).
当水位上升到圆心以上且水面宽80
cm时,水面上升的高度为:40+30=70(cm).
综上可得,水面上升的高度为10
cm或70
cm.
故答案为10或70.
14.
【答案】
4-
15.
【答案】8
16.
【答案】
17.
【答案】n
18.
【答案】°
三、解答题
19.
【答案】
证明:∵AB=DE,BC=EF,
∴=,=,
∴+=+,
∴=,∴AC=DF.
20.
【答案】
解:如图,连接OA,OB.
根据正方形的面积公式可得小正方形的边长为4
cm.
设大正方形的边长为x
cm,则OD=x
cm.
根据勾股定理,得OA2=OD2+AD2,OB2=OC2+BC2.
又∵OA=OB,
∴(x)2+x2=(x+4)2+42,
解得x1=8,x2=-4(不符合题意,舍去),
∴大正方形的边长为8
cm,OD=4
cm,
∴OA2=OD2+AD2=42+82=80,
∴OA==4
(cm).
故该半圆的半径为4
cm.
21.
【答案】
【思维教练】(1)观察表格可猜想β=90°+α,γ=180°-α.连接BG,由直径所对的圆周角为90°和圆内接四边形的对角和为180°即可得出β=90°+α;由题干条件易知△EBD≌△EGD,∠EBC=∠ECB,再由三角形的外角和定理和β=90°+α,利用角度之间的转化即可得出结论;(2)由(1)的结论可以得出α=∠BAG=45°,β=∠ACB=135°,∴∠ECB=45°,∠CEB=90°,△ECD、△BEC、△ABG都是等腰直角三角形,由CD的长,可得出BE和CE的长,再由题干条件△ABE的面积是△ABC的面积的4倍可得出AC的长,利用勾股定理在△ABE中求出AB的长,再利用勾股定理在△ABG求出AG的长,即可求出半径长.
①
(1)①β=90°+α,γ=180°-α
证明:如解图①,连接BG,
∵AG是⊙O的直径,∴∠ABG=90°,
∴α+∠BGA=90°,(1分)
又∵四边形ACBG内接于⊙O,
∴β+∠BGA=180°,
∴β-α=90°,
即β=90°+α;(3分)
②∵D是BC的中点,且DE⊥BC,
∴△EBD≌△ECD,∴∠EBC=∠ECB,
∵∠EAG+∠EBA=γ,
∴∠EAB+α+∠EBC+∠CBA=γ,
∵∠EAB+∠CBA=∠ECB,
∴2∠ECB+α=γ,(4分)
∴2(180°-β
)+α=γ,
由①β=90°+α代入后化简得,γ=180°-α;(6分)
(2)如解图②,连接BG,
②
∵γ=135°,γ=180°-α,
∴α=45°,β=135°,
∴∠AGB=∠ECB=45°,(8分)
∴△ECD和△ABG都是等腰直角三角形,
又∵△ABE的面积是△ABC的面积的4倍,
∴AE=4AC,∴EC=3AC,(9分)
∵CD=3,∴CE=3,AC=,∴AE=4,(10分)
∵∠BEA=90°,
∴由勾股定理得,AB====5,(11分)
∴AG=AB=×5=10,
∴r=5.(12分)
22.
【答案】
解:(1)60
(2)①如图(a).
∵四边形OBCD为平行四边形,
∴∠BOD=∠BCD,∠OBC=∠ODC.
又∵∠BAD+∠BCD=180°,∠BAD=∠BOD,
∴∠BOD+∠BOD=180°,解得∠BOD=120°,∴∠BAD=∠BOD=×120°=60°,∠OBC=∠ODC=180°-∠BOD=180°-120°=60°.
又∵∠ABC+∠ADC=180°,
∴∠OBA+∠ODA=∠ABC+∠ADC-(∠OBC+∠ODC)=180°-(60°+60°)=60°.
②如图(b)所示,连接AO.
∵OA=OB,
∴∠OBA=∠OAB.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAB=∠OAD+∠BAD,
∴∠OBA=∠ODA+∠BAD=∠ODA+60°.
如图(c),同理可得∠ODA=∠OBA+60°.
同课章节目录
