人教版七年级数学上册1.2.2数轴课件(32张)
文档属性
| 名称 | 人教版七年级数学上册1.2.2数轴课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 637.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 07:12:35 | ||
图片预览








文档简介
(共32张PPT)
1.2.2
数
轴
义务教育课程标准实验教科书
数学
七年级
上册
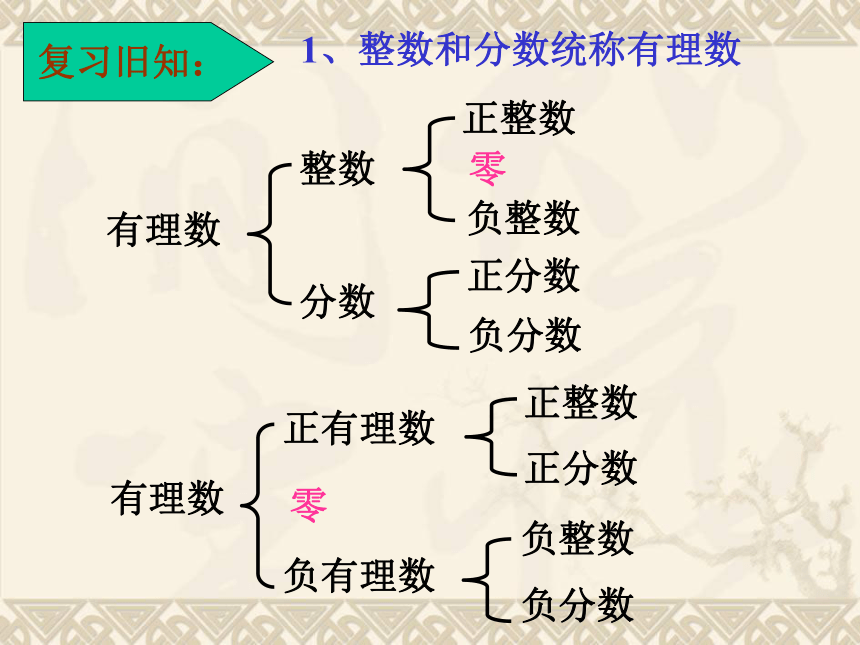
1、整数和分数统称有理数
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
复习旧知:
把下列各数填在相应的集合中:
正数集合:{
};
负数集合:{
};
分数集合:{
};
整数集合:{
};
非负数集合:{
};
有理数集合:{
};
复习旧知:
℃
℃
℃
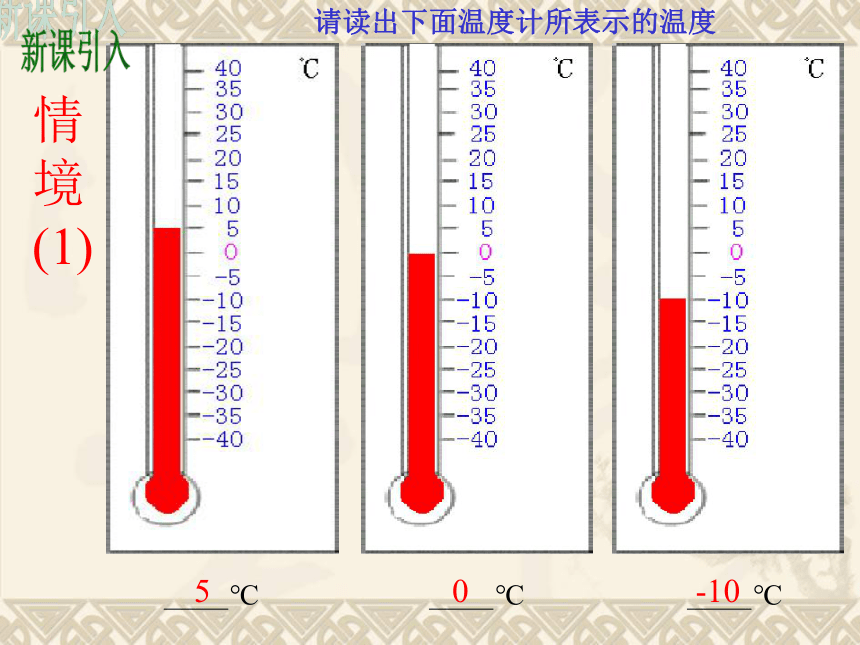
5
0
-10
请读出下面温度计所表示的温度
新课引入
情境(1)
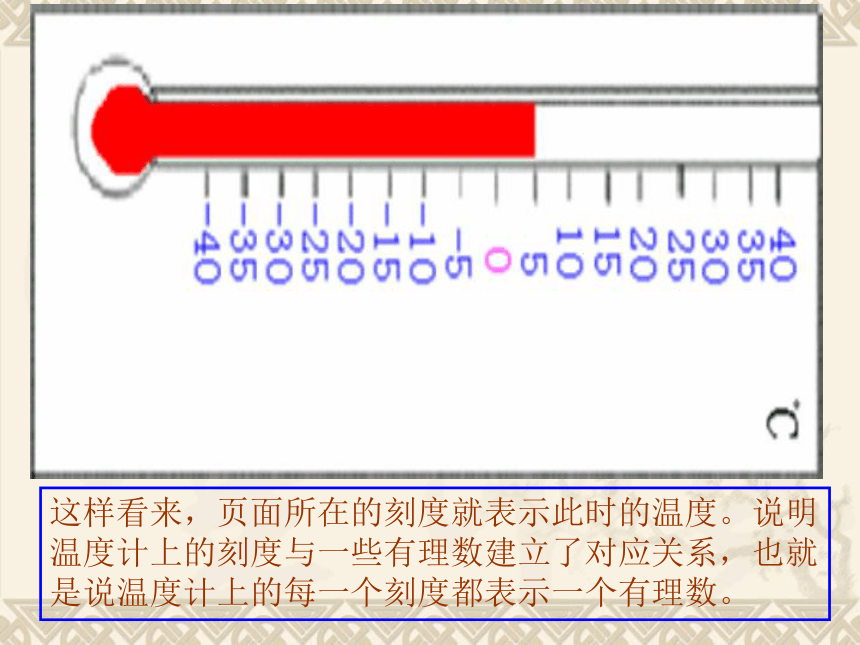
这样看来,页面所在的刻度就表示此时的温度。说明温度计上的刻度与一些有理数建立了对应关系,也就是说温度计上的每一个刻度都表示一个有理数。
1、怎样用数简明地表示这些树、电线杆与汽车站的相对位置关系?
情境2:
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆。你能用图示的方法表示这一情境吗?
方向和距离
2、生活中还有这种例子吗?请举手列举出来。
3、我们能否利用一个类似于温度计的图形,用它的刻度来表示所有的有理数呢?这就是我们今天一起研究的—数轴。
情境2:
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆。你能用图示的方法表示这一情境吗?
1、观察温度计的刻度规律,你能发现什么?
刻度有正、有负,也有0。
2、类比温度计,你能画图完成上面我们的问题吗?
(1)马路可以用什么几何图形代表?
(2)你认为站牌起什么作用?
(3)你是怎样确定问题中各物体的位置的?
直线
基准点
方向,与站牌的距离
O
0
1
3
7.5
-3
-4.8
探究
1.0代表什么?
2.数的符号的实际意义是什么?
3.如下图,在一条直线上,A,B的距离等于B,C的距离,点B表示3,点C能表示7.5吗?为什么?
4.上述方法表示了这些树、电线杆与汽车站的相对位置关系。例如,-4.8表示位于汽车站西侧4.8米处的电线杆。你能再举个例子吗?
0
1
3
7.5
-3
-4.8
B
A
O
E
C
D
操作与归纳
一般地,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线就叫做“数轴”。
1、画一条水平(或竖直)直线,在直线上任取一点表示数0,这个点做叫原点。
2、通常规定直线上从原点向右(或上)的方向为正方向,从原点向左(或下)的方向为负方向。
3、选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,···;从原点向左,用类似方法依次表示1,2,3,···,就得到了数轴。
0
1
2
3
-1
-2
-3
怎么画?
0
1
数轴的画法
2
3
-1
-2
-3
(1)取原点0
(2)规定正方向,通常取向右为正方向
(3)选取适当的长度为单位长度
数轴:规定了原点、正方向、单位长度的
一条直线叫做数轴
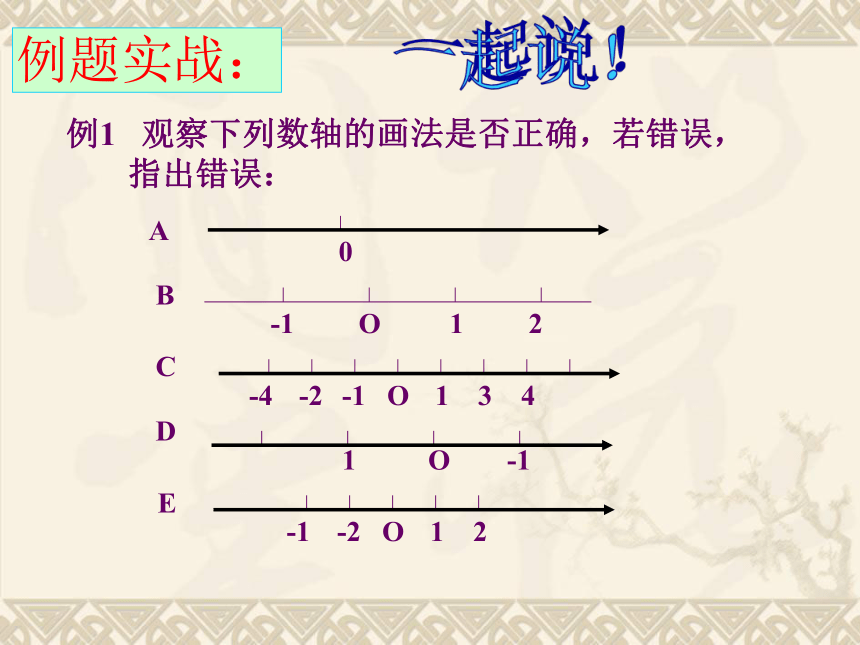
例1
观察下列数轴的画法是否正确,若错误,
指出错误:
0
A
O
1
-1
2
B
-1
O
1
-2
-4
3
4
C
O
1
-1
D
O
1
-1
-2
2
E
例题实战:
一起说!
判断下面所画数轴是否正确,并说明理由。
1.
0
1
-1
2.
4.
6.
8.
3.
7.
5.
9.
10.
-1
0
1
2
-1
-2
1
0
2
-1
1
0
2
-1
0
0
1
-1
0
0
1
-1
2
1
-1
0
1
1
-1
2
-2
1、
小试牛刀:
一起说!
2、是数轴的打“√”,不是数轴的打“×”。 ?
(
×
)
(
×
)
(
√)
+1
-1
小试牛刀:
抢答!
例2.说出下图中数轴上的A、B、C、D、E各点表示什么数?
解:点A表示
–3;
点B表示+1;
点C表示+4;
点D表示-0.5;
点E表示-2.5。
E
D
例题实战:
一起说!
指出数轴上A、B、C、D、
0
1
2
-1
-2
A
B
C
D
E
F
点A表示+2;
点B表示-1;
点C表示0;
点D表示+1.5;
点E表示+1;
点F表示-1.5;
3.
小试牛刀:
一起说!
4.
指出数轴上A、B、C、D各点分别表示什么数?
解:
点B表示
2;
点C表示
0;
点D表示-1。
点A表示-2;
小试牛刀:
抢答!
注意:(1)??
任何一个有理数都可以用数轴上的一个点来表示。
(2)???数轴上的一个点不一定表示一个有理数。
例3.画出数轴,并在数轴上表示下列各数:
-5,
0,-1,+2,??
?,
??
?
-1
-4
-3
-2
0
1
2
3
4
-6
-5
B
A
E
D
C
F
例题实战:
一起说!
5、将某水库一月份五天的水位情况(如下表),
日
期
标
水位
5
10
15
20
25
A
B
C
D
E
0.2
0.1
0
-0.2
-0.1
0
0.1
0.2
-0.1
-0.2
(m)
A
B
C
D
E
小试牛刀:
一起说!
6、在所给数轴上画出表示下列各数的点:
(1)
+3
-2
-1
+2
0
;
(2)
+20
-25
-15
+30
+5
;
0
1
2
-1
-2
0
10
3
-3
-30
30
20
-10
-25
-15
5
20
30
0
2
-2
3
-1
-20
小试牛刀:
抢答!
寻找规律
归纳结论
1.任何一个有理数都能用数轴上点表示吗?
2.哪些数在原点的左边,哪些数在原点的右边,它们到原点的距离分别是多少,由此你发现了什么规律?
结论:一般地,设a是一个正数,则数轴上表示数a的点在原点的(
)边,与原点的距离是(
)个长度单位;表示数-a的点在原点的(
)边,与原点的距离是(
)个长度单位。
左
右
a
a
结论:任何一个有理数都能用数轴上点。但是数轴上的一个点不一定表示一个有理数。
1.
数轴的三要素(
)
A、数轴
原点
正方向
B、正方向
原点
箭头
C、正方形
原点
单位长度
D、负方向
原点
单位长度
C
学以致用
一起说!
下列说法不正确(
)
A.
数轴是一条直线
B.
数轴上所有的点并不都表示有理数
C.
在数轴上表示2和-2的点到原点的距离相等
D.
数轴上一定取向右为正方向
D
学以致用
一起说!
2.若点A在数轴上原点的左边,则A点表示的数是(
)
A.
正数
B.
负数
C.
整数
B
学以致用
一起说!
3.数轴上到原点距离5个单位长度的点表示的数是(
)
A
+5
B
-5
C
C
学以致用
分类讨论思想
抢答!
4.在数轴上原点及原点左边的点所表示的数是(
)
A.
正数
B.
负数
C.
非负数
D.
非正数
D
学以致用
一起说!
5.
在数轴上0与3之间(不包括0,3)还有
个数。(
)
A.
2个
B.
3个
C.
4个
D.
无数个
D
学以致用
抢答!
6.
一个点从数轴的原点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是(
)
A.+6
B.-3
C.+3
D.-9
C
学以致用
抢答!
7.
在数轴上表示数6的点在原点_______侧,到原点的距离是_______个单位长度,表示数-8的点在原点的______侧,到原点的距离是________个单位长度.表示数6的点到表示数-8的点的距离是_______个单位长度.
右
6
左
8
14
学以致用
抢答!
小结
这堂课你什么收获?
你还有什么疑问?
小结:
本节课我们学习了数轴的概念、数轴的画法、有理数在数轴上表示法。
数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
作业
P9练习1、2、3
P14习题1.2第3、4题(在书上写)
家庭作业
基础训练P8
1.2.2
数
轴
义务教育课程标准实验教科书
数学
七年级
上册
1、整数和分数统称有理数
有理数
整数
分数
正整数
零
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
复习旧知:
把下列各数填在相应的集合中:
正数集合:{
};
负数集合:{
};
分数集合:{
};
整数集合:{
};
非负数集合:{
};
有理数集合:{
};
复习旧知:
℃
℃
℃
5
0
-10
请读出下面温度计所表示的温度
新课引入
情境(1)
这样看来,页面所在的刻度就表示此时的温度。说明温度计上的刻度与一些有理数建立了对应关系,也就是说温度计上的每一个刻度都表示一个有理数。
1、怎样用数简明地表示这些树、电线杆与汽车站的相对位置关系?
情境2:
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆。你能用图示的方法表示这一情境吗?
方向和距离
2、生活中还有这种例子吗?请举手列举出来。
3、我们能否利用一个类似于温度计的图形,用它的刻度来表示所有的有理数呢?这就是我们今天一起研究的—数轴。
情境2:
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆。你能用图示的方法表示这一情境吗?
1、观察温度计的刻度规律,你能发现什么?
刻度有正、有负,也有0。
2、类比温度计,你能画图完成上面我们的问题吗?
(1)马路可以用什么几何图形代表?
(2)你认为站牌起什么作用?
(3)你是怎样确定问题中各物体的位置的?
直线
基准点
方向,与站牌的距离
O
0
1
3
7.5
-3
-4.8
探究
1.0代表什么?
2.数的符号的实际意义是什么?
3.如下图,在一条直线上,A,B的距离等于B,C的距离,点B表示3,点C能表示7.5吗?为什么?
4.上述方法表示了这些树、电线杆与汽车站的相对位置关系。例如,-4.8表示位于汽车站西侧4.8米处的电线杆。你能再举个例子吗?
0
1
3
7.5
-3
-4.8
B
A
O
E
C
D
操作与归纳
一般地,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线就叫做“数轴”。
1、画一条水平(或竖直)直线,在直线上任取一点表示数0,这个点做叫原点。
2、通常规定直线上从原点向右(或上)的方向为正方向,从原点向左(或下)的方向为负方向。
3、选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,···;从原点向左,用类似方法依次表示1,2,3,···,就得到了数轴。
0
1
2
3
-1
-2
-3
怎么画?
0
1
数轴的画法
2
3
-1
-2
-3
(1)取原点0
(2)规定正方向,通常取向右为正方向
(3)选取适当的长度为单位长度
数轴:规定了原点、正方向、单位长度的
一条直线叫做数轴
例1
观察下列数轴的画法是否正确,若错误,
指出错误:
0
A
O
1
-1
2
B
-1
O
1
-2
-4
3
4
C
O
1
-1
D
O
1
-1
-2
2
E
例题实战:
一起说!
判断下面所画数轴是否正确,并说明理由。
1.
0
1
-1
2.
4.
6.
8.
3.
7.
5.
9.
10.
-1
0
1
2
-1
-2
1
0
2
-1
1
0
2
-1
0
0
1
-1
0
0
1
-1
2
1
-1
0
1
1
-1
2
-2
1、
小试牛刀:
一起说!
2、是数轴的打“√”,不是数轴的打“×”。 ?
(
×
)
(
×
)
(
√)
+1
-1
小试牛刀:
抢答!
例2.说出下图中数轴上的A、B、C、D、E各点表示什么数?
解:点A表示
–3;
点B表示+1;
点C表示+4;
点D表示-0.5;
点E表示-2.5。
E
D
例题实战:
一起说!
指出数轴上A、B、C、D、
0
1
2
-1
-2
A
B
C
D
E
F
点A表示+2;
点B表示-1;
点C表示0;
点D表示+1.5;
点E表示+1;
点F表示-1.5;
3.
小试牛刀:
一起说!
4.
指出数轴上A、B、C、D各点分别表示什么数?
解:
点B表示
2;
点C表示
0;
点D表示-1。
点A表示-2;
小试牛刀:
抢答!
注意:(1)??
任何一个有理数都可以用数轴上的一个点来表示。
(2)???数轴上的一个点不一定表示一个有理数。
例3.画出数轴,并在数轴上表示下列各数:
-5,
0,-1,+2,??
?,
??
?
-1
-4
-3
-2
0
1
2
3
4
-6
-5
B
A
E
D
C
F
例题实战:
一起说!
5、将某水库一月份五天的水位情况(如下表),
日
期
标
水位
5
10
15
20
25
A
B
C
D
E
0.2
0.1
0
-0.2
-0.1
0
0.1
0.2
-0.1
-0.2
(m)
A
B
C
D
E
小试牛刀:
一起说!
6、在所给数轴上画出表示下列各数的点:
(1)
+3
-2
-1
+2
0
;
(2)
+20
-25
-15
+30
+5
;
0
1
2
-1
-2
0
10
3
-3
-30
30
20
-10
-25
-15
5
20
30
0
2
-2
3
-1
-20
小试牛刀:
抢答!
寻找规律
归纳结论
1.任何一个有理数都能用数轴上点表示吗?
2.哪些数在原点的左边,哪些数在原点的右边,它们到原点的距离分别是多少,由此你发现了什么规律?
结论:一般地,设a是一个正数,则数轴上表示数a的点在原点的(
)边,与原点的距离是(
)个长度单位;表示数-a的点在原点的(
)边,与原点的距离是(
)个长度单位。
左
右
a
a
结论:任何一个有理数都能用数轴上点。但是数轴上的一个点不一定表示一个有理数。
1.
数轴的三要素(
)
A、数轴
原点
正方向
B、正方向
原点
箭头
C、正方形
原点
单位长度
D、负方向
原点
单位长度
C
学以致用
一起说!
下列说法不正确(
)
A.
数轴是一条直线
B.
数轴上所有的点并不都表示有理数
C.
在数轴上表示2和-2的点到原点的距离相等
D.
数轴上一定取向右为正方向
D
学以致用
一起说!
2.若点A在数轴上原点的左边,则A点表示的数是(
)
A.
正数
B.
负数
C.
整数
B
学以致用
一起说!
3.数轴上到原点距离5个单位长度的点表示的数是(
)
A
+5
B
-5
C
C
学以致用
分类讨论思想
抢答!
4.在数轴上原点及原点左边的点所表示的数是(
)
A.
正数
B.
负数
C.
非负数
D.
非正数
D
学以致用
一起说!
5.
在数轴上0与3之间(不包括0,3)还有
个数。(
)
A.
2个
B.
3个
C.
4个
D.
无数个
D
学以致用
抢答!
6.
一个点从数轴的原点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是(
)
A.+6
B.-3
C.+3
D.-9
C
学以致用
抢答!
7.
在数轴上表示数6的点在原点_______侧,到原点的距离是_______个单位长度,表示数-8的点在原点的______侧,到原点的距离是________个单位长度.表示数6的点到表示数-8的点的距离是_______个单位长度.
右
6
左
8
14
学以致用
抢答!
小结
这堂课你什么收获?
你还有什么疑问?
小结:
本节课我们学习了数轴的概念、数轴的画法、有理数在数轴上表示法。
数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
作业
P9练习1、2、3
P14习题1.2第3、4题(在书上写)
家庭作业
基础训练P8
