人教版数学九年级上册 24.1.4圆周角的概念和圆周角的定理教案(第1课时)
文档属性
| 名称 | 人教版数学九年级上册 24.1.4圆周角的概念和圆周角的定理教案(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 19:51:14 | ||
图片预览

文档简介
§24.1.4圆周角
第1课时《圆周角及圆周角定理》教学设计
教材分析
《圆周角》是九年级数学上册第二十四章《圆》这一章中的重要一节,它是引入圆心角之后又学习的另一个与圆有关的重要的角,圆周角及圆周角定理是这一章的基本概念和定理,学生掌握的熟练程度直接影响着学生后续知识的学习。因此让学生多角度、多层次地理解并掌握圆周角的定义和定理,有着十分重要的作用。
学情分析
在此之前,学生已经掌握了圆心角的定义,对圆心角及所对弧的度数的关系有了认识,因此在学习圆周角的定义时,学生会对圆内的又一类角很有兴致,同时圆周角的定义是类比圆心角得到的,让学生体会类比思想的重要性,而圆周角定理的证明用到了完全归纳法,分为三种情况证明,对于学生有些难度。
教学目标
1、圆周角的概念,探索并证明圆周角定理并能应用圆周角定理,解决简单问题。
2、探索圆周角的过程中,培养动手操作、自主探索与合作交流的能力,体会分情况逐一证明的必要性。
3、在互相交流的过程中,培养解决数学问题的能力,激发学习数学的兴趣。
重点难点分析
重点:探索同弧所对的圆周角与圆心角度数的关系.
难点:探究圆周角与圆心的位置关系,证明圆周角定理.
教学课型
新授课
教学方法
启发引导
小组探究
为了体现学生为主体,教师为主导,知识为主线,育人为主旨的教学原则,本节课主要采用探究式教学法为主线,多媒体直观演示、启发引导为辅的教学方法.
学法指导
知识是通过学生自己动口、动手、动脑,积极思考、主动探索获得.我将课堂交给学生,让学生自己去探索,发现验证知识.自主探索,研讨发现,得出结论是本节课主要的学习方法.
教具准备
教师:多媒体课件、圆规、三角板等
学生:直尺、圆规、量角器等
教学过程设计
创设情境
合作探究
归纳总结
应用练习
课堂小结
课堂检测
教学活动
1、
课前复习
上一堂课我们一起学习了与圆有关的一类特殊角——圆心角及其性质,请同学们思考并回答,什么叫圆心角?
圆心角有那些性质?
二、创设情境,引入新知
情境
出示多媒体课件:
足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练,甲、乙两名运动员分别在C、D两处,他们都说在自己所在位置对球门AB的张角大,(甲对球门AB的张角为∠C,乙对球门AB的张角为∠D)你认为他们谁说的对?
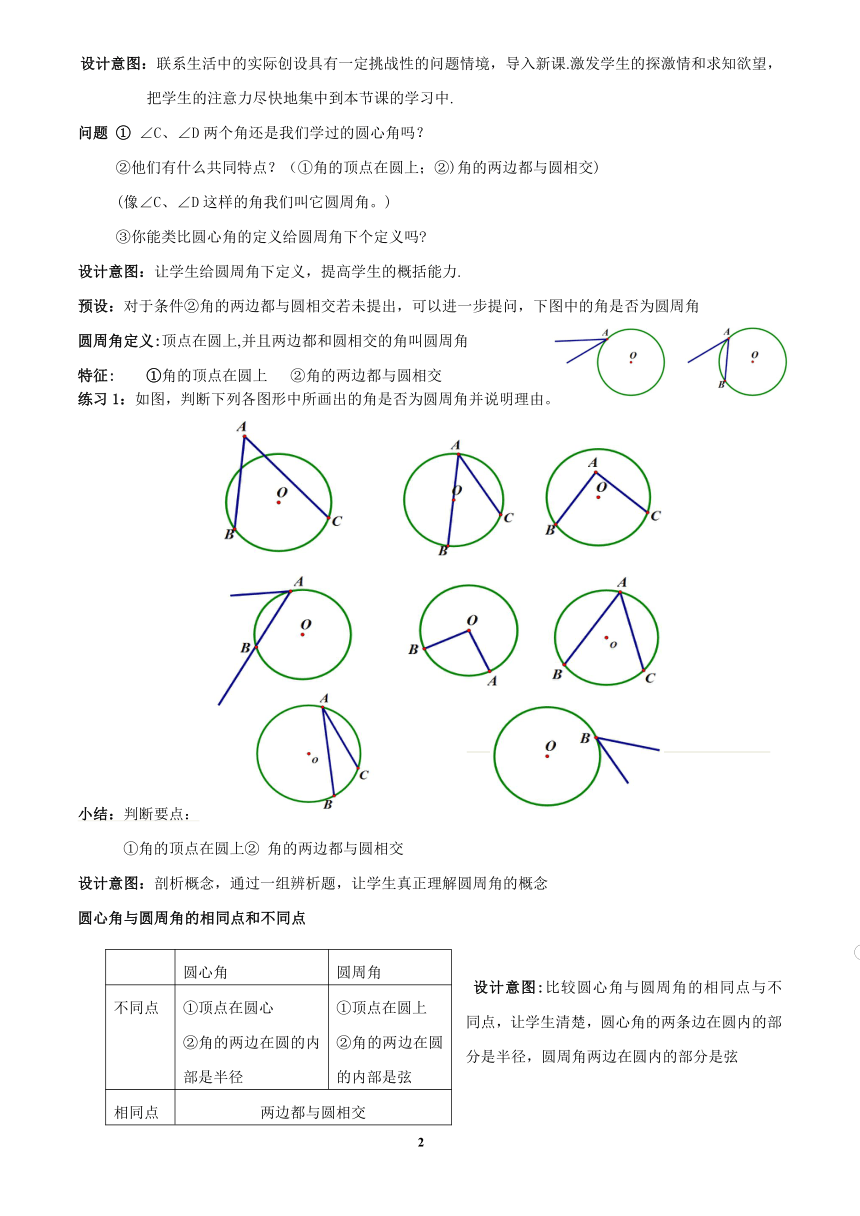
设计意图:联系生活中的实际创设具有一定挑战性的问题情境,导入新课.激发学生的探激情和求知欲望,把学生的注意力尽快地集中到本节课的学习中.
问题
①
∠C、∠D两个角还是我们学过的圆心角吗?
②他们有什么共同特点?(①角的顶点在圆上;②)角的两边都与圆相交)
(像∠C、∠D这样的角我们叫它圆周角。)
③你能类比圆心角的定义给圆周角下个定义吗?
设计意图:让学生给圆周角下定义,提高学生的概括能力.
预设:对于条件②角的两边都与圆相交若未提出,可以进一步提问,下图中的角是否为圆周角
圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角
特征:
①角的顶点在圆上
②角的两边都与圆相交
练习1:如图,判断下列各图形中所画出的角是否为圆周角并说明理由。
小结:判断要点:
①角的顶点在圆上②
角的两边都与圆相交
设计意图:剖析概念,通过一组辨析题,让学生真正理解圆周角的概念
圆心角与圆周角的相同点和不同点
圆心角
圆周角
不同点
①顶点在圆心②角的两边在圆的内部是半径
①顶点在圆上②角的两边在圆的内部是弦
相同点
两边都与圆相交
1
设计意图:比较圆心角与圆周角的相同点与不同点,让学生清楚,圆心角的两条边在圆内的部分是半径,圆周角两边在圆内的部分是弦
3、
合作探究,学习新知
一条弧所对的圆周角与它所对的圆心角之间有怎样的数量关系?
问题
1画圆O,在圆O上任取一段,那么它所对的圆心角有几个?
所对的圆周角有多少个呢?(任取优弧上一点,连接的两个端点即为所对的一个圆周角)
问题2:你能否把这无数个圆周角进行分类?若能,可以分成几类?分类的依据是什么?
分析图形:以圆心和圆周角的位置关系分类的:圆周角与圆心的位置关系有如图的三种情况
①圆心在圆周角一条边上
②圆心在圆周角内
③圆心在圆周角外
问题3:探究所对的圆周角与它所对的圆心角之间有怎样的数量关系?
(1)测量上面图中三种情况下的所对的圆心角∠AOB和一个圆周角∠ACB的度数。
所对的圆周角∠
=______
所对的圆心角∠
=______
所对的圆周角∠
=______
所对的圆心角∠
=______
所对的圆周角∠
=______
所对的圆心角∠
=______
设计意图:学生亲手度量,进行实验、探究、得出结论。激发学生求知欲望。
(2)观察测量结果你有什么发现?
(∠ACB=∠AOB.)
(3)你得出了什么猜想?
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
(4)怎样验证你的猜想?
(利用几何推理进行证明)
设计意图:引导学生探究、初步感知发现圆周角定理。
分析图形:圆周角与圆心的位置关系有如图的三种情况:
①心在圆周角一条边上
②圆心在圆周角内
③圆心在圆周角外
由于有图形分为三类,所以我们必须分为三种情况来证明定理。
在证明之前,先要将我们所要证明的命题转化为数学语言,分析出命题的已知和求证
设计意图:这一过程体现了数学
(?http:?/??/?www.teachercn.com?/?ShuXue?/?"
\t
"_blank?)中的分类讨论的思想
已知:⊙O中所对的圆周角为∠ACB,
所对的圆心角为∠AOB求证:∠ACB=∠AOB.
验证猜想,定理的证明思路:
我们根据圆周角与圆心的位置关系,分三种情况来说明.先解决特殊问题,首先解决第一种圆心在圆周角边上的特殊情况的证明过程,再把其他两种情况转化为特殊问题来解决.
(1)证明圆心在圆周角边上的情况:
证明:∵OC=OB,
∴∠C=∠B.
又
∵∠AOB=∠C+∠B,
∴∠C=∠AOB.
分析证明过程中所用的到条件:①直径(过圆周角顶点的直径)②等腰三角形③三角形外角定理
图形的特点:可看成是由三条线段围成的,一是过圆周角顶点的直径;二是圆周角在圆内的部分—弦
三是:圆心角在圆内的部分——半径
引导学生用以上三点知识证明下面的两种情况。给学生时间讨论以下两种情况的证明,教师巡视,提醒学生构造条件
设计意图:在证明中,后两种都化成了第一种情况,这体现数学
(?http:?/??/?www.teachercn.com?/?ShuXue?/?"
\t
"_blank?)中从特殊到一般的化归思想.从而让学生学会了一种分析问题解决问题的方式方法。
(2)证明圆心在圆周角内部的情况:
学生一时难以找到证明的途径,引导学生将图形②通过添加过圆周角顶点C的直径转化为图形①解决.
证明:
过圆周角的顶点C作圆O的直径CD,利用(1)的结论得:
∠1=∠2.
∠3=∠4.
∴∠1+∠3=∠2+∠4=
(∠2+∠4)
即:∠ACB=∠AOB.
(3)证明圆心在圆周角外部的情况:
证明:过圆周角顶点C作圆O的直径CD.
利用(1)的结论得:
∠1=∠2.∠BCD=∠BOD.
∴∠BCD-∠1=∠BOD-∠2=
(∠BOD
-∠2)
即:∠ABC=∠AOB.
小结:指出这种将一般的、复杂的问题转换为特殊的、简单的问题的思想就是转化思想,是解决数学问题的一种行之有效的方法。
四、
归纳总结,得出结论
设计意图:文字语言与数学语言之间的转化能力
结论:
定理:一条弧所对的圆周角等于它所对的圆心角的一半
符号:所对的圆周角为∠ACB,
所对的圆心角为∠AOB
∠ACB=∠AOB.
定理剖析:①同一条
②周角等于圆心角的一半
五、应用练习
设计意图:利用本节课所学的内容解决问题,同时巩固本节课所学的内容。
练习2.填空
(1)已知:如图,若圆心角∠BOC的度数为100°,则圆周角∠BAC的度数为____________.
(2)已知:如图,点A、P、B是⊙O上的三点,若∠APB=25°,则∠AOB的度数为___________.
(3)已知:如图,△ABC内接于⊙O,∠OBC=25°,则∠A的度数为__________.
练习3:回到课前的问题。
足球训练场上教练在球门前划了一个圆圈射门训练,甲、乙两名运动员分别在C、D两处,他们都说在自己所在位置对球门AB的张角大,你认为他们谁说的对?
解:连接OA、OB,由圆周角定理可知:
小结:一般情况下,圆周角的问题可以转化为它同弧所对的圆心角的问题来解决。
六、课堂小结
说一说
这堂课你有什么收获
学生反思、体会课堂中所学内容并归纳总结,教师补充
知识:
①圆周角的定义②圆周角定理
数学思想:①类比思想②分类思想③转化思想
设计意图:通过小结使学生归纳、梳理总结本节的知识
七、课堂作业
1.已知:如图,若圆周角∠BAC的度数为30°,则圆心角∠BOC的度数为____________.
2.已知:如图,点A、P、B是⊙O上的三点,若∠AOB=50°,则∠APB的度数为___________.
3.已知:如图,△ABC内接于⊙O,∠A=60°,则∠OBC的度数为__________.
板书设计
§22.4圆周角及圆周角定理
1、圆周角定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
特
征:
①
角的顶点在圆上.②
角的两边都与圆相交.
2、圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半。
符号语言:
三种情况分类
①
②
③
1
5
第1课时《圆周角及圆周角定理》教学设计
教材分析
《圆周角》是九年级数学上册第二十四章《圆》这一章中的重要一节,它是引入圆心角之后又学习的另一个与圆有关的重要的角,圆周角及圆周角定理是这一章的基本概念和定理,学生掌握的熟练程度直接影响着学生后续知识的学习。因此让学生多角度、多层次地理解并掌握圆周角的定义和定理,有着十分重要的作用。
学情分析
在此之前,学生已经掌握了圆心角的定义,对圆心角及所对弧的度数的关系有了认识,因此在学习圆周角的定义时,学生会对圆内的又一类角很有兴致,同时圆周角的定义是类比圆心角得到的,让学生体会类比思想的重要性,而圆周角定理的证明用到了完全归纳法,分为三种情况证明,对于学生有些难度。
教学目标
1、圆周角的概念,探索并证明圆周角定理并能应用圆周角定理,解决简单问题。
2、探索圆周角的过程中,培养动手操作、自主探索与合作交流的能力,体会分情况逐一证明的必要性。
3、在互相交流的过程中,培养解决数学问题的能力,激发学习数学的兴趣。
重点难点分析
重点:探索同弧所对的圆周角与圆心角度数的关系.
难点:探究圆周角与圆心的位置关系,证明圆周角定理.
教学课型
新授课
教学方法
启发引导
小组探究
为了体现学生为主体,教师为主导,知识为主线,育人为主旨的教学原则,本节课主要采用探究式教学法为主线,多媒体直观演示、启发引导为辅的教学方法.
学法指导
知识是通过学生自己动口、动手、动脑,积极思考、主动探索获得.我将课堂交给学生,让学生自己去探索,发现验证知识.自主探索,研讨发现,得出结论是本节课主要的学习方法.
教具准备
教师:多媒体课件、圆规、三角板等
学生:直尺、圆规、量角器等
教学过程设计
创设情境
合作探究
归纳总结
应用练习
课堂小结
课堂检测
教学活动
1、
课前复习
上一堂课我们一起学习了与圆有关的一类特殊角——圆心角及其性质,请同学们思考并回答,什么叫圆心角?
圆心角有那些性质?
二、创设情境,引入新知
情境
出示多媒体课件:
足球训练场上教练在球门前划了一个圆圈进行无人防守的射门训练,甲、乙两名运动员分别在C、D两处,他们都说在自己所在位置对球门AB的张角大,(甲对球门AB的张角为∠C,乙对球门AB的张角为∠D)你认为他们谁说的对?
设计意图:联系生活中的实际创设具有一定挑战性的问题情境,导入新课.激发学生的探激情和求知欲望,把学生的注意力尽快地集中到本节课的学习中.
问题
①
∠C、∠D两个角还是我们学过的圆心角吗?
②他们有什么共同特点?(①角的顶点在圆上;②)角的两边都与圆相交)
(像∠C、∠D这样的角我们叫它圆周角。)
③你能类比圆心角的定义给圆周角下个定义吗?
设计意图:让学生给圆周角下定义,提高学生的概括能力.
预设:对于条件②角的两边都与圆相交若未提出,可以进一步提问,下图中的角是否为圆周角
圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角
特征:
①角的顶点在圆上
②角的两边都与圆相交
练习1:如图,判断下列各图形中所画出的角是否为圆周角并说明理由。
小结:判断要点:
①角的顶点在圆上②
角的两边都与圆相交
设计意图:剖析概念,通过一组辨析题,让学生真正理解圆周角的概念
圆心角与圆周角的相同点和不同点
圆心角
圆周角
不同点
①顶点在圆心②角的两边在圆的内部是半径
①顶点在圆上②角的两边在圆的内部是弦
相同点
两边都与圆相交
1
设计意图:比较圆心角与圆周角的相同点与不同点,让学生清楚,圆心角的两条边在圆内的部分是半径,圆周角两边在圆内的部分是弦
3、
合作探究,学习新知
一条弧所对的圆周角与它所对的圆心角之间有怎样的数量关系?
问题
1画圆O,在圆O上任取一段,那么它所对的圆心角有几个?
所对的圆周角有多少个呢?(任取优弧上一点,连接的两个端点即为所对的一个圆周角)
问题2:你能否把这无数个圆周角进行分类?若能,可以分成几类?分类的依据是什么?
分析图形:以圆心和圆周角的位置关系分类的:圆周角与圆心的位置关系有如图的三种情况
①圆心在圆周角一条边上
②圆心在圆周角内
③圆心在圆周角外
问题3:探究所对的圆周角与它所对的圆心角之间有怎样的数量关系?
(1)测量上面图中三种情况下的所对的圆心角∠AOB和一个圆周角∠ACB的度数。
所对的圆周角∠
=______
所对的圆心角∠
=______
所对的圆周角∠
=______
所对的圆心角∠
=______
所对的圆周角∠
=______
所对的圆心角∠
=______
设计意图:学生亲手度量,进行实验、探究、得出结论。激发学生求知欲望。
(2)观察测量结果你有什么发现?
(∠ACB=∠AOB.)
(3)你得出了什么猜想?
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
(4)怎样验证你的猜想?
(利用几何推理进行证明)
设计意图:引导学生探究、初步感知发现圆周角定理。
分析图形:圆周角与圆心的位置关系有如图的三种情况:
①心在圆周角一条边上
②圆心在圆周角内
③圆心在圆周角外
由于有图形分为三类,所以我们必须分为三种情况来证明定理。
在证明之前,先要将我们所要证明的命题转化为数学语言,分析出命题的已知和求证
设计意图:这一过程体现了数学
(?http:?/??/?www.teachercn.com?/?ShuXue?/?"
\t
"_blank?)中的分类讨论的思想
已知:⊙O中所对的圆周角为∠ACB,
所对的圆心角为∠AOB求证:∠ACB=∠AOB.
验证猜想,定理的证明思路:
我们根据圆周角与圆心的位置关系,分三种情况来说明.先解决特殊问题,首先解决第一种圆心在圆周角边上的特殊情况的证明过程,再把其他两种情况转化为特殊问题来解决.
(1)证明圆心在圆周角边上的情况:
证明:∵OC=OB,
∴∠C=∠B.
又
∵∠AOB=∠C+∠B,
∴∠C=∠AOB.
分析证明过程中所用的到条件:①直径(过圆周角顶点的直径)②等腰三角形③三角形外角定理
图形的特点:可看成是由三条线段围成的,一是过圆周角顶点的直径;二是圆周角在圆内的部分—弦
三是:圆心角在圆内的部分——半径
引导学生用以上三点知识证明下面的两种情况。给学生时间讨论以下两种情况的证明,教师巡视,提醒学生构造条件
设计意图:在证明中,后两种都化成了第一种情况,这体现数学
(?http:?/??/?www.teachercn.com?/?ShuXue?/?"
\t
"_blank?)中从特殊到一般的化归思想.从而让学生学会了一种分析问题解决问题的方式方法。
(2)证明圆心在圆周角内部的情况:
学生一时难以找到证明的途径,引导学生将图形②通过添加过圆周角顶点C的直径转化为图形①解决.
证明:
过圆周角的顶点C作圆O的直径CD,利用(1)的结论得:
∠1=∠2.
∠3=∠4.
∴∠1+∠3=∠2+∠4=
(∠2+∠4)
即:∠ACB=∠AOB.
(3)证明圆心在圆周角外部的情况:
证明:过圆周角顶点C作圆O的直径CD.
利用(1)的结论得:
∠1=∠2.∠BCD=∠BOD.
∴∠BCD-∠1=∠BOD-∠2=
(∠BOD
-∠2)
即:∠ABC=∠AOB.
小结:指出这种将一般的、复杂的问题转换为特殊的、简单的问题的思想就是转化思想,是解决数学问题的一种行之有效的方法。
四、
归纳总结,得出结论
设计意图:文字语言与数学语言之间的转化能力
结论:
定理:一条弧所对的圆周角等于它所对的圆心角的一半
符号:所对的圆周角为∠ACB,
所对的圆心角为∠AOB
∠ACB=∠AOB.
定理剖析:①同一条
②周角等于圆心角的一半
五、应用练习
设计意图:利用本节课所学的内容解决问题,同时巩固本节课所学的内容。
练习2.填空
(1)已知:如图,若圆心角∠BOC的度数为100°,则圆周角∠BAC的度数为____________.
(2)已知:如图,点A、P、B是⊙O上的三点,若∠APB=25°,则∠AOB的度数为___________.
(3)已知:如图,△ABC内接于⊙O,∠OBC=25°,则∠A的度数为__________.
练习3:回到课前的问题。
足球训练场上教练在球门前划了一个圆圈射门训练,甲、乙两名运动员分别在C、D两处,他们都说在自己所在位置对球门AB的张角大,你认为他们谁说的对?
解:连接OA、OB,由圆周角定理可知:
小结:一般情况下,圆周角的问题可以转化为它同弧所对的圆心角的问题来解决。
六、课堂小结
说一说
这堂课你有什么收获
学生反思、体会课堂中所学内容并归纳总结,教师补充
知识:
①圆周角的定义②圆周角定理
数学思想:①类比思想②分类思想③转化思想
设计意图:通过小结使学生归纳、梳理总结本节的知识
七、课堂作业
1.已知:如图,若圆周角∠BAC的度数为30°,则圆心角∠BOC的度数为____________.
2.已知:如图,点A、P、B是⊙O上的三点,若∠AOB=50°,则∠APB的度数为___________.
3.已知:如图,△ABC内接于⊙O,∠A=60°,则∠OBC的度数为__________.
板书设计
§22.4圆周角及圆周角定理
1、圆周角定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
特
征:
①
角的顶点在圆上.②
角的两边都与圆相交.
2、圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半。
符号语言:
三种情况分类
①
②
③
1
5
同课章节目录
