人教版数学九年级上册24.1.4圆周角的概念和圆周角的定理课件(17张)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角的概念和圆周角的定理课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 449.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 07:14:11 | ||
图片预览


文档简介
(共17张PPT)
2013人教版九年级数学(上)
24.1.4圆周角
学习目标
1理解圆周角概念,识别圆周角。
2掌握圆周角定理。
3体会几何定理学习的特点。
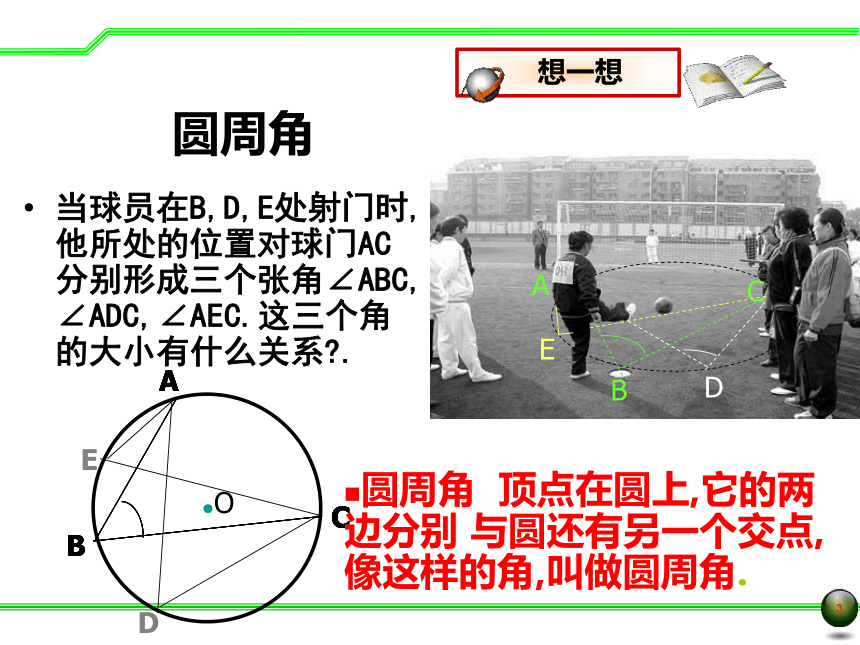
圆周角
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,
∠ADC,∠AEC.这三个角的大小有什么关系?.
想一想
●O
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
D
E
D
E
圆周角
顶点在圆上,它的两边分别
与圆还有另一个交点,像这样的角,叫做圆周角.
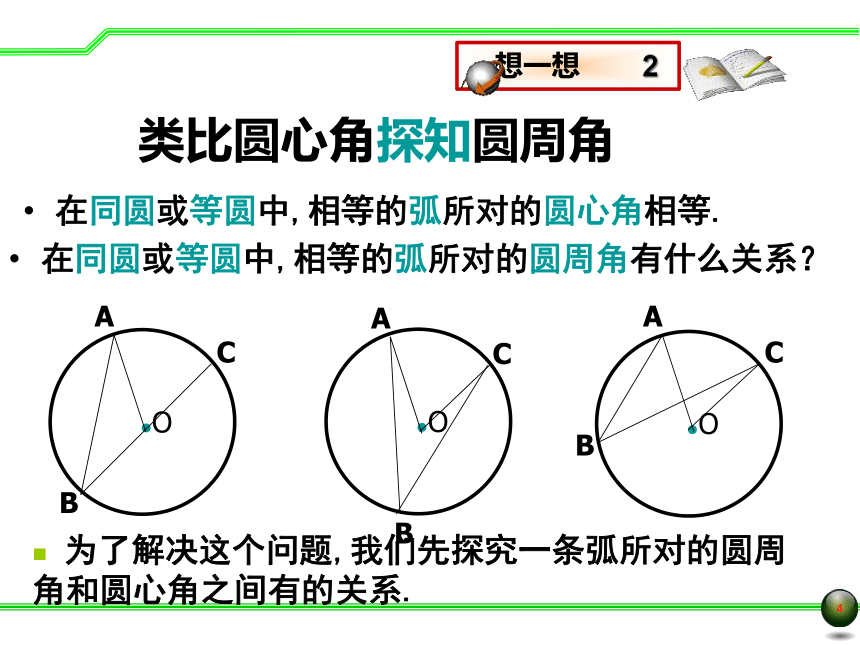
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
想一想
2
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
●O
●O
●O
A
B
C
A
B
C
A
B
C
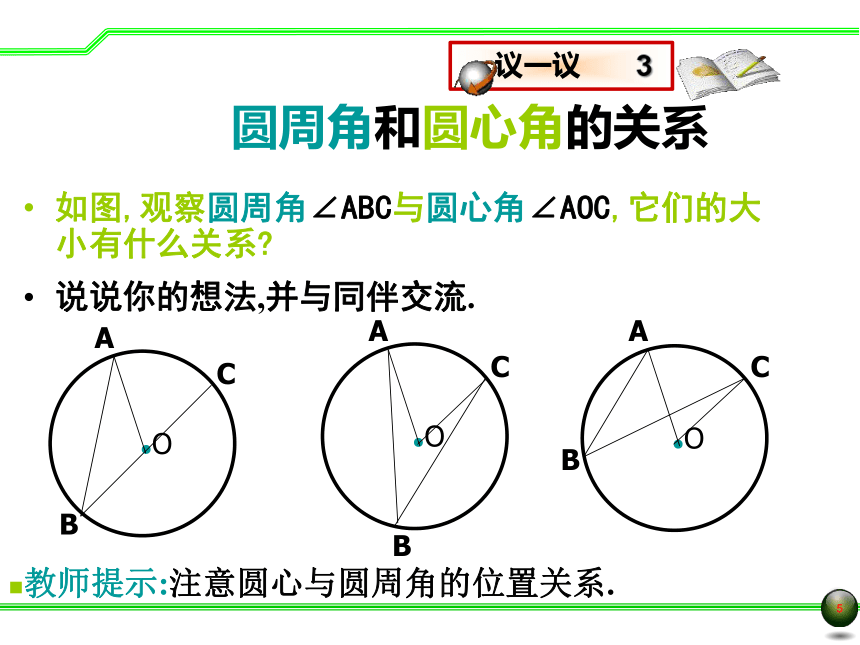
圆周角和圆心角的关系
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
议一议
3
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角和圆心角的关系
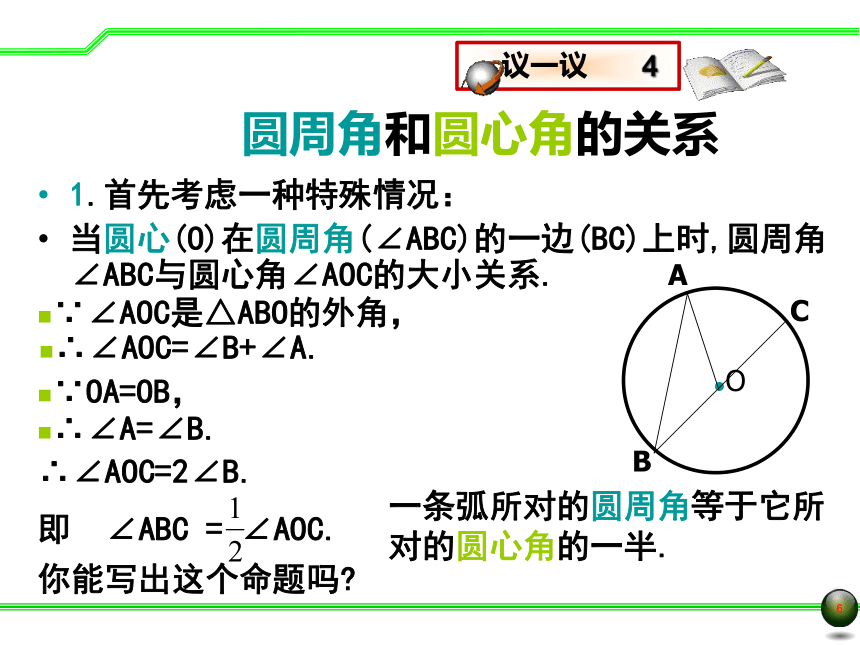
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
议一议
4
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
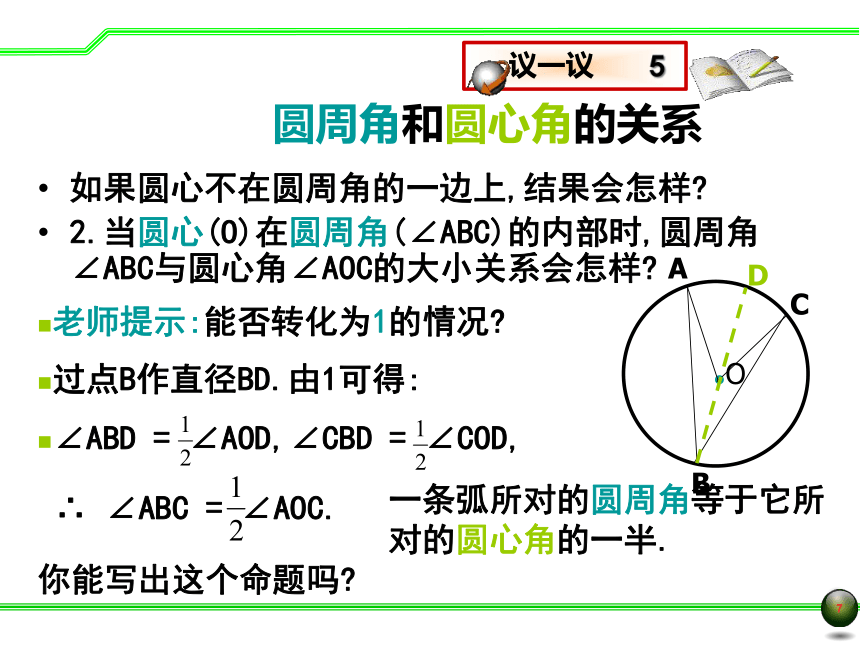
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
议一议
5
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD
=
∠AOD,∠CBD
=
∠COD,
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
议一议
6
老师提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD
=
∠AOD,∠CBD
=
∠COD,
A
B
C
圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
议一议
7
●O
A
B
C
●O
A
B
C
●O
A
B
C
即
∠ABC
=
∠AOC.
思考与巩固
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
随堂练习
8
●O
B
A
C
解:
∠A
=
∠BOC
=
25°.
2.如图(2),在⊙O中,∠BAD=50°,
求∠C的大小.
A
●O
C
B
D
四边形与圆的位置关系
如果四边形的四个顶点在一个圆,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.
●O
A
B
C
D
D
如图:圆内接四边形ABCD中,
∵
∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°,
∴∠BAD+∠BCD=
180°.
同理∠ABC+∠ADC=180°.
圆内接四边形的对角互补.
C
O
B
A
如果延长BC到E,那么
∠DCE+∠BCD
=
180°.
∴∠A=∠DCE.
又
∵∠A
+∠BCD=
180°,
C
O
D
B
A
E
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.
圆内接四边形的一个外角等于它的内对角.
四边形与圆的位置关系
1.圆内接四边形对角互补.
2.圆内接四边形所对的一个外角等于它的内对角.
3.对角互补的四边形内接于圆.
●O
A
B
C
D
猜一猜
9
1.如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
2.想一想,等圆中也有这样的结论吗?
●O
B
A
C
D
E
同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
挑战自我
p88
练习1.2.3题
祝你成功!
独立作业
10
驶向胜利的彼岸
结束寄语
要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.
下课了!
再见
2013人教版九年级数学(上)
24.1.4圆周角
学习目标
1理解圆周角概念,识别圆周角。
2掌握圆周角定理。
3体会几何定理学习的特点。
圆周角
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,
∠ADC,∠AEC.这三个角的大小有什么关系?.
想一想
●O
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
D
E
D
E
圆周角
顶点在圆上,它的两边分别
与圆还有另一个交点,像这样的角,叫做圆周角.
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
想一想
2
为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间有的关系.
●O
●O
●O
A
B
C
A
B
C
A
B
C
圆周角和圆心角的关系
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?
说说你的想法,并与同伴交流.
议一议
3
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
议一议
4
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样?
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
议一议
5
老师提示:能否转化为1的情况?
过点B作直径BD.由1可得:
●O
∴
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD
=
∠AOD,∠CBD
=
∠COD,
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样?
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
议一议
6
老师提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
●O
∴
∠ABC
=
∠AOC.
你能写出这个命题吗?
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD
=
∠AOD,∠CBD
=
∠COD,
A
B
C
圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
议一议
7
●O
A
B
C
●O
A
B
C
●O
A
B
C
即
∠ABC
=
∠AOC.
思考与巩固
1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
随堂练习
8
●O
B
A
C
解:
∠A
=
∠BOC
=
25°.
2.如图(2),在⊙O中,∠BAD=50°,
求∠C的大小.
A
●O
C
B
D
四边形与圆的位置关系
如果四边形的四个顶点在一个圆,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.
●O
A
B
C
D
D
如图:圆内接四边形ABCD中,
∵
∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°,
∴∠BAD+∠BCD=
180°.
同理∠ABC+∠ADC=180°.
圆内接四边形的对角互补.
C
O
B
A
如果延长BC到E,那么
∠DCE+∠BCD
=
180°.
∴∠A=∠DCE.
又
∵∠A
+∠BCD=
180°,
C
O
D
B
A
E
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.
圆内接四边形的一个外角等于它的内对角.
四边形与圆的位置关系
1.圆内接四边形对角互补.
2.圆内接四边形所对的一个外角等于它的内对角.
3.对角互补的四边形内接于圆.
●O
A
B
C
D
猜一猜
9
1.如图,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?
2.想一想,等圆中也有这样的结论吗?
●O
B
A
C
D
E
同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
挑战自我
p88
练习1.2.3题
祝你成功!
独立作业
10
驶向胜利的彼岸
结束寄语
要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.
下课了!
再见
同课章节目录
