人教版数学九年级上册:24.1.3弧、弦、圆心角 课件(25张ppt)
文档属性
| 名称 | 人教版数学九年级上册:24.1.3弧、弦、圆心角 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
义务教育课程标准实验教科书
九年级
上册
人民教育出版社
24.1.3
弧、弦、圆心角
圆是中心对称图形吗?它的对称中心在哪里?
·
一、思考
圆是中心对称图形,
它的对称中心是圆心.
·
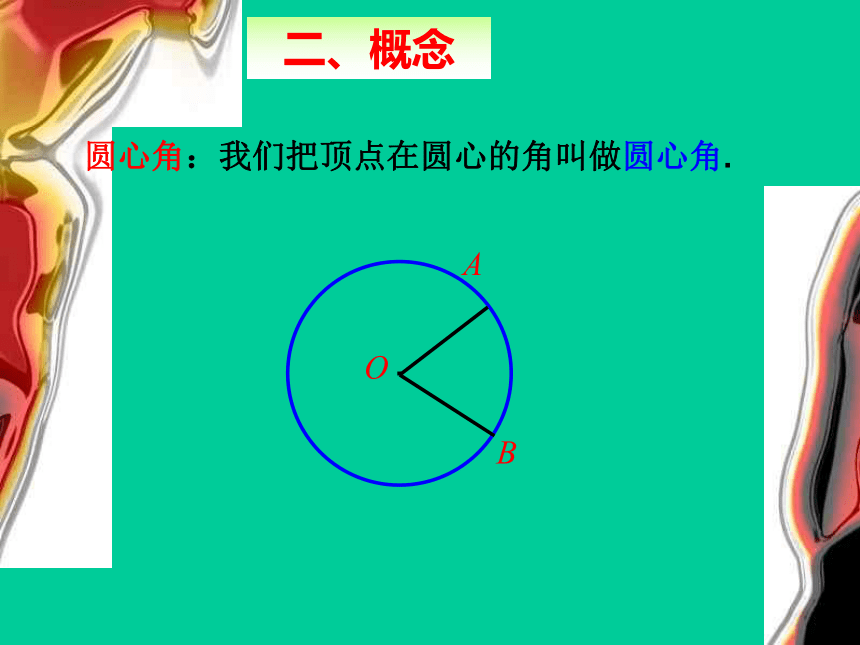
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
二、概念
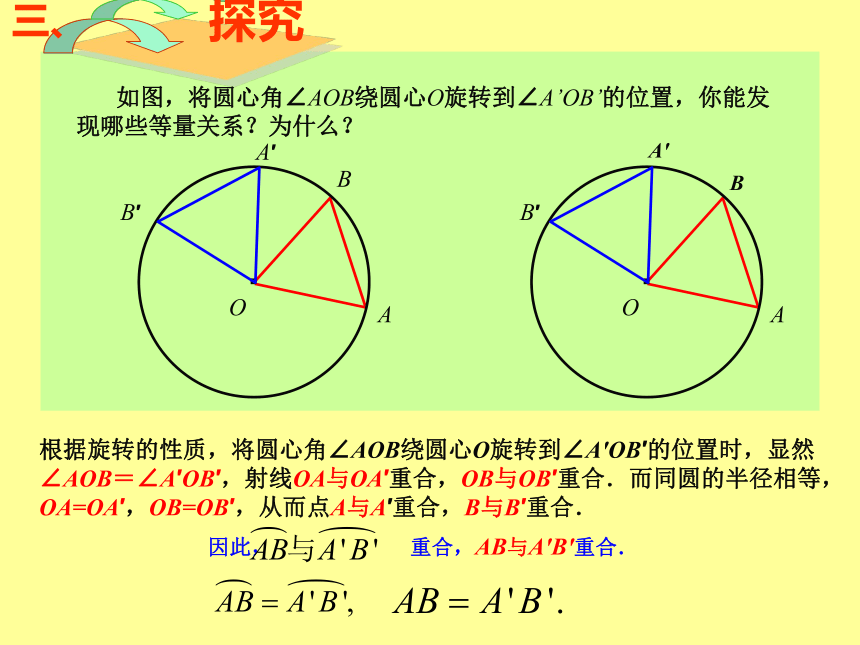
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.
·
O
A
B
探究
·
O
A
B
A′
B′
A′
B′
三、
因此,
重合,AB与A′B′重合.
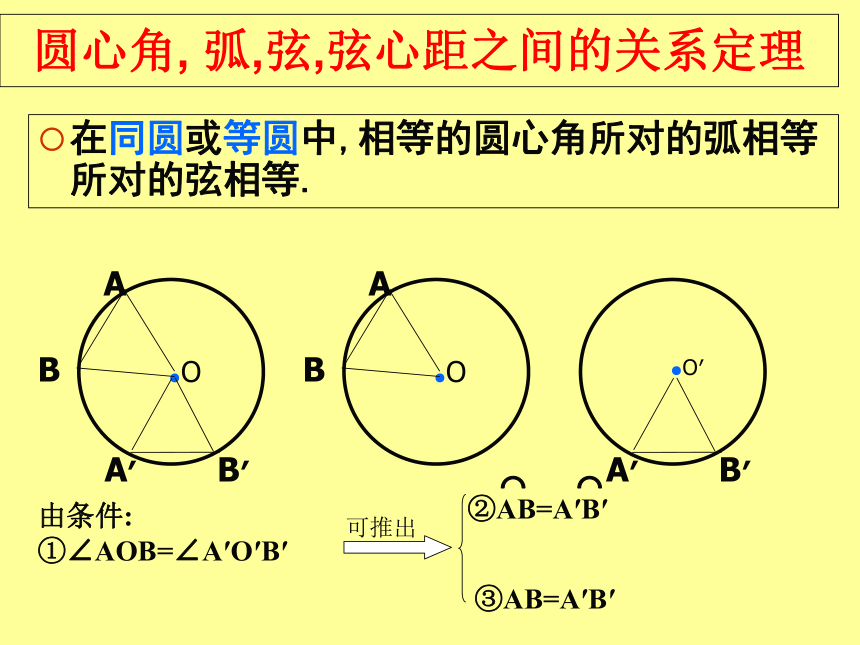
圆心角,
弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.
●O
A
B
A′
B′
●O
A
B
●O′
A′
B′
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
可推出
A′
B′
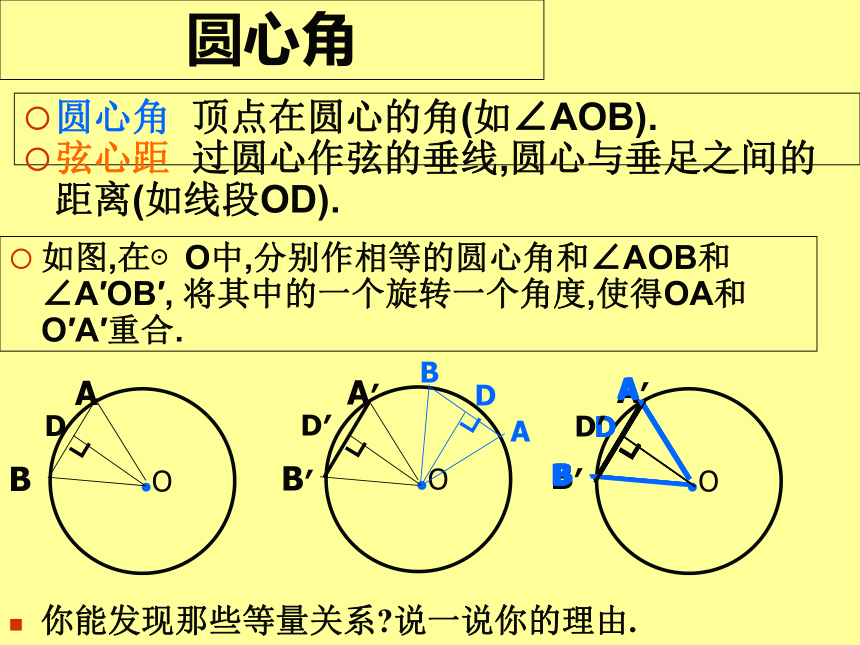
圆心角
圆心角
顶点在圆心的角(如∠AOB).
弦心距
过圆心作弦的垂线,圆心与垂足之间的距离(如线段OD).
如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′,
将其中的一个旋转一个角度,使得OA和O′A′重合.
你能发现那些等量关系?说一说你的理由.
●O
●O
A
B
┓
D
●O
A
B
┓
D
A
B
A
B
A
B
A
B
A
B
A
B
┓
D
┓
D
┓
D
┓
D
┓
D
┓
D′
A′
B′
┓
D′
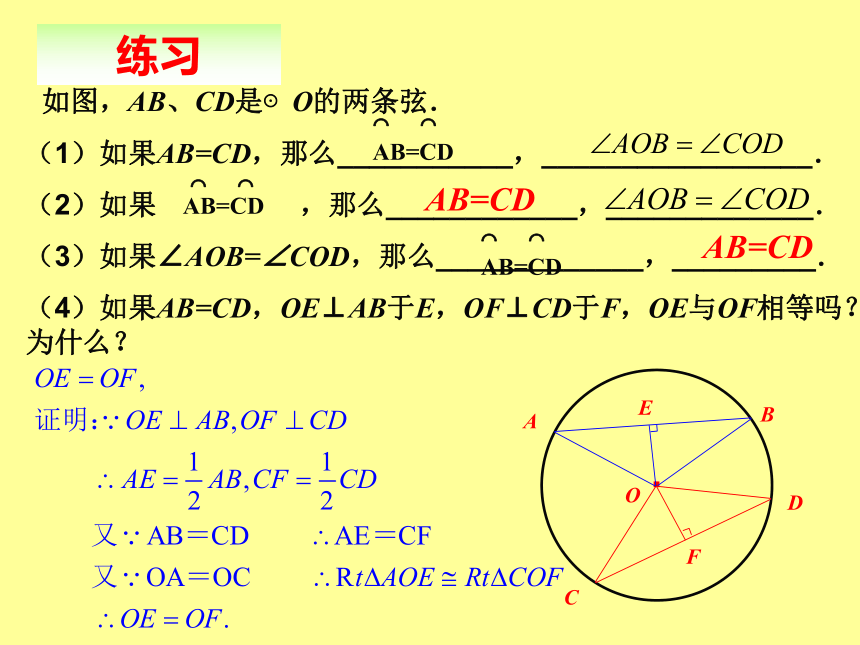
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
练习
AB=CD
⌒
⌒
⌒
⌒
AB=CD
⌒
⌒
AB=CD
圆心角,
弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
在同圆或等圆中,如果轮换下面五组条件:
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____,
所对的弦________,所对的弦的弦心距________
。
;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________,所对的弦的弦心距________
.
这样,我们就得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦相等,所对的弦的弦心距也相等。
相等
相等
相等
相等
同圆或等圆中,
两个圆心角、
两条弧、两条
弦中有一组量
相等,它们所
对应的其余各
组量也相等.
四、定理
相等
相等
推论
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
①∠AOB=∠A′O′B′
?O
A
B
C
D
E
F
已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?
想一想?
1°圆心角
1°弧
C
D
n°圆心角
n°弧
把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角。1°的圆心角所对的弧叫做1°的弧。
圆心角的度数和它所对的弧的度数相等。
一般地,n°的圆心角对着n°的弧。
弧的度数
如图,AB、CD是⊙O的两条弦,
OE、OF为AB、CD的弦心距,
如果AB=CD,那么
,
,
;
如果OE=OF,那么
,
,
;
如果弧AB=弧CD,那么
,
,
;
如果∵∠AOB=∠COD,那么
,
,
。
下列说法正确吗?为什么?
在⊙O和⊙O’中,∵∠AOB=∠A’O’B’∴AB=A’B’
在⊙O和⊙O’中,∵AB=A’B’,∴弧AB=弧A’B’
注意前提:
在同圆或等圆中
O
A
B
E
C
D
F
复习回顾
证明:∵
∴
AB=AC,
△ABC等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形,AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
·
A
B
C
O
五、例题
例如图在⊙O中,
,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
1如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
解:
练习
2已知:如图,点P在⊙O上,点O在∠EPF的平分线上,∠
EPF的两边交⊙O于点A和B。
求证:PA=PB.
E
F
A
B
P
O
基础练习
3已知:如图,点O在∠EPF的平分线上,⊙O和∠
EPF的两边分别交于点A,B和C,D。
求证:AB=CD
E
F
O
P
A
C
B
D
变式1
4已知:如图,
⊙O的弦AB,CD相交于点P,∠DPO=∠
BPO
。
求证:AB=CD
O
C
D
A
B
P
变式2
5、已知:在⊙O中,弦AB所对的劣弧为圆的1/3,圆的半径为2cm。求AB的长。
6、已知AB和CD为⊙O的两条直径,弦EC//AB,弧EC的度数为40°,求∠BOD的度数。
O
B
A
D
C
E
练习
思考
如图,已知AB、CD为
的两条弦,
,求证AB=CD.
7如图,已知AD=BC、求证AB=CD
.
O
A
B
C
D
变式:如图,如果弧AD=弧BC,求证:AB=CD
?
A
B
C
D
M
N
O
8如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM
9、如图,已知AB、CD是⊙O中互相垂直的两
条直径,又两条弦AE、CF垂直相交与点G,
试证明:AE=CF
P
.
O
A
B
C
D
┌
┐
G
E
F
O
B
A
C
D
F
E
10已知:如图,
⊙O的两条半径OA⊥OB,C、D是弧AB的三等分点。
求证:CD=AE=BF。
继续提高
11、已知:如图,
⊙O的两条直径AB⊥CD,四条弦AE//FD//CG//HB。
求证:E、F、H、G四等分圆周。
O
B
A
D
C
F
E
G
H
义务教育课程标准实验教科书
九年级
上册
人民教育出版社
24.1.3
弧、弦、圆心角
圆是中心对称图形吗?它的对称中心在哪里?
·
一、思考
圆是中心对称图形,
它的对称中心是圆心.
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
二、概念
如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.
·
O
A
B
探究
·
O
A
B
A′
B′
A′
B′
三、
因此,
重合,AB与A′B′重合.
圆心角,
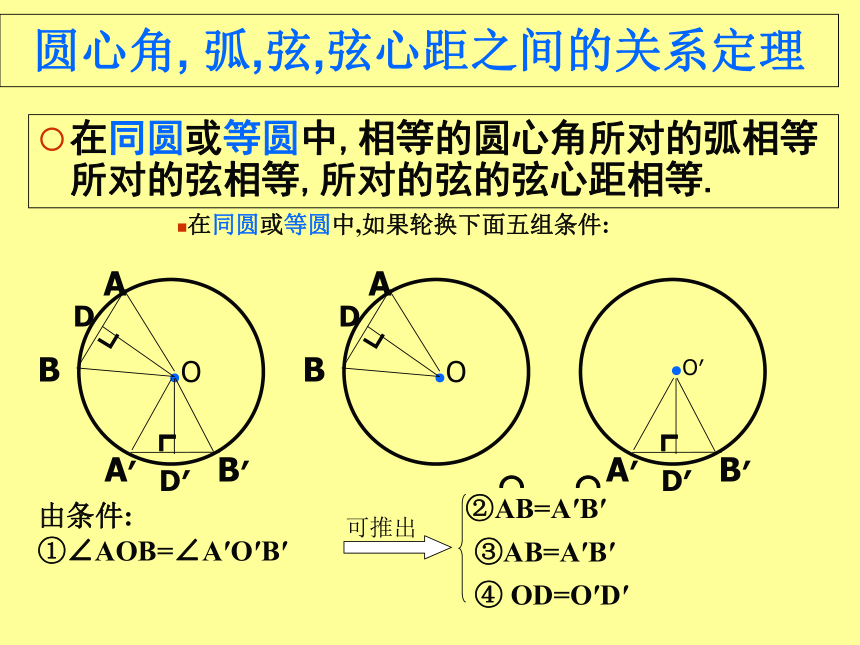
弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.
●O
A
B
A′
B′
●O
A
B
●O′
A′
B′
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
可推出
A′
B′
圆心角
圆心角
顶点在圆心的角(如∠AOB).
弦心距
过圆心作弦的垂线,圆心与垂足之间的距离(如线段OD).
如图,在⊙O中,分别作相等的圆心角和∠AOB和∠A′OB′,
将其中的一个旋转一个角度,使得OA和O′A′重合.
你能发现那些等量关系?说一说你的理由.
●O
●O
A
B
┓
D
●O
A
B
┓
D
A
B
A
B
A
B
A
B
A
B
A
B
┓
D
┓
D
┓
D
┓
D
┓
D
┓
D′
A′
B′
┓
D′
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
·
C
A
B
D
E
F
O
AB=CD
AB=CD
练习
AB=CD
⌒
⌒
⌒
⌒
AB=CD
⌒
⌒
AB=CD
圆心角,
弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
在同圆或等圆中,如果轮换下面五组条件:
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角_____,
所对的弦________,所对的弦的弦心距________
。
;
在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角______,所对的弧_________,所对的弦的弦心距________
.
这样,我们就得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,
所对的弦相等,所对的弦的弦心距也相等。
相等
相等
相等
相等
同圆或等圆中,
两个圆心角、
两条弧、两条
弦中有一组量
相等,它们所
对应的其余各
组量也相等.
四、定理
相等
相等
推论
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
①∠AOB=∠A′O′B′
?O
A
B
C
D
E
F
已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?
想一想?
1°圆心角
1°弧
C
D
n°圆心角
n°弧
把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角。1°的圆心角所对的弧叫做1°的弧。
圆心角的度数和它所对的弧的度数相等。
一般地,n°的圆心角对着n°的弧。
弧的度数
如图,AB、CD是⊙O的两条弦,
OE、OF为AB、CD的弦心距,
如果AB=CD,那么
,
,
;
如果OE=OF,那么
,
,
;
如果弧AB=弧CD,那么
,
,
;
如果∵∠AOB=∠COD,那么
,
,
。
下列说法正确吗?为什么?
在⊙O和⊙O’中,∵∠AOB=∠A’O’B’∴AB=A’B’
在⊙O和⊙O’中,∵AB=A’B’,∴弧AB=弧A’B’
注意前提:
在同圆或等圆中
O
A
B
E
C
D
F
复习回顾
证明:∵
∴
AB=AC,
△ABC等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形,AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
·
A
B
C
O
五、例题
例如图在⊙O中,
,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.
1如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
解:
练习
2已知:如图,点P在⊙O上,点O在∠EPF的平分线上,∠
EPF的两边交⊙O于点A和B。
求证:PA=PB.
E
F
A
B
P
O
基础练习
3已知:如图,点O在∠EPF的平分线上,⊙O和∠
EPF的两边分别交于点A,B和C,D。
求证:AB=CD
E
F
O
P
A
C
B
D
变式1
4已知:如图,
⊙O的弦AB,CD相交于点P,∠DPO=∠
BPO
。
求证:AB=CD
O
C
D
A
B
P
变式2
5、已知:在⊙O中,弦AB所对的劣弧为圆的1/3,圆的半径为2cm。求AB的长。
6、已知AB和CD为⊙O的两条直径,弦EC//AB,弧EC的度数为40°,求∠BOD的度数。
O
B
A
D
C
E
练习
思考
如图,已知AB、CD为
的两条弦,
,求证AB=CD.
7如图,已知AD=BC、求证AB=CD
.
O
A
B
C
D
变式:如图,如果弧AD=弧BC,求证:AB=CD
?
A
B
C
D
M
N
O
8如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM
9、如图,已知AB、CD是⊙O中互相垂直的两
条直径,又两条弦AE、CF垂直相交与点G,
试证明:AE=CF
P
.
O
A
B
C
D
┌
┐
G
E
F
O
B
A
C
D
F
E
10已知:如图,
⊙O的两条半径OA⊥OB,C、D是弧AB的三等分点。
求证:CD=AE=BF。
继续提高
11、已知:如图,
⊙O的两条直径AB⊥CD,四条弦AE//FD//CG//HB。
求证:E、F、H、G四等分圆周。
O
B
A
D
C
F
E
G
H
同课章节目录
