3.1 算式到方程(第2课时)等式的性质 课件(共30张PPT)
文档属性
| 名称 | 3.1 算式到方程(第2课时)等式的性质 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
人教版
七上
3.1算式到方程
(第2课时)
3.1.2等式的性质
教学重点:
等式的基本性质及对等式进行变形
.
教学难点:
等式的性质解简单的一元一次方程.
复习回顾
你能观察方程4x=24,
x+1=3的解吗?
x=6
x=2
你还能观察方程2x+4(x+3)=3x-(x-27)的解吗?
为了讨论解方程,我们先来看看等式有什么性质.
x=?
仅靠观察来解比较复杂的方程是困难的.
探究新知
用等号表示相等关系的式子,叫等式.
通常可以用a=b表示一般的等式.
①m+n=n+m,②x+2x=3x,
③3×3+1=5×2,④3x+1=5y
方程是含有未知数的等式.
观察下列式子有什么共同的特点?
探究新知
天平的左边
天平的右边
天平的左边=
天平的右边
天平平衡
探究新知
天平的左边=天平的右边
式子:a=b
的重量用”a”表示
的重量用”b”表示
的重量用”c”表示
天平的两边都加上
的重量.
天平的左边=天平的右边
式子:a+c=b+c
等式的两边都加同一数或式子,结果仍相等.
探究新知
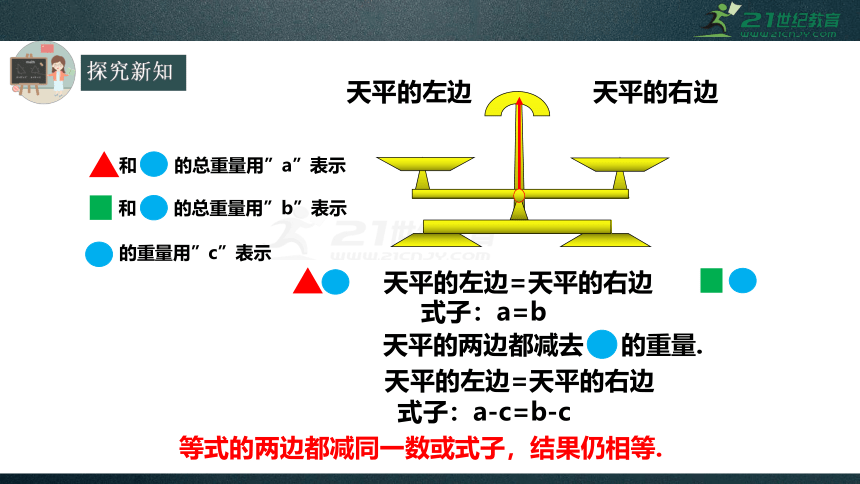
天平的左边
天平的右边
的重量用”c”表示
和
的总重量用”a”表示
和
的总重量用”b”表示
天平的左边=天平的右边
式子:a=b
天平的两边都减去
的重量.
天平的左边=天平的右边
式子:a-c=b-c
等式的两边都减同一数或式子,结果仍相等.
归纳
.
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
数学符号表示:
探究新知
天平的左边=天平的右边
式子:a=b
的重量用”a”表示
的重量用”b”表示
天平的两边扩大相同倍数(3倍)的重量.
天平的左边=天平的右边
式子:3a=3b
等式的两边都乘以同一数或式子,结果仍相等.
探究新知
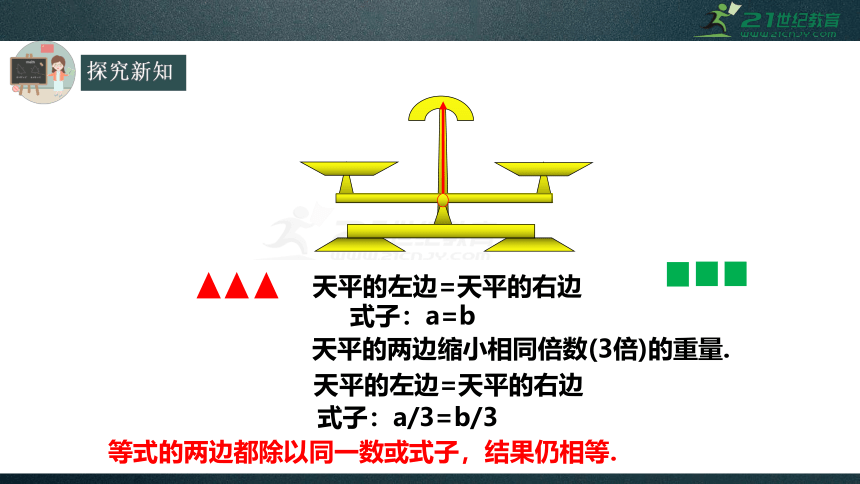
天平的左边=天平的右边
式子:a=b
天平的两边缩小相同倍数(3倍)的重量.
天平的左边=天平的右边
式子:a/3=b/3
等式的两边都除以同一数或式子,结果仍相等.
归纳
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
数学符号表示:
如果a=b(c≠0),那么
.
练一练
用适当的数或式子填空,使等式成立,并说明其变形的依据.
(1)若2a+5=3,则2a=3-
,依据是
.
(2)若3x-y=1,则3x=1+
,依据是
.
(3)若
,则x-4=
,依据是
.
等式的性质1
等式的性质1
等式的性质2
5
y
-20
归纳
用等式的性质进行等式恒等变形应注意的三点
1.等式的性质1和等式的性质2是等式恒等变形的重要依据.
2.利用等式的性质1,等式的两边必须同加或同减一个数(或式子).
3.利用等式的性质2,等式两边必须同乘或同除以一个不为0的数.
例题讲解
例2利用等式的性质解下列方程:
(1)x+7=26;
(2)-5x=20;
(3)
分析:解一元一次方程就是要将原方程转化为“
x=a
(a为常数)”的形式.需去方程左边的7,利用等式的性质1,方程两边减7就得出x的值.
解:两边减7,得
x+7-7=26-7
x=19
(等式的性质1)
例题讲解
解:
方程两边同时除以-5,得
(2)-5x=20
x=-4
(等式的性质2)
例题讲解
解:两边加5,得
方程两边同时乘以-3,得
x=-27
检验:
当x=-27时,左边=9-5=4=右边,
(等式的性质1)
所以x=-27是原方程的解.
(等式的性质2)
(3)
练一练
应用等式的性质解下列方程并检验:
(1)
x-5=
6;
(2)
0.3x
=45;
(3)
5x+4=0;
(4)
解:
(1)两边加5,得
x-5+5=6+5
于是
x=11
检验:
当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
(等式的性质1)
练一练
解:两边除以0.3,得
(2)
0.3x
=45
于是
x=150.
检验:当x=150时,左边=0.3×150=45=右边,
所以x=150是原方程的解.
(等式的性质2)
练一练
解:两边减4,得5x+4-4=0-4,得
(3)
5x+4=0
5x=-4,
两边除以5,得
检验:当
时,左边=0=右边,
(等式的性质1)
(等式的性质2)
所以
是原方程的解.
练一练
(4)
解:两边减2,得
方程两边同时乘以-4,得
x=-4
检验:
当x=-4时,左边=2-(-1)=3=右边,
所以x=-4是原方程的解.
(等式的性质1)
(等式的性质2)
归纳
利用等式的性质解简单的一元一次方程的方法
1.用等式的性质1化去方程等号左边的常数.
2.用等式的性质2把方程左边未知数的系数化为1,最终转化为x=a(常数)的形式.
3.当未知数的系数是分数时,一般两边同乘未知数系数的倒数.
课堂练习
1.下列式子中,变形正确的是(
).
A.若a=b,则2a=b+2a.
B.若3x+y=2,则3x=y+2.
C.若x=y+5,则2x=y+10.
D.若3x=-6,则x=-2.
D
2.用适当的数或式子填空,并说明其变形的依据.
(1)若2a+b=7,则2a=7
,
.
(2)若
则x=
,
.
等式的性质1
等式的性质2
-b
-5
课堂练习
3.解方程
时,应在方程两边(
).
A.两边同乘以
B.两边同乘以-3
C.两边同除以
D.两边同除以3
4.已知方程2x+1=7,那么x+1的值是(
).
A.
9
B.
7
C.
4
D.
5
B
C
课堂练习
5.应用等式的性质解下列方程并检验:
(1)
2x-3=
7;
(2)
4-5x
=9;
(3)
-2x+7=1;
(4)
解:
(1)两边加3,得
2x-3+3=7+3
于是
2x=10
检验:
当x=5时,左边=2╳5-3=7=右边,
所以x=5是原方程的解.
两边除以2,得
x=5
课堂练习
(2)
4-5x
=9
解:
两边减4,得
4-5x-4=9-4
于是
-5x=5
检验:
当x=-1时,左边=4-5╳(-1)=9=右边,
所以x=-1是原方程的解.
两边除以5,得
x=-1
课堂练习
解:两边减7,得-2x+7-7=1-7,得
(3)
-2x+7=1
-2x=-6,
两边除以-2,得
x=3,
检验:
当x=3时,左边=-2╳3+7=1=右边,
所以x=3是原方程的解.
课堂练习
(4)
检验:
当x=5时,
所以x=5是原方程的解.
解:
两边加
,得
两边乘以5,得
x=5
课堂小结
1.等式的基本性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
2.等式的基本性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
3.等式的性质解简单的一元一次方程
今天我们学习了哪些内容?
课外作业
习题3.1
第83第4题
第83第6题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
3.1算式到方程
(第2课时)
3.1.2等式的性质
教学重点:
等式的基本性质及对等式进行变形
.
教学难点:
等式的性质解简单的一元一次方程.
复习回顾
你能观察方程4x=24,
x+1=3的解吗?
x=6
x=2
你还能观察方程2x+4(x+3)=3x-(x-27)的解吗?
为了讨论解方程,我们先来看看等式有什么性质.
x=?
仅靠观察来解比较复杂的方程是困难的.
探究新知
用等号表示相等关系的式子,叫等式.
通常可以用a=b表示一般的等式.
①m+n=n+m,②x+2x=3x,
③3×3+1=5×2,④3x+1=5y
方程是含有未知数的等式.
观察下列式子有什么共同的特点?
探究新知
天平的左边
天平的右边
天平的左边=
天平的右边
天平平衡
探究新知
天平的左边=天平的右边
式子:a=b
的重量用”a”表示
的重量用”b”表示
的重量用”c”表示
天平的两边都加上
的重量.
天平的左边=天平的右边
式子:a+c=b+c
等式的两边都加同一数或式子,结果仍相等.
探究新知
天平的左边
天平的右边
的重量用”c”表示
和
的总重量用”a”表示
和
的总重量用”b”表示
天平的左边=天平的右边
式子:a=b
天平的两边都减去
的重量.
天平的左边=天平的右边
式子:a-c=b-c
等式的两边都减同一数或式子,结果仍相等.
归纳
.
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
数学符号表示:
探究新知
天平的左边=天平的右边
式子:a=b
的重量用”a”表示
的重量用”b”表示
天平的两边扩大相同倍数(3倍)的重量.
天平的左边=天平的右边
式子:3a=3b
等式的两边都乘以同一数或式子,结果仍相等.
探究新知
天平的左边=天平的右边
式子:a=b
天平的两边缩小相同倍数(3倍)的重量.
天平的左边=天平的右边
式子:a/3=b/3
等式的两边都除以同一数或式子,结果仍相等.
归纳
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
数学符号表示:
如果a=b(c≠0),那么
.
练一练
用适当的数或式子填空,使等式成立,并说明其变形的依据.
(1)若2a+5=3,则2a=3-
,依据是
.
(2)若3x-y=1,则3x=1+
,依据是
.
(3)若
,则x-4=
,依据是
.
等式的性质1
等式的性质1
等式的性质2
5
y
-20
归纳
用等式的性质进行等式恒等变形应注意的三点
1.等式的性质1和等式的性质2是等式恒等变形的重要依据.
2.利用等式的性质1,等式的两边必须同加或同减一个数(或式子).
3.利用等式的性质2,等式两边必须同乘或同除以一个不为0的数.
例题讲解
例2利用等式的性质解下列方程:
(1)x+7=26;
(2)-5x=20;
(3)
分析:解一元一次方程就是要将原方程转化为“
x=a
(a为常数)”的形式.需去方程左边的7,利用等式的性质1,方程两边减7就得出x的值.
解:两边减7,得
x+7-7=26-7
x=19
(等式的性质1)
例题讲解
解:
方程两边同时除以-5,得
(2)-5x=20
x=-4
(等式的性质2)
例题讲解
解:两边加5,得
方程两边同时乘以-3,得
x=-27
检验:
当x=-27时,左边=9-5=4=右边,
(等式的性质1)
所以x=-27是原方程的解.
(等式的性质2)
(3)
练一练
应用等式的性质解下列方程并检验:
(1)
x-5=
6;
(2)
0.3x
=45;
(3)
5x+4=0;
(4)
解:
(1)两边加5,得
x-5+5=6+5
于是
x=11
检验:
当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
(等式的性质1)
练一练
解:两边除以0.3,得
(2)
0.3x
=45
于是
x=150.
检验:当x=150时,左边=0.3×150=45=右边,
所以x=150是原方程的解.
(等式的性质2)
练一练
解:两边减4,得5x+4-4=0-4,得
(3)
5x+4=0
5x=-4,
两边除以5,得
检验:当
时,左边=0=右边,
(等式的性质1)
(等式的性质2)
所以
是原方程的解.
练一练
(4)
解:两边减2,得
方程两边同时乘以-4,得
x=-4
检验:
当x=-4时,左边=2-(-1)=3=右边,
所以x=-4是原方程的解.
(等式的性质1)
(等式的性质2)
归纳
利用等式的性质解简单的一元一次方程的方法
1.用等式的性质1化去方程等号左边的常数.
2.用等式的性质2把方程左边未知数的系数化为1,最终转化为x=a(常数)的形式.
3.当未知数的系数是分数时,一般两边同乘未知数系数的倒数.
课堂练习
1.下列式子中,变形正确的是(
).
A.若a=b,则2a=b+2a.
B.若3x+y=2,则3x=y+2.
C.若x=y+5,则2x=y+10.
D.若3x=-6,则x=-2.
D
2.用适当的数或式子填空,并说明其变形的依据.
(1)若2a+b=7,则2a=7
,
.
(2)若
则x=
,
.
等式的性质1
等式的性质2
-b
-5
课堂练习
3.解方程
时,应在方程两边(
).
A.两边同乘以
B.两边同乘以-3
C.两边同除以
D.两边同除以3
4.已知方程2x+1=7,那么x+1的值是(
).
A.
9
B.
7
C.
4
D.
5
B
C
课堂练习
5.应用等式的性质解下列方程并检验:
(1)
2x-3=
7;
(2)
4-5x
=9;
(3)
-2x+7=1;
(4)
解:
(1)两边加3,得
2x-3+3=7+3
于是
2x=10
检验:
当x=5时,左边=2╳5-3=7=右边,
所以x=5是原方程的解.
两边除以2,得
x=5
课堂练习
(2)
4-5x
=9
解:
两边减4,得
4-5x-4=9-4
于是
-5x=5
检验:
当x=-1时,左边=4-5╳(-1)=9=右边,
所以x=-1是原方程的解.
两边除以5,得
x=-1
课堂练习
解:两边减7,得-2x+7-7=1-7,得
(3)
-2x+7=1
-2x=-6,
两边除以-2,得
x=3,
检验:
当x=3时,左边=-2╳3+7=1=右边,
所以x=3是原方程的解.
课堂练习
(4)
检验:
当x=5时,
所以x=5是原方程的解.
解:
两边加
,得
两边乘以5,得
x=5
课堂小结
1.等式的基本性质1:
等式两边加(或减)同一个数(或式子),结果仍相等.
2.等式的基本性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
3.等式的性质解简单的一元一次方程
今天我们学习了哪些内容?
课外作业
习题3.1
第83第4题
第83第6题
https://www.21cnjy.com/help/help_extract.php
