苏科版七年级数学上册 第6章 平面图形的认识(一) 单元检测试题(Word版 含解析)
文档属性
| 名称 | 苏科版七年级数学上册 第6章 平面图形的认识(一) 单元检测试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 109.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 09:32:17 | ||
图片预览


文档简介
1049020010693400123190000第6章 平面图形的认识(一) 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列说法正确的是( )
A.若MA=MB,则M是线段AB的中点
B.直线比射线长,射线比线段长
C.线段BA与线段AB表示同一条线段
D.射线OA和射线AO是同一条射线
?
2. 如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
A.6 B.9 C.12 D.18
?
3. 在同一平面内,已知线段AB的长为10厘米,点A、B到直线l的距离分别为6厘米和4厘米,则符合条件的直线l的条数为( )
A.2条 B.3条 C.4条 D.无数条
?
4. 过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
?
5. 如图所示,OC,OD分别是∠AOB,∠AOC的平分线,且∠COD=25?,则∠AOB为( )
A.100? B.120? C.135? D.150?
?
6. 以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A.②③ B.③ C.①② D.①
?
7. 下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
?
8. 点E在线段CD上,下面的等式:①CE=DE;②DE=12CD;③CD=2CE;④CD=12DE.其中能表示E是CD中点的有( )
A.1个 B.2个 C.3个 D.4个
?
9. 如图,已知线段AB=3cm,延长AB到C,使BC=6?cm,又延长BA到D,使DA=1?cm,下列结论正确的是( )
A.DB=23BC B.DC=25AB C.DA=14AB D.DB=34AB
?
10. 下列各式计算正确的是( )
A.12?=118″ B.38゜15'=38.15゜
C.24.8゜×2=49.6゜ D.90゜-85゜45'=4゜65'
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图所示,点A,O,B在同一条直线上,其中小于180?的角共有________个.
?
12. 计算:①33?52'+21?54'=________;②36?27'×3=________.
?
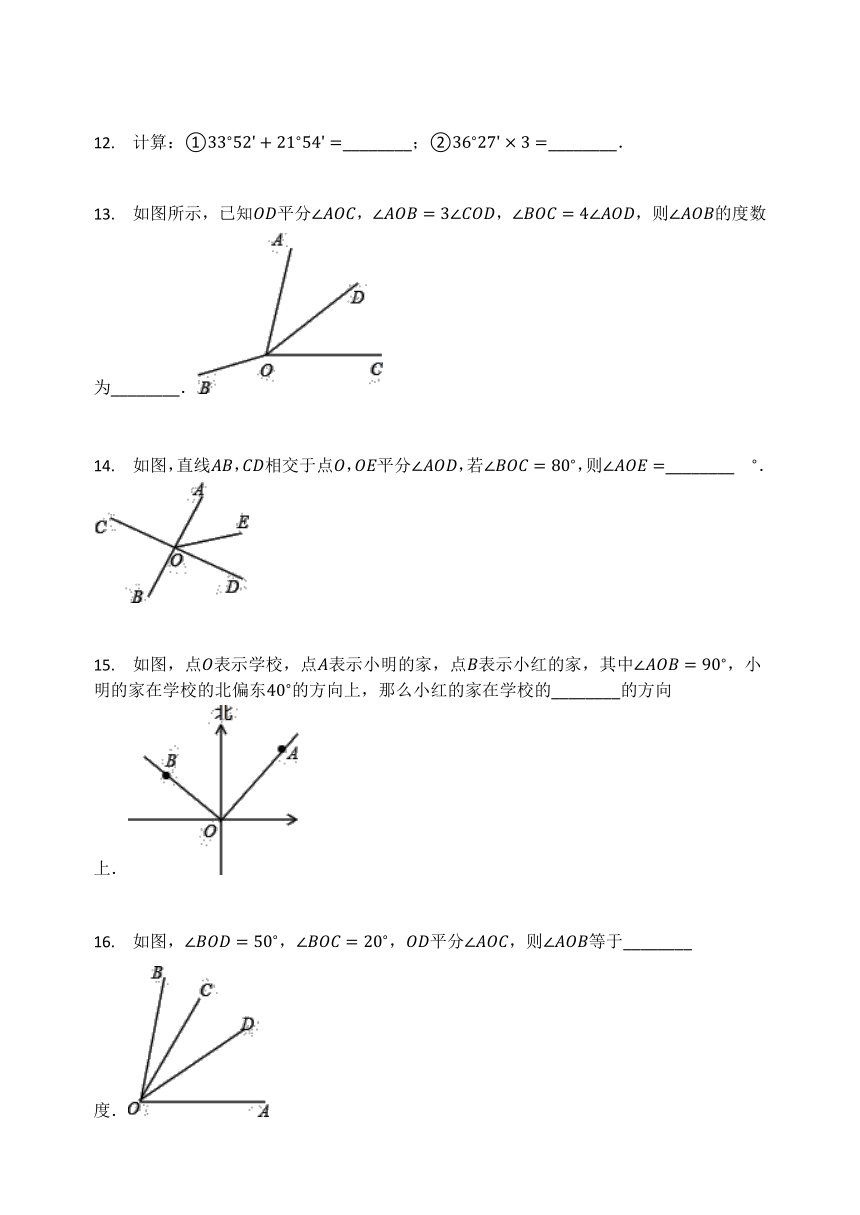
13. 如图所示,已知OD平分∠AOC,∠AOB=3∠COD,∠BOC=4∠AOD,则∠AOB的度数为________.
?
14. 如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOC=80?,则∠AOE=________??.
?
15. 如图,点O表示学校,点A表示小明的家,点B表示小红的家,其中∠AOB=90?,小明的家在学校的北偏东40?的方向上,那么小红的家在学校的________的方向上.
?
16. 如图,∠BOD=50?,∠BOC=20?,OD平分∠AOC,则∠AOB等于________度.
?
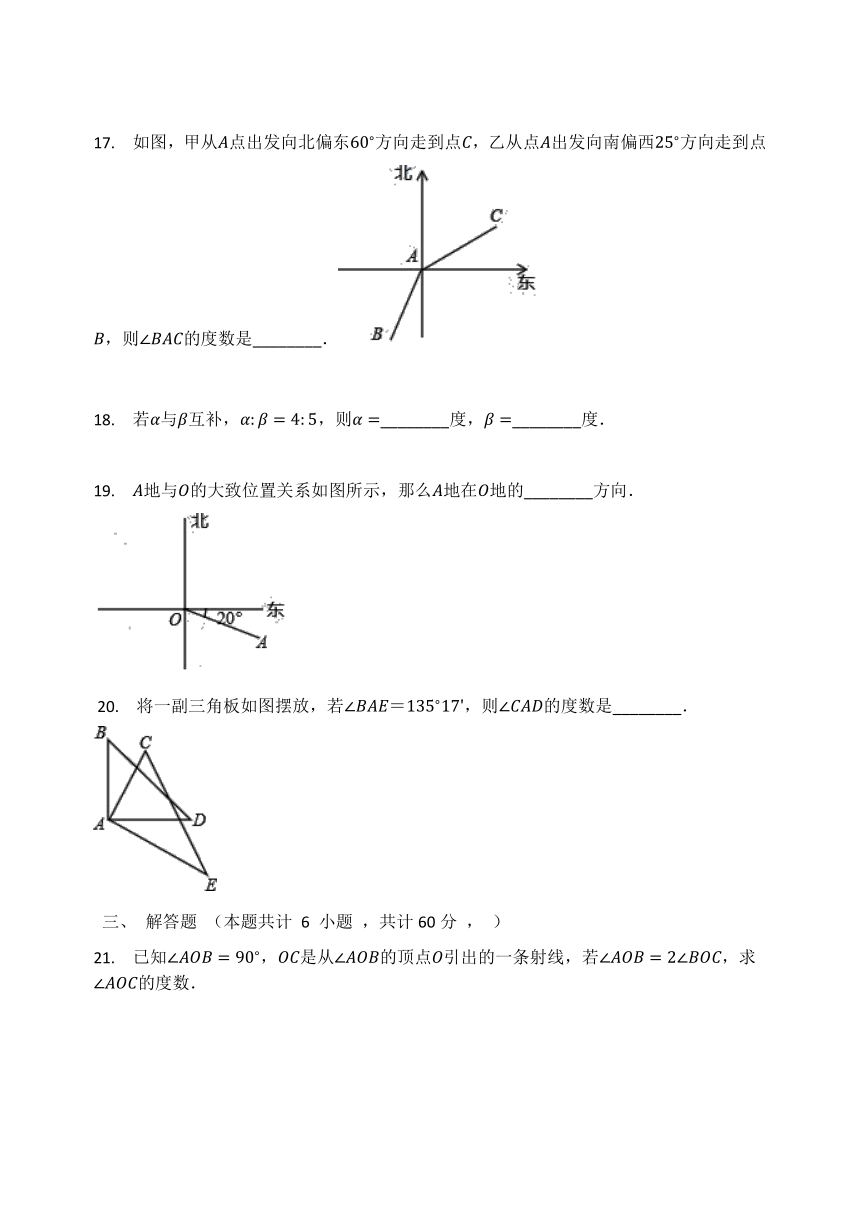
17. 如图,甲从A点出发向北偏东60?方向走到点C,乙从点A出发向南偏西25?方向走到点B,则∠BAC的度数是________.
?
18. 若α与β互补,α:β=4:5,则α=________度,β=________度.
?
19. A地与O的大致位置关系如图所示,那么A地在O地的________方向.
?20. 将一副三角板如图摆放,若∠BAE=135?17',则∠CAD的度数是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 已知∠AOB=90?,OC是从∠AOB的顶点O引出的一条射线,若∠AOB=2∠BOC,求∠AOC的度数.
?
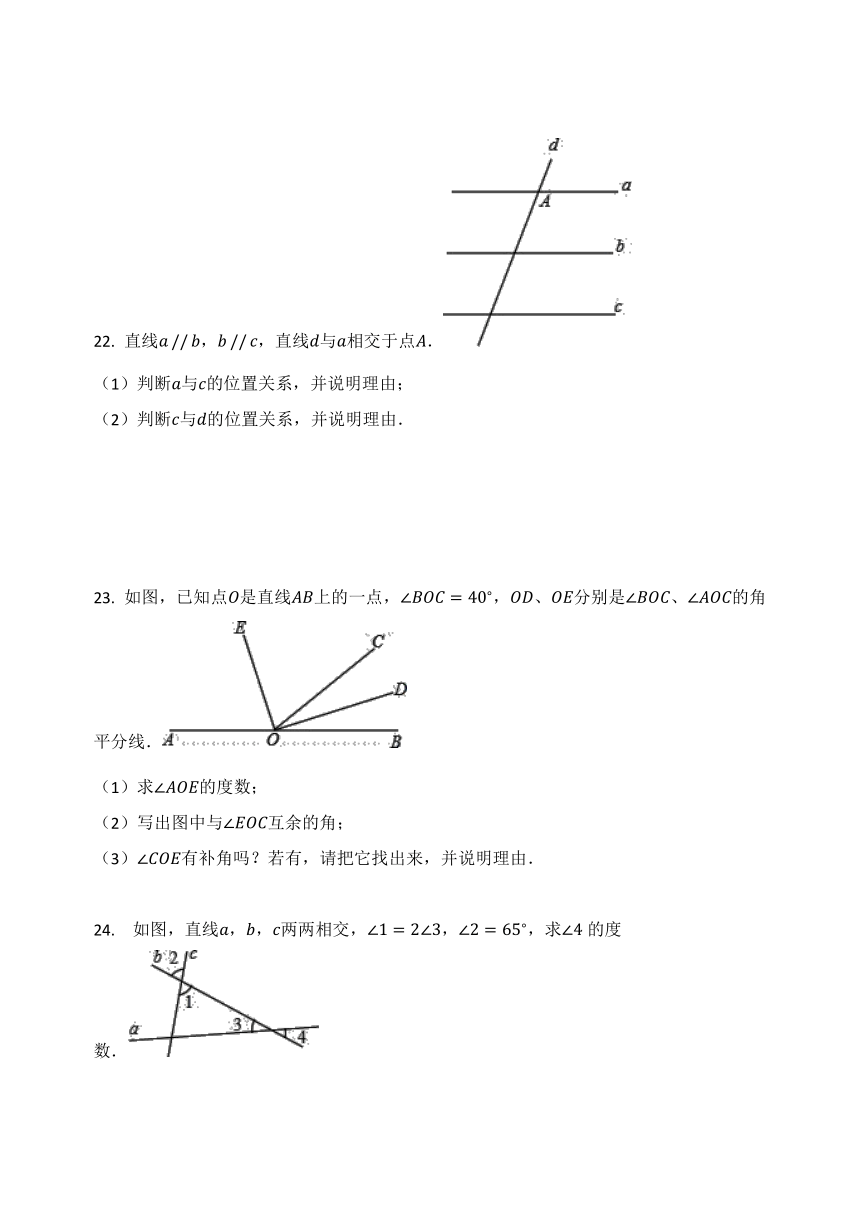
22. 直线a?//?b,b?//?c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;?
(2)判断c与d的位置关系,并说明理由.
?
23. 如图,已知点O是直线AB上的一点,∠BOC=40?,OD、OE分别是∠BOC、∠AOC的角平分线.
(1)求∠AOE的度数;
(2)写出图中与∠EOC互余的角;
(3)∠COE有补角吗?若有,请把它找出来,并说明理由.
?
24. 如图,直线a,b,c两两相交,∠1=2∠3,∠2=65?,求∠4的度数.
?
25. 已知:如图,直线a、b、c两两相交,∠1=2∠3,∠2=86?.求∠4的度数.
?
26. 探索与发现:
(1)若直线a1⊥a2,a2?//?a3,则直线a1与a3的位置关系是________,请说明理由.
(2)若直线a1⊥a2,a2?//?a3,a3⊥a4,则直线a1与a4的位置关系是________(直接填结论,不需要证明)
(3)现在有2020条直线a1,a2,a3,…,a2020,且有a1⊥a2,a2?//?a3,a3⊥a4,a4?//?a5…,请你探索直线a1与a2020的位置关系.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【解析】
本题需先根据直线、射线、线段的定义以及表示方法,分别进行判断即可求出答案.
【解答】
A、MA=MB,M不一定是线段AB的中点,故本选项错误;
B、∵ 直线与射线不能比较长短,故本选项错误;
C、线段BA与线段AB表示同一条线段,故本选项正确;
D、射线OA和射线AO不是同一条射线,故本选项错误;
2.
【解析】
根据线段的中点的定义得出ED=12(AC+BC)=12AB,即可求出AB的长.
【解答】
∵ 点E是AC中点,点D是BC中点,
∴ AE=CE=12AC,CD=BD=12BC,
∴ CE+CD=12AC+12BC,
即ED=12(AC+BC)=12AB,
∴ AB=2ED=12;
3.
【解析】
根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.画出图形进行判断.
【解答】
解:①如图1,
在线段AB的两旁可分别画一条满足条件的直线;
②作线段AB的垂线,将线段AB分成6cm,4cm两部分.
故选:B.
4.
【解析】
分三点共线和不共线两种情况作出图形,即可得解.
【解答】
解:如图,过平面上A、B、C三点中的任意两点作直线,可作1条或3条.
故选C.
5.
【解析】
利用角的平分线的性质计算.
【解答】
解:∵ OD为∠AOC的平分线
∴ ∠AOD=∠COD=25?
∴ ∠AOC=50?
又∵ OC为∠AOB的平分线
∴ ∠AOB=100?
故选A.
6.
【解析】
根据线段的概念,直线的性质和余角、补角的定义进行判断.
【解答】
解:①在同一直线上的4点A、B、C、D只能表示6条不同的线段,故错误;
②经过两点有一条直线,并且只有一条直线,正确;
③同一个锐角的补角一定大于它的余角,正确.
故选A.
7.
【解析】
根据相关的定义或定理,逐一判断,排除错误答案.
【解答】
(2)如果两条线段没有交点,那么这两条线段所在直线不一定没有交点,故(2)错误(1)(3)邻补角的两条角平分线一定构成一个直角,故(3)正确(2)(4)同一平面内,过一点有且只有一条直线与已知直线垂直,故(4)正确(3)(5)同一平面内,过直线外一点有且只有一条直线与已知直线平行,故(5)错误.
其中正确的是2个.
故选:B.
8.
【解析】
点E如果是线段CD的中点,则点E将线段CD分成两段长度相等的线段.即:CE=DE.由此性质可判断出哪一项符合要求.
【解答】
解:假设点E是线段CD的中点,则CE=DE,故①正确;
当DE=12CD时,则CE=12CD,点E是线段CD的中点,故②正确;
当CD=2CE,则DE=2CE-CE=CE,点E是线段CD的中点,故③正确;
④CD=12DE,点E不是线段CD的中点,故④不正确;
综上所述:①、②、③正确,只有④是错误的.
故选:C.
9.
【解析】
由已知关系,我们可以求出各线段的长度,即DB=4cm,DC=10cm,所以有DB=23BC,DC=103AB,DA=13AB,DB=43AB.经过比较可知,答案选择A.
【解答】
解:由已知,AB=3cm,BC=6?cm,DA=1?cm;
所以有DB=4cm,DC=10cm,
即有DB=23BC,DC=103AB;
DA=13AB,DB=43AB.
综上所述,故选A.
10.
【解析】
根据1?=60',1'=60″,结合各选项进行判断即可.
【解答】
解:A、12?=30',故本选项错误;
B、38゜15'=38.25゜,故本选项错误;
C、24.8゜×2=49.6゜,计算正确,故本选项正确;
D、90゜-85゜45'=4゜15',故本选项错误;
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【解析】
根据角是由公共顶点的两条射线组成的图形,可得答案.
【解答】
解:图中的角有∠AOC,∠AOD,∠AOE,∠COD,∠COE,∠COB,∠DOE,∠DOB,∠EOB,
故答案为:9.
12.
【解析】
①利用度加度,分加分,再进位即可;②利用度和分分别乘以3,再进位.
【解答】
解:①33?52'+21?54'=54?106'=55?46';
②36?27'×3=108?81'=109?21';
故答案为:55?46';109?21'.
13.
【解析】
根据角平分线的性质,可得∠COD与∠AOD的关系,根据角的和差,可得∠COD的度数,根据∠AOB=3∠COD,可得答案.
【解答】
解:由OD平分∠AOC,得
∠AOC=2∠AOD=2∠COD,∠BOC=4∠AOD=4∠COD.
由角的和差,得
∠AOC+∠AOB+∠BOC=360?,
即2∠COD+3∠COD+4∠COD=360?.
解得∠COD=40?,
∠AOB=3∠COD=3×40?=120?,
故答案为:120?.
14.
【解析】
根据对顶角相等可得∠AOD=80?,再根据角平分线的性质可得∠AOE的度数.
【解答】
解:∵ ∠BOC=80?,
∴ ∠AOD=80?,
∵ OE平分∠AOD,
∴ ∠AOE=80?÷2=40?,
故答案为:40.
15.
【解析】
由∠1=40?,利用余角的定义可得∠2=50?,即可得出小红的家在学校的方向.
【解答】
解:如图,
∵ ∠AOB=90?,∠1=40?,
∴ ∠2=90?-40?=50?,
∴ 小红的家在学校的北偏西50?的方向上.
故答案为:北偏西50?.
16.
【解析】
先求出∠DOC,根据角平分线定义求出∠AOC,即可求出答案.
【解答】
解:∵ ∠BOD=50?,∠BOC=20?,
∴ ∠DOC=∠BOD-∠BOC=30?,
∵ OD平分∠AOC,
∴ ∠AOC=2∠OC=60?,
∴ ∠AOB=∠AOC+∠BOC=60?+20?=80?,
故答案为:80.
17.
【解析】
∠BAC等于三个角的和,求出各角的度数,相加即可.
【解答】
解:如图,
由题意,可知:∠AOD=60?,
∴ ∠CAE=30?,
∵ ∠BAF=25?,
∴ ∠BAC=∠CAE+∠EAF+∠BAF
=30?+90?+25?
=145?,
故答案为:145?.
18.
【解析】
根据余角和补角的概念以及题意可知.
【解答】
解:α+β=180?,α:β=4:5,
所以可设α=4x,β=5x,
则4x+5x=180,
解得x=20,
故α=80?,β=100?.
19.
【解析】
方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.依此即可求解.
【解答】
观察图形可知,A地在O地的南偏东90?-20?=70?方向.
20.
【解析】
利用三角形的各角度数和图中角与角的关系计算.
【解答】
∠BAE=∠BAD+∠CAE-∠CAD
则∠CAD=∠BAD+∠CAE-∠BAE=90+90-∠BAE=44?43'.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【解析】
根据题意可知:∠BOC=45?,由于题目没有说明OC是∠AOB的内部还是外部,故要分情况讨论.
【解答】
解:由题意可知:∠BOC=45?,
当OC在∠AOB的内部时,
∴ ∠AOC=∠AOB-∠BOC=90?-45?=45?
当OC在∠AOB的外部时,
∴ ∠AOC=∠AOB+∠BOC=135?
综上所述,∠AOC的度数为45?或135?
22.
【解析】
(1)根据平行公理得出即可;
(2)根据c?//?a和直线d与a相交推出即可.
【解答】
解:(1)a与c的位置关系是平行,
理由是:∵ 直线a?//?b,b?//?c,
∴ a?//?c;
(2)c与d的位置关系是相交,
理由是:∵ c?//?a,直线d与a相交于点A,
∴ c与d的位置关系是相交.
23.
【解析】
(1)利用角平分线的性质以及互补的定义得出即可;
(2)利用角平分线的性质以及互余的定义得出即可;
(3)利用角平分线的性质以及互补的定义得出即可.
【解答】
解:(1)∵ ∠BOC=40?,
∴ ∠AOC=140?,
∵ OE是∠AOC的角平分线,
∴ ∠AOE的度数为:140?÷2=70?;
(2)∵ OD、OE分别是∠BOC、∠AOC的角平分线,
∴ ∠AOE=∠EOC,∠COD=∠BOD,
∴ ∠EOC+∠COD=90?,
∴ ∠BOD+∠EOC=90?,
∴ 图中与∠EOC互余的角有∠COD,∠BOD;
(3)∠COE有补角,
理由:∵ ∠AOE=∠EOC,∠AOE+∠BOE=180?,
∴ ∠COE+∠BOE=180?,
∴ ∠COE有补角是∠BOE.
24.
【解析】
结合∠1=2∠3,利用对顶角相等的性质求出∠3的度数,再求∠4的度数.
【解答】
解:根据对顶角相等,得∠1=∠2=65?,
∵ ∠1=2∠3,
∴ ∠3=32.5?,
∴ ∠4=∠3=32.5?.
25.
【解析】
结合∠1=2∠3,利用对顶角相等的性质求出∠3的度数,再求∠4的度数.
【解答】
解:根据对顶角相等,得∠1=∠2=86?,
∵ ∠1=2∠3,
∴ ∠3=43?,
∴ ∠4=∠3=43?.
26.
【解析】
(1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;
(2)根据(1)中结论即可判定垂直;
(3)根据规律发现,与脚码是偶数的直线互相平行,与脚码是奇数的直线互相垂直,根据此规律即可判断.
【解答】
解:(1)a1⊥a3.
理由如下:如图1,∵ a1⊥a2,
∴ ∠1=90?,
∵ a2?//?a3,
∴ ∠2=∠1=90?,
∴ a1⊥a3;
(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1?//?a4;
(3)直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1?//?a4,
以此类推,直线a1与a2020的位置关系是:a1⊥a2020.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列说法正确的是( )
A.若MA=MB,则M是线段AB的中点
B.直线比射线长,射线比线段长
C.线段BA与线段AB表示同一条线段
D.射线OA和射线AO是同一条射线
?
2. 如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
A.6 B.9 C.12 D.18
?
3. 在同一平面内,已知线段AB的长为10厘米,点A、B到直线l的距离分别为6厘米和4厘米,则符合条件的直线l的条数为( )
A.2条 B.3条 C.4条 D.无数条
?
4. 过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
?
5. 如图所示,OC,OD分别是∠AOB,∠AOC的平分线,且∠COD=25?,则∠AOB为( )
A.100? B.120? C.135? D.150?
?
6. 以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A.②③ B.③ C.①② D.①
?
7. 下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
?
8. 点E在线段CD上,下面的等式:①CE=DE;②DE=12CD;③CD=2CE;④CD=12DE.其中能表示E是CD中点的有( )
A.1个 B.2个 C.3个 D.4个
?
9. 如图,已知线段AB=3cm,延长AB到C,使BC=6?cm,又延长BA到D,使DA=1?cm,下列结论正确的是( )
A.DB=23BC B.DC=25AB C.DA=14AB D.DB=34AB
?
10. 下列各式计算正确的是( )
A.12?=118″ B.38゜15'=38.15゜
C.24.8゜×2=49.6゜ D.90゜-85゜45'=4゜65'
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图所示,点A,O,B在同一条直线上,其中小于180?的角共有________个.
?
12. 计算:①33?52'+21?54'=________;②36?27'×3=________.
?
13. 如图所示,已知OD平分∠AOC,∠AOB=3∠COD,∠BOC=4∠AOD,则∠AOB的度数为________.
?
14. 如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOC=80?,则∠AOE=________??.
?
15. 如图,点O表示学校,点A表示小明的家,点B表示小红的家,其中∠AOB=90?,小明的家在学校的北偏东40?的方向上,那么小红的家在学校的________的方向上.
?
16. 如图,∠BOD=50?,∠BOC=20?,OD平分∠AOC,则∠AOB等于________度.
?
17. 如图,甲从A点出发向北偏东60?方向走到点C,乙从点A出发向南偏西25?方向走到点B,则∠BAC的度数是________.
?
18. 若α与β互补,α:β=4:5,则α=________度,β=________度.
?
19. A地与O的大致位置关系如图所示,那么A地在O地的________方向.
?20. 将一副三角板如图摆放,若∠BAE=135?17',则∠CAD的度数是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 已知∠AOB=90?,OC是从∠AOB的顶点O引出的一条射线,若∠AOB=2∠BOC,求∠AOC的度数.
?
22. 直线a?//?b,b?//?c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;?
(2)判断c与d的位置关系,并说明理由.
?
23. 如图,已知点O是直线AB上的一点,∠BOC=40?,OD、OE分别是∠BOC、∠AOC的角平分线.
(1)求∠AOE的度数;
(2)写出图中与∠EOC互余的角;
(3)∠COE有补角吗?若有,请把它找出来,并说明理由.
?
24. 如图,直线a,b,c两两相交,∠1=2∠3,∠2=65?,求∠4的度数.
?
25. 已知:如图,直线a、b、c两两相交,∠1=2∠3,∠2=86?.求∠4的度数.
?
26. 探索与发现:
(1)若直线a1⊥a2,a2?//?a3,则直线a1与a3的位置关系是________,请说明理由.
(2)若直线a1⊥a2,a2?//?a3,a3⊥a4,则直线a1与a4的位置关系是________(直接填结论,不需要证明)
(3)现在有2020条直线a1,a2,a3,…,a2020,且有a1⊥a2,a2?//?a3,a3⊥a4,a4?//?a5…,请你探索直线a1与a2020的位置关系.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【解析】
本题需先根据直线、射线、线段的定义以及表示方法,分别进行判断即可求出答案.
【解答】
A、MA=MB,M不一定是线段AB的中点,故本选项错误;
B、∵ 直线与射线不能比较长短,故本选项错误;
C、线段BA与线段AB表示同一条线段,故本选项正确;
D、射线OA和射线AO不是同一条射线,故本选项错误;
2.
【解析】
根据线段的中点的定义得出ED=12(AC+BC)=12AB,即可求出AB的长.
【解答】
∵ 点E是AC中点,点D是BC中点,
∴ AE=CE=12AC,CD=BD=12BC,
∴ CE+CD=12AC+12BC,
即ED=12(AC+BC)=12AB,
∴ AB=2ED=12;
3.
【解析】
根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.画出图形进行判断.
【解答】
解:①如图1,
在线段AB的两旁可分别画一条满足条件的直线;
②作线段AB的垂线,将线段AB分成6cm,4cm两部分.
故选:B.
4.
【解析】
分三点共线和不共线两种情况作出图形,即可得解.
【解答】
解:如图,过平面上A、B、C三点中的任意两点作直线,可作1条或3条.
故选C.
5.
【解析】
利用角的平分线的性质计算.
【解答】
解:∵ OD为∠AOC的平分线
∴ ∠AOD=∠COD=25?
∴ ∠AOC=50?
又∵ OC为∠AOB的平分线
∴ ∠AOB=100?
故选A.
6.
【解析】
根据线段的概念,直线的性质和余角、补角的定义进行判断.
【解答】
解:①在同一直线上的4点A、B、C、D只能表示6条不同的线段,故错误;
②经过两点有一条直线,并且只有一条直线,正确;
③同一个锐角的补角一定大于它的余角,正确.
故选A.
7.
【解析】
根据相关的定义或定理,逐一判断,排除错误答案.
【解答】
(2)如果两条线段没有交点,那么这两条线段所在直线不一定没有交点,故(2)错误(1)(3)邻补角的两条角平分线一定构成一个直角,故(3)正确(2)(4)同一平面内,过一点有且只有一条直线与已知直线垂直,故(4)正确(3)(5)同一平面内,过直线外一点有且只有一条直线与已知直线平行,故(5)错误.
其中正确的是2个.
故选:B.
8.
【解析】
点E如果是线段CD的中点,则点E将线段CD分成两段长度相等的线段.即:CE=DE.由此性质可判断出哪一项符合要求.
【解答】
解:假设点E是线段CD的中点,则CE=DE,故①正确;
当DE=12CD时,则CE=12CD,点E是线段CD的中点,故②正确;
当CD=2CE,则DE=2CE-CE=CE,点E是线段CD的中点,故③正确;
④CD=12DE,点E不是线段CD的中点,故④不正确;
综上所述:①、②、③正确,只有④是错误的.
故选:C.
9.
【解析】
由已知关系,我们可以求出各线段的长度,即DB=4cm,DC=10cm,所以有DB=23BC,DC=103AB,DA=13AB,DB=43AB.经过比较可知,答案选择A.
【解答】
解:由已知,AB=3cm,BC=6?cm,DA=1?cm;
所以有DB=4cm,DC=10cm,
即有DB=23BC,DC=103AB;
DA=13AB,DB=43AB.
综上所述,故选A.
10.
【解析】
根据1?=60',1'=60″,结合各选项进行判断即可.
【解答】
解:A、12?=30',故本选项错误;
B、38゜15'=38.25゜,故本选项错误;
C、24.8゜×2=49.6゜,计算正确,故本选项正确;
D、90゜-85゜45'=4゜15',故本选项错误;
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【解析】
根据角是由公共顶点的两条射线组成的图形,可得答案.
【解答】
解:图中的角有∠AOC,∠AOD,∠AOE,∠COD,∠COE,∠COB,∠DOE,∠DOB,∠EOB,
故答案为:9.
12.
【解析】
①利用度加度,分加分,再进位即可;②利用度和分分别乘以3,再进位.
【解答】
解:①33?52'+21?54'=54?106'=55?46';
②36?27'×3=108?81'=109?21';
故答案为:55?46';109?21'.
13.
【解析】
根据角平分线的性质,可得∠COD与∠AOD的关系,根据角的和差,可得∠COD的度数,根据∠AOB=3∠COD,可得答案.
【解答】
解:由OD平分∠AOC,得
∠AOC=2∠AOD=2∠COD,∠BOC=4∠AOD=4∠COD.
由角的和差,得
∠AOC+∠AOB+∠BOC=360?,
即2∠COD+3∠COD+4∠COD=360?.
解得∠COD=40?,
∠AOB=3∠COD=3×40?=120?,
故答案为:120?.
14.
【解析】
根据对顶角相等可得∠AOD=80?,再根据角平分线的性质可得∠AOE的度数.
【解答】
解:∵ ∠BOC=80?,
∴ ∠AOD=80?,
∵ OE平分∠AOD,
∴ ∠AOE=80?÷2=40?,
故答案为:40.
15.
【解析】
由∠1=40?,利用余角的定义可得∠2=50?,即可得出小红的家在学校的方向.
【解答】
解:如图,
∵ ∠AOB=90?,∠1=40?,
∴ ∠2=90?-40?=50?,
∴ 小红的家在学校的北偏西50?的方向上.
故答案为:北偏西50?.
16.
【解析】
先求出∠DOC,根据角平分线定义求出∠AOC,即可求出答案.
【解答】
解:∵ ∠BOD=50?,∠BOC=20?,
∴ ∠DOC=∠BOD-∠BOC=30?,
∵ OD平分∠AOC,
∴ ∠AOC=2∠OC=60?,
∴ ∠AOB=∠AOC+∠BOC=60?+20?=80?,
故答案为:80.
17.
【解析】
∠BAC等于三个角的和,求出各角的度数,相加即可.
【解答】
解:如图,
由题意,可知:∠AOD=60?,
∴ ∠CAE=30?,
∵ ∠BAF=25?,
∴ ∠BAC=∠CAE+∠EAF+∠BAF
=30?+90?+25?
=145?,
故答案为:145?.
18.
【解析】
根据余角和补角的概念以及题意可知.
【解答】
解:α+β=180?,α:β=4:5,
所以可设α=4x,β=5x,
则4x+5x=180,
解得x=20,
故α=80?,β=100?.
19.
【解析】
方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.依此即可求解.
【解答】
观察图形可知,A地在O地的南偏东90?-20?=70?方向.
20.
【解析】
利用三角形的各角度数和图中角与角的关系计算.
【解答】
∠BAE=∠BAD+∠CAE-∠CAD
则∠CAD=∠BAD+∠CAE-∠BAE=90+90-∠BAE=44?43'.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【解析】
根据题意可知:∠BOC=45?,由于题目没有说明OC是∠AOB的内部还是外部,故要分情况讨论.
【解答】
解:由题意可知:∠BOC=45?,
当OC在∠AOB的内部时,
∴ ∠AOC=∠AOB-∠BOC=90?-45?=45?
当OC在∠AOB的外部时,
∴ ∠AOC=∠AOB+∠BOC=135?
综上所述,∠AOC的度数为45?或135?
22.
【解析】
(1)根据平行公理得出即可;
(2)根据c?//?a和直线d与a相交推出即可.
【解答】
解:(1)a与c的位置关系是平行,
理由是:∵ 直线a?//?b,b?//?c,
∴ a?//?c;
(2)c与d的位置关系是相交,
理由是:∵ c?//?a,直线d与a相交于点A,
∴ c与d的位置关系是相交.
23.
【解析】
(1)利用角平分线的性质以及互补的定义得出即可;
(2)利用角平分线的性质以及互余的定义得出即可;
(3)利用角平分线的性质以及互补的定义得出即可.
【解答】
解:(1)∵ ∠BOC=40?,
∴ ∠AOC=140?,
∵ OE是∠AOC的角平分线,
∴ ∠AOE的度数为:140?÷2=70?;
(2)∵ OD、OE分别是∠BOC、∠AOC的角平分线,
∴ ∠AOE=∠EOC,∠COD=∠BOD,
∴ ∠EOC+∠COD=90?,
∴ ∠BOD+∠EOC=90?,
∴ 图中与∠EOC互余的角有∠COD,∠BOD;
(3)∠COE有补角,
理由:∵ ∠AOE=∠EOC,∠AOE+∠BOE=180?,
∴ ∠COE+∠BOE=180?,
∴ ∠COE有补角是∠BOE.
24.
【解析】
结合∠1=2∠3,利用对顶角相等的性质求出∠3的度数,再求∠4的度数.
【解答】
解:根据对顶角相等,得∠1=∠2=65?,
∵ ∠1=2∠3,
∴ ∠3=32.5?,
∴ ∠4=∠3=32.5?.
25.
【解析】
结合∠1=2∠3,利用对顶角相等的性质求出∠3的度数,再求∠4的度数.
【解答】
解:根据对顶角相等,得∠1=∠2=86?,
∵ ∠1=2∠3,
∴ ∠3=43?,
∴ ∠4=∠3=43?.
26.
【解析】
(1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;
(2)根据(1)中结论即可判定垂直;
(3)根据规律发现,与脚码是偶数的直线互相平行,与脚码是奇数的直线互相垂直,根据此规律即可判断.
【解答】
解:(1)a1⊥a3.
理由如下:如图1,∵ a1⊥a2,
∴ ∠1=90?,
∵ a2?//?a3,
∴ ∠2=∠1=90?,
∴ a1⊥a3;
(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1?//?a4;
(3)直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1?//?a4,
以此类推,直线a1与a2020的位置关系是:a1⊥a2020.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
