人教版 八年级数学上册 12.2 全等三角形的判定 课时训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 12.2 全等三角形的判定 课时训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 399.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-04 11:29:50 | ||
图片预览

文档简介
人教版 八年级数学上册 12.2 全等三角形的判定 课时训练
一、选择题
1. 如图,已知AB=DE,∠B=∠E,为了直接用“ASA”说明△ABC≌△DEF,则需要添加的条件是( )
A.BC=EF B.∠A=∠D
C.∠C=∠F D.AC=DF
2. 如图所示,∠C=∠D=90°,若要用“HL”判定Rt△ABC与Rt△ABD全等,则可添加的条件是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3. 下列三角形中全等的是( )
A.①② B.②③ C.③④ D.①④
4. 如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
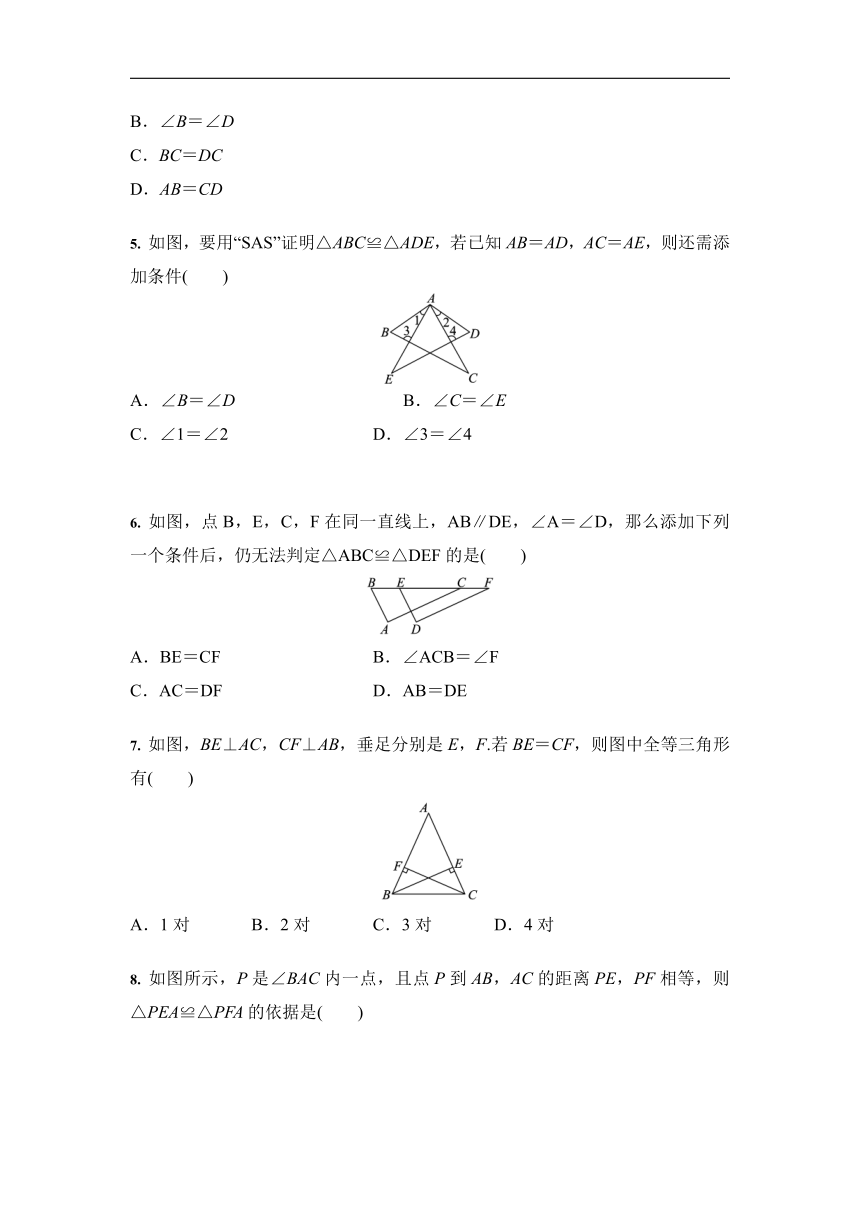
5. 如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D B.∠C=∠E
C.∠1=∠2 D.∠3=∠4
6. 如图,点B,E,C,F在同一直线上,AB∥DE,∠A=∠D,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.BE=CF B.∠ACB=∠F
C.AC=DF D.AB=DE
7. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PFA的依据是( )
A.HL B.ASA C.SSS D.SAS
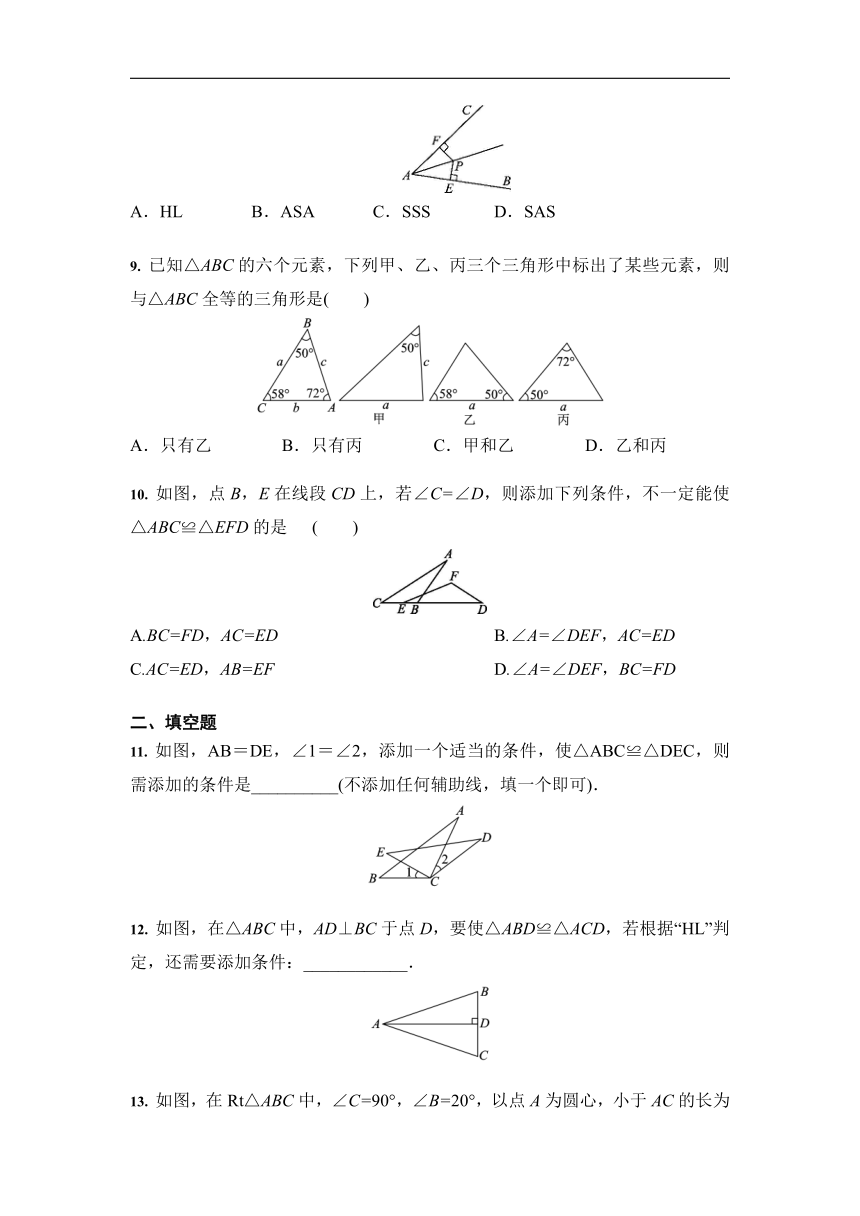
9. 已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
10. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
二、填空题
11. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
12. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.
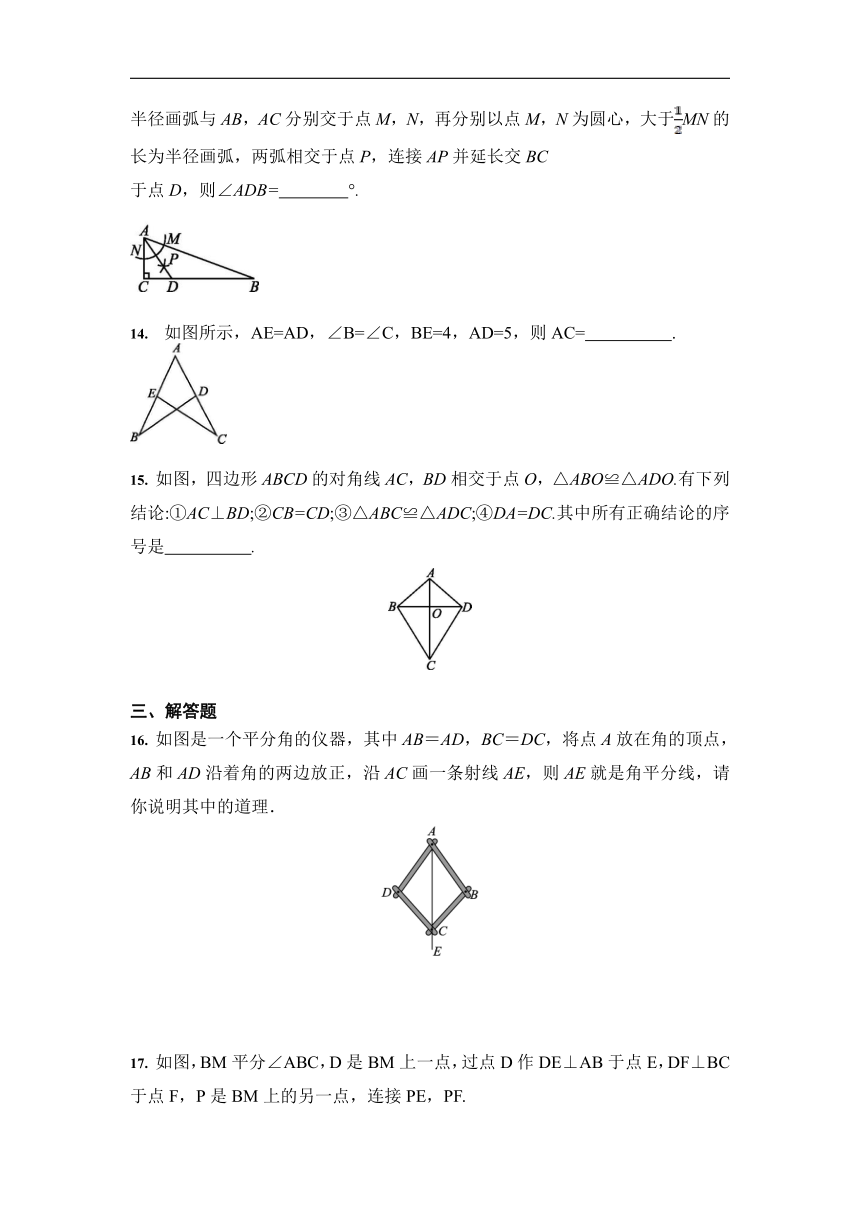
13. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC
于点D,则∠ADB= °.?
14. 如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC= . ?
15. 如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .?
三、解答题
16. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放正,沿AC画一条射线AE,则AE就是角平分线,请你说明其中的道理.
17. 如图,BM平分∠ABC,D是BM上一点,过点D作DE⊥AB于点E,DF⊥BC于点F,P是BM上的另一点,连接PE,PF.
(1)若∠EDF=124°,求∠ABC的度数;
(2)求证:PE=PF.
18. 如图所示,在一条笔直的海岸线上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸线的距离相等吗?为什么?
19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下.
如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC、BD相交于O,OD⊥CD,垂足为D.已知AB=20米,请根据上述信息求标语CD的长度.
人教版 八年级数学上册 12.2 全等三角形的判定 课时训练-答案
一、选择题
1. 【答案】B
2. 【答案】A
3. 【答案】A [解析] ①②符合证明三角形全等的判定方法“SAS”.③④中相等的角所对的边不相等,所以不可能全等.故选A.
4. 【答案】C
5. 【答案】C [解析] 还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
6. 【答案】B
7. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
8. 【答案】A
9. 【答案】D
10. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
二、填空题
11. 【答案】答案不唯一,如∠B=∠E
12. 【答案】AB=AC
13. 【答案】125 [解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.
∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.
14. 【答案】 9
15. 【答案】①②③ [解析] 由△ABO≌△ADO,得AB=AD,∠AOB=∠AOD=90°,∠BAC=∠DAC.
又因为AC=AC,所以△ABC≌△ADC,则CB=CD.所以①②③正确.
三、解答题
16. 【答案】
解:在△ABC与△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC,即AE平分∠BAD.
17. 【答案】
解:(1)∵DE⊥AB,DF⊥BC,
∴∠DEB=∠DFB=90°.
∵∠EDF=124°,
∴∠ABC=360°-90°-90°-124°=56°.
(2)证明:∵BM平分∠ABC,DE⊥AB,DF⊥BC,
∴∠ABM=∠CBM,DE=DF.
∵∠BDE=90°-∠ABM,∠BDF=90°-∠CBM,
∴∠BDE=∠BDF.
∴∠EDP=∠FDP.
在△EDP和△FDP中,
∴△EDP≌△FDP(SAS).∴PE=PF.
18. 【答案】
解:相等.理由:设AD,BC相交于点O.
∵∠CAD=∠CBD,∠COA=∠DOB,
∴由三角形内角和定理,得∠C=∠D.
由已知得∠CAB=∠DBA=90°.
在△CAB和△DBA中,
∴△CAB≌△DBA.
∴CA=DB.
∴海岛C,D到观测点A,B所在海岸线的距离相等.
19. 【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20. 【答案】
解:∵AB∥CD,OD⊥CD,
∴OB⊥AB,
∵相邻两平行线间的距离相等,
∴OB=OD.(3分)
在△ABO与△CDO中,
,
∴△ABO≌△CDO(ASA),(6分)
∴CD=AB=20(米).(7分)
一、选择题
1. 如图,已知AB=DE,∠B=∠E,为了直接用“ASA”说明△ABC≌△DEF,则需要添加的条件是( )
A.BC=EF B.∠A=∠D
C.∠C=∠F D.AC=DF
2. 如图所示,∠C=∠D=90°,若要用“HL”判定Rt△ABC与Rt△ABD全等,则可添加的条件是( )
A.AC=AD B.AB=AB
C.∠ABC=∠ABD D.∠BAC=∠BAD
3. 下列三角形中全等的是( )
A.①② B.②③ C.③④ D.①④
4. 如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
5. 如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D B.∠C=∠E
C.∠1=∠2 D.∠3=∠4
6. 如图,点B,E,C,F在同一直线上,AB∥DE,∠A=∠D,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.BE=CF B.∠ACB=∠F
C.AC=DF D.AB=DE
7. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
8. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PFA的依据是( )
A.HL B.ASA C.SSS D.SAS
9. 已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
10. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
二、填空题
11. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
12. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.
13. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC
于点D,则∠ADB= °.?
14. 如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC= . ?
15. 如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .?
三、解答题
16. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放正,沿AC画一条射线AE,则AE就是角平分线,请你说明其中的道理.
17. 如图,BM平分∠ABC,D是BM上一点,过点D作DE⊥AB于点E,DF⊥BC于点F,P是BM上的另一点,连接PE,PF.
(1)若∠EDF=124°,求∠ABC的度数;
(2)求证:PE=PF.
18. 如图所示,在一条笔直的海岸线上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸线的距离相等吗?为什么?
19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.
(1)若∠ABF=63°,求∠ADE的度数;
(2)若AB=AD,求证:DE=BF+EF.
20. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下.
如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC、BD相交于O,OD⊥CD,垂足为D.已知AB=20米,请根据上述信息求标语CD的长度.
人教版 八年级数学上册 12.2 全等三角形的判定 课时训练-答案
一、选择题
1. 【答案】B
2. 【答案】A
3. 【答案】A [解析] ①②符合证明三角形全等的判定方法“SAS”.③④中相等的角所对的边不相等,所以不可能全等.故选A.
4. 【答案】C
5. 【答案】C [解析] 还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
6. 【答案】B
7. 【答案】C [解析] ①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
8. 【答案】A
9. 【答案】D
10. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
二、填空题
11. 【答案】答案不唯一,如∠B=∠E
12. 【答案】AB=AC
13. 【答案】125 [解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.
∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.
14. 【答案】 9
15. 【答案】①②③ [解析] 由△ABO≌△ADO,得AB=AD,∠AOB=∠AOD=90°,∠BAC=∠DAC.
又因为AC=AC,所以△ABC≌△ADC,则CB=CD.所以①②③正确.
三、解答题
16. 【答案】
解:在△ABC与△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC,即AE平分∠BAD.
17. 【答案】
解:(1)∵DE⊥AB,DF⊥BC,
∴∠DEB=∠DFB=90°.
∵∠EDF=124°,
∴∠ABC=360°-90°-90°-124°=56°.
(2)证明:∵BM平分∠ABC,DE⊥AB,DF⊥BC,
∴∠ABM=∠CBM,DE=DF.
∵∠BDE=90°-∠ABM,∠BDF=90°-∠CBM,
∴∠BDE=∠BDF.
∴∠EDP=∠FDP.
在△EDP和△FDP中,
∴△EDP≌△FDP(SAS).∴PE=PF.
18. 【答案】
解:相等.理由:设AD,BC相交于点O.
∵∠CAD=∠CBD,∠COA=∠DOB,
∴由三角形内角和定理,得∠C=∠D.
由已知得∠CAB=∠DBA=90°.
在△CAB和△DBA中,
∴△CAB≌△DBA.
∴CA=DB.
∴海岛C,D到观测点A,B所在海岸线的距离相等.
19. 【答案】
解:(1)∵AD∥BC,AB⊥BC,
∴∠ABC=∠BAD=90°.
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠AED=90°.
∴∠ABF+∠BAF=∠BAF+∠DAE=90°.
∴∠DAE=∠ABF=63°.∴∠ADE=27°.
(2)证明:由(1)得∠DAE=∠ABF,∠AED=∠BFA=90°.
在△DAE和△ABF中,
∴△DAE≌△ABF(AAS).
∴AE=BF,DE=AF.
∴DE=AF=AE+EF=BF+EF.
20. 【答案】
解:∵AB∥CD,OD⊥CD,
∴OB⊥AB,
∵相邻两平行线间的距离相等,
∴OB=OD.(3分)
在△ABO与△CDO中,
,
∴△ABO≌△CDO(ASA),(6分)
∴CD=AB=20(米).(7分)
