24.2.2 直线和圆的位置关系 第2课时 切线的判定与性质 课件(共24张PPT)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 第2课时 切线的判定与性质 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
24.2.2
直线和圆的位置关系?
第2课时
切线的判定与性质
人教版·九年级数学上册
上课课件
学习目标
1.掌握切线的判定定理,能判定一条直线是否为圆的切线.
2.掌握切线的性质定理.
3.能综合运用圆的切线的判定和性质解决问题.
【学习重点】
探索圆的切线的判定和性质,并能运用.
【学习难点】
探索圆的切线的判定方法.
新课导入
情景1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的?
情景2:砂轮转动时,火星是沿着砂轮的什么方向飞出去的?
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
都是沿切线方向飞出的.
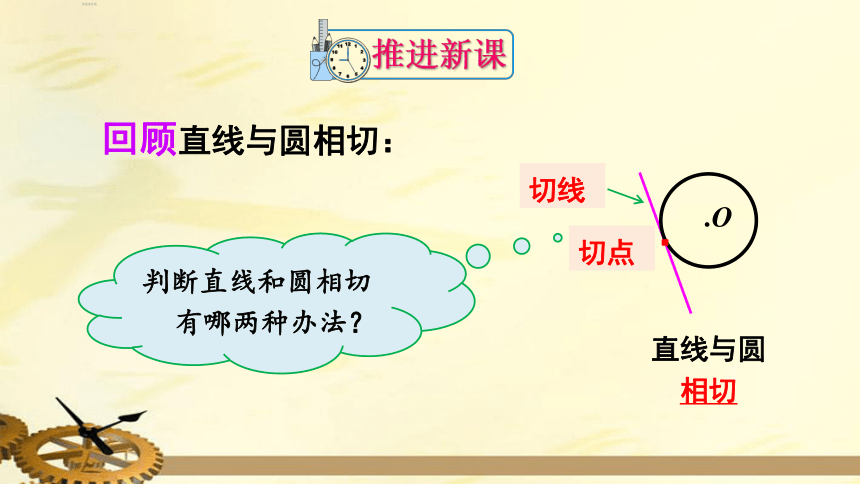
推进新课
回顾直线与圆相切:
.O
直线与圆相切
切线
.
切点
判断直线和圆相切有哪两种办法?
1.
和圆有且只有一个公共点的直线是圆的切线.
2.
圆心到直线的距离等于半径的直线是圆的切线.
1.切线和圆只有一个公共点.
2.圆心到切线的距离等于半径.
切线具有什么性质?
定义法:
数量法(d=r
):
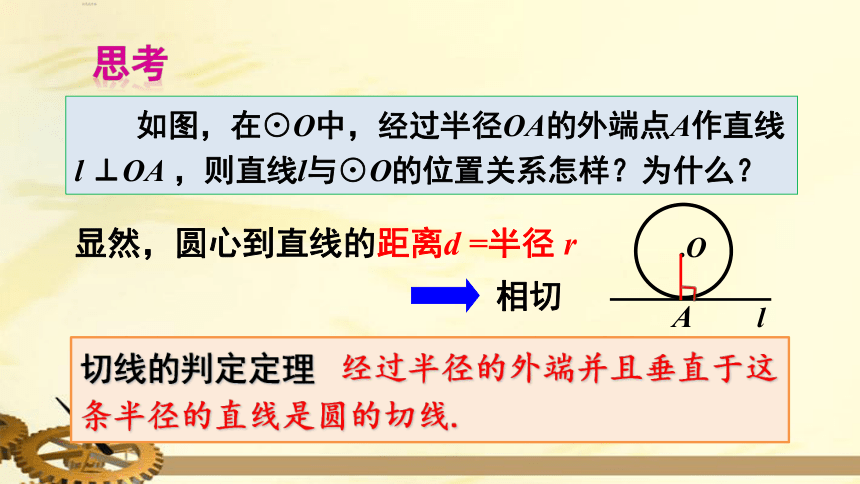
如图,在⊙O中,经过半径OA的外端点A作直线
l
⊥OA
,则直线l与⊙O的位置关系怎样?为什么?
条件一:直线l
经过半径OA的外端点A.
条件二:直线l
垂直于半径OA.
显然,圆心到直线的距离d
=半径
r
相切
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
思考
l
.O
A
∵
OA⊥l
∴
l是⊙O的切线.
几何符号表达:
OA是半径,
于A
l
.O
A
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
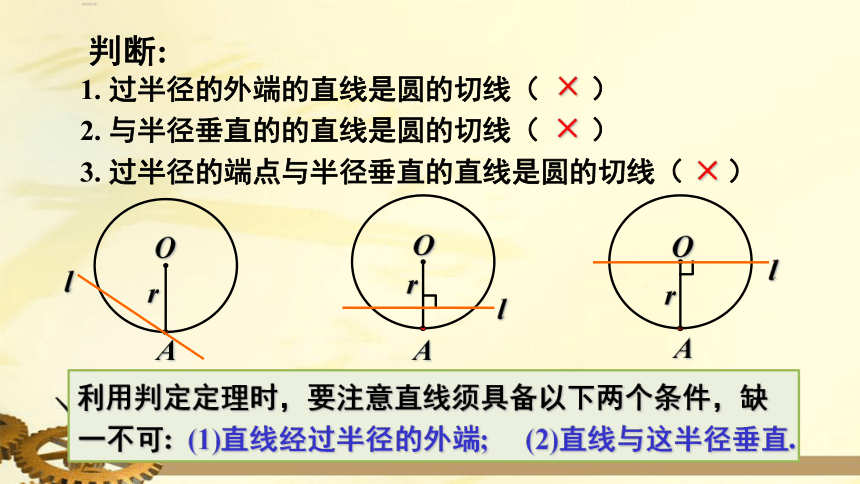
判断:
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
l
.O
.
A
第一步:连接OA;
第二步:过A点作OA的垂线l.
判断一条直线是圆的切线,你现在会哪几种方法?
有以下三种方法
切线的判定方法
1.定义法:和圆有且只有一个公共点的直线是圆的切线.
2.数量法(d=r):圆心到直线的距离等于半径的直线是圆的切线.
3.判定定理:经过半径外端且垂直于这条半径的直线是圆的切线.
归纳
下雨天快速转动雨伞时飞出的水滴,以及在砂轮上打磨工件飞出的火星,均沿着圆的切线的方向飞出.
1.
当你在下雨天快速转动雨伞时,水滴顺着伞的什么方向飞出去的?
2.
砂轮打磨零件时,溅出火星沿着砂轮的什么方向飞出去的?
生活中的数学
改变切线判定定理的题设与结论:
如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?
切线的性质定理:
圆的切线垂直于过切点的半径.
∵直线l切⊙O于点A,
∴OA⊥l
几何符号表达:
l
.O
.
A
反证法
思考
1.圆的切线和圆只有一个公共点.
2.圆心到切线的距离等于半径.
3.圆的切线垂直于过切点的半径.
切线的性质
归纳
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
例1
.
O
A
D
B
C
E
证明:连接OD,作OE⊥AC
于E
.
∴∠OEC=90°.
∵
AB是⊙O的切线,
∴OD⊥AB.
∴∠ODB=90
°
=∠OEC.
∵AB=AC
,∴∠B=∠C.
∵O是BC的中点,
∴OB=OC
.
∴△OBD≌△OCE(AAS),
∴OD=OE
.
∴AC与⊙O相切.
随堂演练
基础巩固
1.下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线
B.到圆心的距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径的外端的直线是圆的切线
B
2.如图,已知⊙O的直径AB与弦AC的
夹角为31°,过C点的切线PC与AB的
延长线交于点P,则∠P等于(
)
A.24°
B.25°
C.28°
D.30°
3.如图,AB与⊙O切于点C,OA=OB,
若⊙O的半径为8cm,AB=10cm,则
OA的长为
cm.
C
4.如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,求证:AP=BP.
证明:连接OP.
∵AB切⊙O于点P,
∴OP⊥AB.
∴AP=BP(垂径定理).
5.如图,AB是⊙O的直径,∠B=∠CAD.求证:AC是⊙O的切线.
证明:∵AB是⊙O的直径,
∴∠BDA=90°.
∴∠B+∠BAD=90°.
又∵∠B=∠CAD.
∴∠CAD+∠BAD=∠BAC=90°.
∵AC过点A,∴AC是⊙O的切线.
6.如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE是⊙O的切线,交AC的延长线于点E.
求证:DE⊥AC.
证明:连接OD.∵AD是∠BAC的平分线,
∴∠EAD=∠DAO.又∵OA=OD.
∴∠DAO=∠ODA.
∴∠ODA=∠EAD.∴OD∥AC.
又∵DE是⊙O的切线,
∴∠ODE=90°.∴∠E=90°.即DE⊥AC.
综合应用
7.如图,利用刻度尺和三角尺可以测量圆形工件的直径,说明其中的道理.
解:因为两个三角尺的一条直角边与圆相切,另一条直角边在一条直线上,所以两条切线互相平行.
则连接两切点之间的线段就是圆的
直径,利用图中刻度尺就可以测量
出图形工件的直径.
拓展延伸
课堂小结
切线的性质定理:
圆的切线垂直于过切点的半径.
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
24.2.2
直线和圆的位置关系?
第2课时
切线的判定与性质
人教版·九年级数学上册
上课课件
学习目标
1.掌握切线的判定定理,能判定一条直线是否为圆的切线.
2.掌握切线的性质定理.
3.能综合运用圆的切线的判定和性质解决问题.
【学习重点】
探索圆的切线的判定和性质,并能运用.
【学习难点】
探索圆的切线的判定方法.
新课导入
情景1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的?
情景2:砂轮转动时,火星是沿着砂轮的什么方向飞出去的?
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
都是沿切线方向飞出的.
推进新课
回顾直线与圆相切:
.O
直线与圆相切
切线
.
切点
判断直线和圆相切有哪两种办法?
1.
和圆有且只有一个公共点的直线是圆的切线.
2.
圆心到直线的距离等于半径的直线是圆的切线.
1.切线和圆只有一个公共点.
2.圆心到切线的距离等于半径.
切线具有什么性质?
定义法:
数量法(d=r
):
如图,在⊙O中,经过半径OA的外端点A作直线
l
⊥OA
,则直线l与⊙O的位置关系怎样?为什么?
条件一:直线l
经过半径OA的外端点A.
条件二:直线l
垂直于半径OA.
显然,圆心到直线的距离d
=半径
r
相切
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
思考
l
.O
A
∵
OA⊥l
∴
l是⊙O的切线.
几何符号表达:
OA是半径,
于A
l
.O
A
切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
判断:
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
l
.O
.
A
第一步:连接OA;
第二步:过A点作OA的垂线l.
判断一条直线是圆的切线,你现在会哪几种方法?
有以下三种方法
切线的判定方法
1.定义法:和圆有且只有一个公共点的直线是圆的切线.
2.数量法(d=r):圆心到直线的距离等于半径的直线是圆的切线.
3.判定定理:经过半径外端且垂直于这条半径的直线是圆的切线.
归纳
下雨天快速转动雨伞时飞出的水滴,以及在砂轮上打磨工件飞出的火星,均沿着圆的切线的方向飞出.
1.
当你在下雨天快速转动雨伞时,水滴顺着伞的什么方向飞出去的?
2.
砂轮打磨零件时,溅出火星沿着砂轮的什么方向飞出去的?
生活中的数学
改变切线判定定理的题设与结论:
如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?
切线的性质定理:
圆的切线垂直于过切点的半径.
∵直线l切⊙O于点A,
∴OA⊥l
几何符号表达:
l
.O
.
A
反证法
思考
1.圆的切线和圆只有一个公共点.
2.圆心到切线的距离等于半径.
3.圆的切线垂直于过切点的半径.
切线的性质
归纳
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
例1
.
O
A
D
B
C
E
证明:连接OD,作OE⊥AC
于E
.
∴∠OEC=90°.
∵
AB是⊙O的切线,
∴OD⊥AB.
∴∠ODB=90
°
=∠OEC.
∵AB=AC
,∴∠B=∠C.
∵O是BC的中点,
∴OB=OC
.
∴△OBD≌△OCE(AAS),
∴OD=OE
.
∴AC与⊙O相切.
随堂演练
基础巩固
1.下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线
B.到圆心的距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线
D.过圆的半径的外端的直线是圆的切线
B
2.如图,已知⊙O的直径AB与弦AC的
夹角为31°,过C点的切线PC与AB的
延长线交于点P,则∠P等于(
)
A.24°
B.25°
C.28°
D.30°
3.如图,AB与⊙O切于点C,OA=OB,
若⊙O的半径为8cm,AB=10cm,则
OA的长为
cm.
C
4.如图,以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,求证:AP=BP.
证明:连接OP.
∵AB切⊙O于点P,
∴OP⊥AB.
∴AP=BP(垂径定理).
5.如图,AB是⊙O的直径,∠B=∠CAD.求证:AC是⊙O的切线.
证明:∵AB是⊙O的直径,
∴∠BDA=90°.
∴∠B+∠BAD=90°.
又∵∠B=∠CAD.
∴∠CAD+∠BAD=∠BAC=90°.
∵AC过点A,∴AC是⊙O的切线.
6.如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE是⊙O的切线,交AC的延长线于点E.
求证:DE⊥AC.
证明:连接OD.∵AD是∠BAC的平分线,
∴∠EAD=∠DAO.又∵OA=OD.
∴∠DAO=∠ODA.
∴∠ODA=∠EAD.∴OD∥AC.
又∵DE是⊙O的切线,
∴∠ODE=90°.∴∠E=90°.即DE⊥AC.
综合应用
7.如图,利用刻度尺和三角尺可以测量圆形工件的直径,说明其中的道理.
解:因为两个三角尺的一条直角边与圆相切,另一条直角边在一条直线上,所以两条切线互相平行.
则连接两切点之间的线段就是圆的
直径,利用图中刻度尺就可以测量
出图形工件的直径.
拓展延伸
课堂小结
切线的性质定理:
圆的切线垂直于过切点的半径.
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
同课章节目录
