24.2.2 直线和圆的位置关系 第1课时 直线和圆的位置关系 课件(共24张PPT)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 第1课时 直线和圆的位置关系 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 892.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 19:47:20 | ||
图片预览





文档简介
(共24张PPT)
24.2.2
直线和圆的位置关系
第1课时
直线和圆的位置关系
人教版·九年级数学上册
上课课件
学习目标
1.通过操作、观察,理解直线和圆有三种位置关系.
2.根据圆心到直线的距离与半径之间的数量关系判定直线和圆的位置关系.
3.经历探索直线和圆的位置关系的判定和专题训练,体验从运动观点以及量变到质变的过程理解直线和圆三种位置关系.
【学习重点】
直线和圆的位置关系的判定.
【学习难点】
直线和圆的位置关系的判定.
新课导入
情景:如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
问题:直线和圆有几种位置关系?怎样判断直线和圆的位置关系?
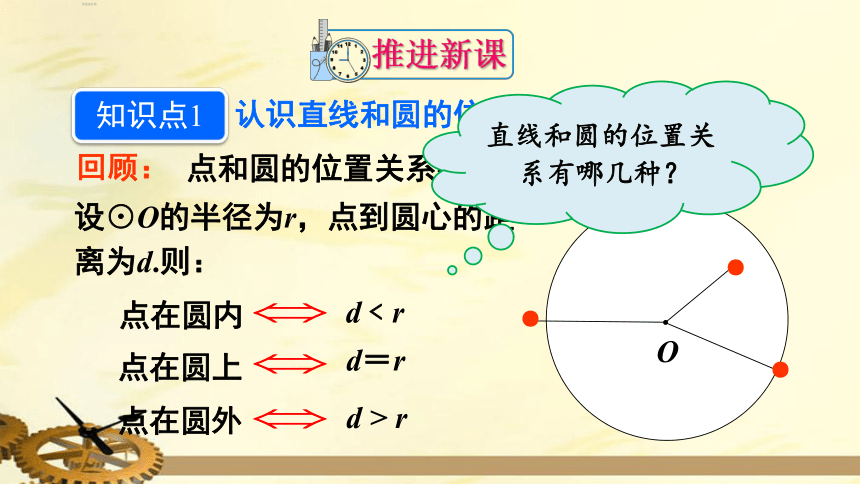
认识直线和圆的位置关系
点和圆的位置关系有哪几种?
回顾:
设⊙O的半径为r,点到圆心的距离为d.则:
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d
>
r
●
●
●
.
O
推进新课
直线和圆的位置关系有哪几种?
知识点1
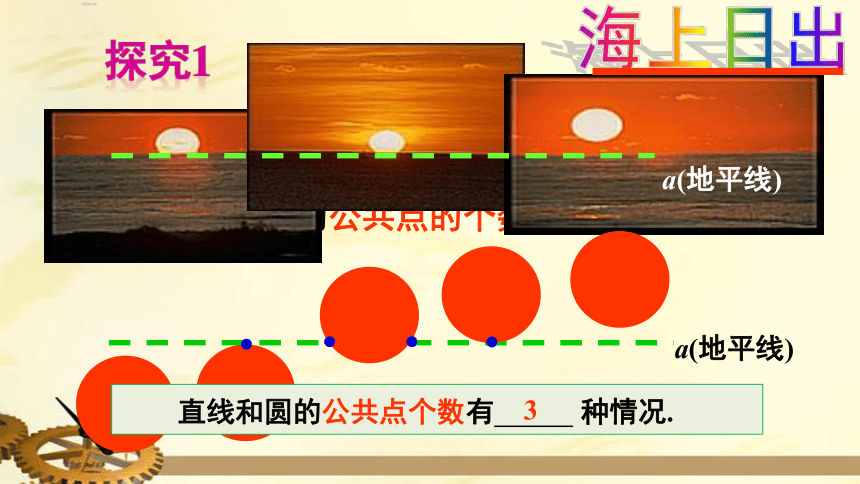
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
直线和圆的公共点个数有
种情况.
海上日出
●
●
●
●
探究1
3
●
●
●
●
按直线与圆的公共点的个数可分为:
个公共点
0
个公共点
1
个公共点
2
直线与圆的位置关系
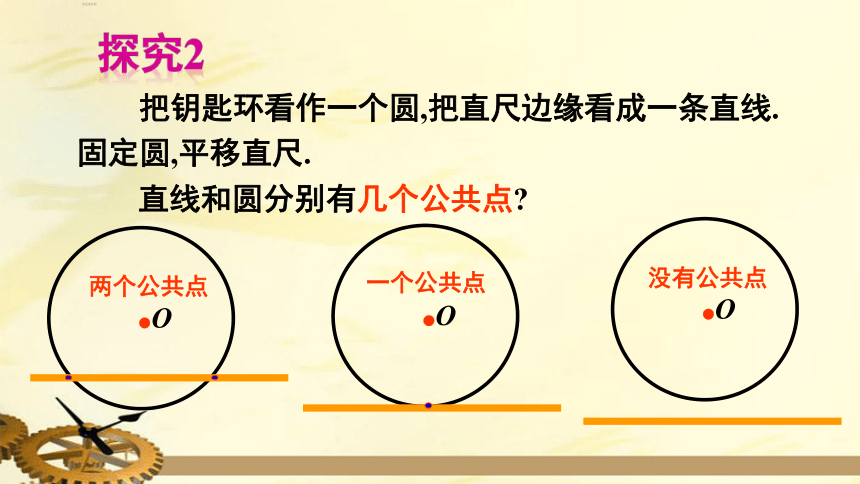
探究2
把钥匙环看作一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺.
直线和圆分别有几个公共点?
●O
●O
●O
两个公共点
没有公共点
一个公共点
0个公共点
.O
1个公共点
.O
2个公共点
.O
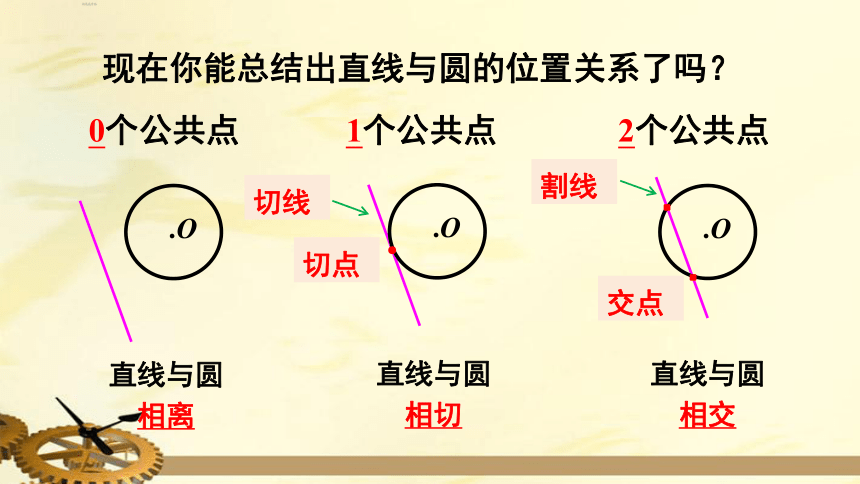
直线与圆相离
直线与圆相切
直线与圆相交
切线
.
切点
割线
现在你能总结出直线与圆的位置关系了吗?
.
.
交点
已知,直线与圆的位置关系有
种,分别是
、
、
.
判断直线和圆的位置关系
知识点2
3
相离
相切
相交
怎么判断直线和圆的位置关系呢?
快速判断下列各图中直线与圆的位置关系.
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1
.
直线l与
O2
.
O
●
●
●
●
●
相离
相交
从直线与圆公共点的个数可以判断出直线与圆的位置关系.
方法一:
还可以怎么判断直线和圆的位置关系?
过直线外一点作这条直线的垂线段,
垂线段的长度叫点到直线的距离.
l
.O
D
如图,设⊙O的半径为r,圆心O到直线l的距离为d.则d与⊙O的半径r的大小有什么关系?
.O
.O
r
d
r
d
相离
相切
d
r
<
d
r
=
你能根据d与r的大小关系确定直线与圆的位置关系吗?
.O
r
d
相交
d
r
>
设⊙O的半径为r,圆心到直线的距离为d.则
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d
>
r
.
O
l1
l2
l3
d
d
d
r
方法二:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)由
大小关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳
随堂演练
基础巩固
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是(
)
A.相离
B.相切
C.相交
D.无法判断
2.直线l与半径为r的⊙O相离,且点O到直线l的距离为6,则r的取值范围是(
)
A.r<6
B.r=6
C.r>6
D.r≥6
C
A
3.⊙O的半径为4cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系为
.
?
4.如图,在Rt△ABC中,∠C=90°,
∠A=60°,BC=4cm,以点C为圆心,
3cm长为半径作圆,则⊙C与AB的
位置关系是
.
?
相切
相交
5.如图,已知∠AOB=30°,M为OB边上一点,OM=5cm,以点M为圆心,r为半径的⊙M与直线OA有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
?
解:过M作MN⊥OA,垂足为N.
∵∠AOB=30°,∠MNO=90°,
∴MN=
OM=2.5cm.
所以(1)⊙M与直线OA相离,因为r(2)⊙M与直线OA相交,因为r>MN.
(3)⊙M与直线OA相切,因为r=MN.
6.已知⊙O的半径为
,直线l与点O的距离为d,若直线l与⊙O有公共点,则(
)
A.d﹥
B.d=
C.d﹤
D.d≤
?
7.直线l
和⊙O有公共点,则直线l与⊙O(
)
A.相离
B.相切
C.相交
D.相切或相交
?
综合应用
D
D
8.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为
.
解析:若与OA,AB,BC三条边相切,D的坐
标为(3,1);若与OA,BC,CO三条边相切,
D的坐标为(1,1);若与OA,AB,CO三条边
相切,D的坐标为(2,2);若与AB,BC,CO三
条边相切,D的坐标为(2,0).
?
拓展延伸
(1,1),(3,1)(2,2)和(2,0)
课堂小结
直线与圆的位置关系
相离
相切
相交
大致图象
数量关系(d、r)
交点个数
0
1
2
d﹤r
d=r
d
>
r
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
24.2.2
直线和圆的位置关系
第1课时
直线和圆的位置关系
人教版·九年级数学上册
上课课件
学习目标
1.通过操作、观察,理解直线和圆有三种位置关系.
2.根据圆心到直线的距离与半径之间的数量关系判定直线和圆的位置关系.
3.经历探索直线和圆的位置关系的判定和专题训练,体验从运动观点以及量变到质变的过程理解直线和圆三种位置关系.
【学习重点】
直线和圆的位置关系的判定.
【学习难点】
直线和圆的位置关系的判定.
新课导入
情景:如图,在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
问题:直线和圆有几种位置关系?怎样判断直线和圆的位置关系?
认识直线和圆的位置关系
点和圆的位置关系有哪几种?
回顾:
设⊙O的半径为r,点到圆心的距离为d.则:
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d
>
r
●
●
●
.
O
推进新课
直线和圆的位置关系有哪几种?
知识点1
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数.
a(地平线)
a(地平线)
直线和圆的公共点个数有
种情况.
海上日出
●
●
●
●
探究1
3
●
●
●
●
按直线与圆的公共点的个数可分为:
个公共点
0
个公共点
1
个公共点
2
直线与圆的位置关系
探究2
把钥匙环看作一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺.
直线和圆分别有几个公共点?
●O
●O
●O
两个公共点
没有公共点
一个公共点
0个公共点
.O
1个公共点
.O
2个公共点
.O
直线与圆相离
直线与圆相切
直线与圆相交
切线
.
切点
割线
现在你能总结出直线与圆的位置关系了吗?
.
.
交点
已知,直线与圆的位置关系有
种,分别是
、
、
.
判断直线和圆的位置关系
知识点2
3
相离
相切
相交
怎么判断直线和圆的位置关系呢?
快速判断下列各图中直线与圆的位置关系.
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1
.
直线l与
O2
.
O
●
●
●
●
●
相离
相交
从直线与圆公共点的个数可以判断出直线与圆的位置关系.
方法一:
还可以怎么判断直线和圆的位置关系?
过直线外一点作这条直线的垂线段,
垂线段的长度叫点到直线的距离.
l
.O
D
如图,设⊙O的半径为r,圆心O到直线l的距离为d.则d与⊙O的半径r的大小有什么关系?
.O
.O
r
d
r
d
相离
相切
d
r
<
d
r
=
你能根据d与r的大小关系确定直线与圆的位置关系吗?
.O
r
d
相交
d
r
>
设⊙O的半径为r,圆心到直线的距离为d.则
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d
>
r
.
O
l1
l2
l3
d
d
d
r
方法二:
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)由
大小关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳
随堂演练
基础巩固
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是(
)
A.相离
B.相切
C.相交
D.无法判断
2.直线l与半径为r的⊙O相离,且点O到直线l的距离为6,则r的取值范围是(
)
A.r<6
B.r=6
C.r>6
D.r≥6
C
A
3.⊙O的半径为4cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系为
.
?
4.如图,在Rt△ABC中,∠C=90°,
∠A=60°,BC=4cm,以点C为圆心,
3cm长为半径作圆,则⊙C与AB的
位置关系是
.
?
相切
相交
5.如图,已知∠AOB=30°,M为OB边上一点,OM=5cm,以点M为圆心,r为半径的⊙M与直线OA有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=4cm;
(3)r=2.5cm.
?
解:过M作MN⊥OA,垂足为N.
∵∠AOB=30°,∠MNO=90°,
∴MN=
OM=2.5cm.
所以(1)⊙M与直线OA相离,因为r
(3)⊙M与直线OA相切,因为r=MN.
6.已知⊙O的半径为
,直线l与点O的距离为d,若直线l与⊙O有公共点,则(
)
A.d﹥
B.d=
C.d﹤
D.d≤
?
7.直线l
和⊙O有公共点,则直线l与⊙O(
)
A.相离
B.相切
C.相交
D.相切或相交
?
综合应用
D
D
8.如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为
.
解析:若与OA,AB,BC三条边相切,D的坐
标为(3,1);若与OA,BC,CO三条边相切,
D的坐标为(1,1);若与OA,AB,CO三条边
相切,D的坐标为(2,2);若与AB,BC,CO三
条边相切,D的坐标为(2,0).
?
拓展延伸
(1,1),(3,1)(2,2)和(2,0)
课堂小结
直线与圆的位置关系
相离
相切
相交
大致图象
数量关系(d、r)
交点个数
0
1
2
d﹤r
d=r
d
>
r
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
同课章节目录
