24.1.1 圆 课件（共22张PPT）

(共22张PPT)
人教版·九年级数学上册
上课课件
24.1
圆的有关性质
24.1.1
圆
【学习目标】
1．理解圆、弧、等弧、弦、等圆、半圆、直径等有关概念．
2．能初步应用“同圆的半径相等”及“圆心是任一直径的中点”进行简单的证明和计算．
【学习重点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的理解．
【学习难点】
圆、等圆、弧、等弧、弦、半圆、直径等有关概念的区别与联系．
新课导入
这些图片中都有哪种图形？
圆
看了此画,你有何想法?
思考：车轮为什么做成圆形?做成三角形、正方形可以吗？
推进新课
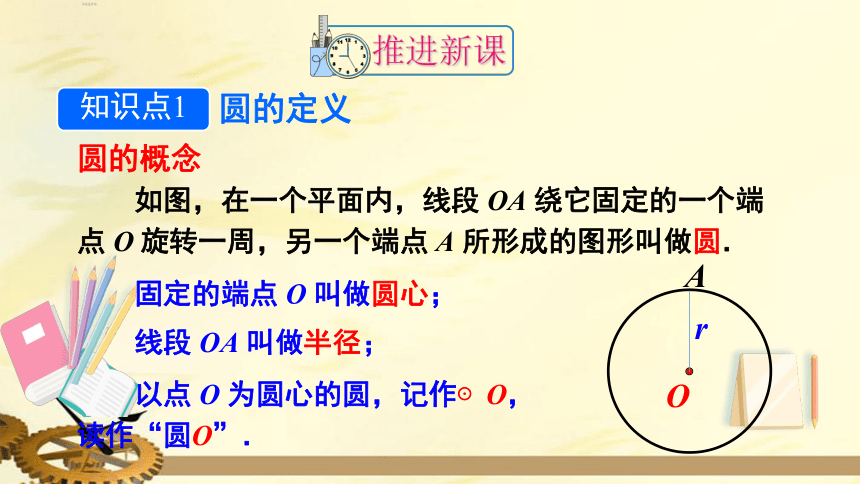
　　如图，在一个平面内，线段
OA
绕它固定的一个端点
O
旋转一周，另一个端点
A
所形成的图形叫做圆．
·
r
O
A
　　固定的端点
O
叫做圆心；
　　线段
OA
叫做半径；
　　以点
O
为圆心的圆，记作⊙O，读作“圆O”．
圆的概念
知识点1
圆的定义
同心圆
等圆
圆心相同，半径不同
　　确定一个圆的两个要素:
　　一是圆心，
二是半径．
半径相同，圆心不同
O
　　问题1：圆上各点到定点（圆心
O）的距离有什么规律？
　　问题2：到定点的距离等于定长的点又有什么特点？
·
r
O
A
　　形成性定义(动态)：在一个平面内，线段
OA
绕它固定的一个端点
O
旋转一周，另一个端点
A
所形成的图形叫做圆．
　　集合性定义(静态)：圆心为
O、半径为
r
的圆可以看成是所有到定点
O
的距离等于定长
r
的点的集合．
战国时的《墨经》
就有“圆,一中同长也”
的记载.它的意思是圆
上各点到圆心的距离都
等于半径.
　　经过圆心的弦叫做直径，如图中的
AB．
　　连接圆上任意两点的线段叫做弦，如图中的
AC．
弦和直径的定义
C
O
A
B
半径是弦吗？
知识点2
与圆有关的概念
　　圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
C
O
A
B
　　弧
　　圆上任意两点间的部分叫做圆弧，简称弧．以
A、B
为端点的弧记作AB，读作“圆弧
AB”或“弧
AB”．
　　劣弧与优弧
　　小于半圆的弧(如图中的
　)叫做劣弧．
AC
　　大于半圆的弧(用三个字母表示，如图中的　　
)叫做优弧．
ABC
C
O
A
B
　　在同圆或等圆
中，能重合的弧
叫等弧．
例1
矩形ABCD的对角线AC,BD相交于点O.求证：A、B、C、D四个点在以点O为圆心的圆上.
典例解析
证明：∵四边形ABCD为矩形，
∴OA=OC=
AC,OB=OD=
BD.
又∵AC=BD，
∴OA=OC=OB=OD.
∴A、B、C、D四个点在以点O为圆心，OA为半径的圆上.
随堂演练
基础巩固
1.下列说法正确的是(
)
A.直径是弦，弦是直径
B.半圆是弧，弧是半圆
C.弦是圆上两点之间的部分
D.半径不是弦，直径是最长的弦
D
2.下列说法中，不正确的是(
)
A.过圆心的弦是圆的直径
B.等弧的长度一定相等
C.周长相等的两个圆是等圆
D.长度相等的两条弧是等弧
D
3.一个圆的最大弦长是10cm，则此圆的半径是
cm.
4.在同一平面内与已知点A的距离等于5cm的所有点所组成的图形是
.
5.如右图，以AB为直径的半圆O上有两点D、E，ED与BA的延长线相交于点C，且有DC=OE，若∠C=20°，则∠EOB的度数是
.
5
圆
60°
6.已知：如图，在⊙O中，AB为弦，C、D两点在AB上，且AC=BD．
求证：OC=OD．
证明：∵OA、OB为⊙O的半径，
∴OA=OB.
∴∠A=∠B.
又∵AC=BD，
∴△ACO≌△BDO.
∴OC=OD.
7.已知：如图，在△ABC中，∠C=90°，求证：A、B、C三点在同一个圆上.
证明：作AB的中点O，连接OC.
∵△ABC是直角三角形.
∴OA=OB=OC=
AB.
∴A、B、C三点在同一个圆上.
综合应用
8.求证：直径是圆中最长的弦.
证明：如图，在⊙O中，AB是⊙O的直径，半径是r.
CD是不同于AB的任意一条弦.
连接OC、OD，
则OA+OB=OC+OD=2r,即AB=OC+OD.
在△OCD中，OC+OD＞CD，
∴AB＞CD.即直径是圆中最长的弦.
拓展延伸
课堂小结
圆的基本概念
圆的定义
与圆有关的概念
形成性定义：
集合性定义：
弦：
直径：
圆弧（弧）：
半圆：
等圆、等弧：
优弧、劣弧：
在一个平面内，线段OA绕它固定的一个端点O旋
转一周，另一个端点A所形成的图形叫做圆.
圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等定长r的点的集合.
连接圆上任意两点的线段叫做弦.
直径是经过圆心的弦，是圆中最长的弦.
圆上任意两点间的部分叫做圆弧，简称弧.
圆的任意一条直径的两个端点把圆分成两条弧，每条弧
都叫做半圆.
能够重合的两个圆叫做等圆，在同圆或等圆中，
能够互相重合的弧叫做等弧.
大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧.
课后作业
1.从课后习题中选取；
2.完成练习册本课时的习题.
谢谢欣赏