关于原点对称的点的坐标

(共19张PPT)
侏儒中学涂厚红
教学目标
1正确认识关于原点对称的两点的坐标间的关系
2能运用关于原点成中心对称的点的坐标间的关系进行中心对称图形的变换
3通过观察、实际操作，理解关于原点对称的点的特征，了解坐标系内中心对称作图的步骤及关键
4结合点的坐标对称关系的学习，培养学生合作学习的意思和善于归纳类比的学习精神
教学重点与难点
教学重点：关于原点对称的点的坐标特征
教学难点：关于坐标系内点对称的点的坐标的探索
☆知识巩固
2、中心对称有何性质？
1、什么叫中心对称和中心对称图形？
☆知识巩固
2、中心对称有何性质？
1、什么叫中心对称和中心对称图形？
一个图形绕某点旋转180度和另一个图形重合。
一个图形绕某点旋转180度和原图形（自身）重合。
（2）关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。
（1）关于中心对称图形的两个图形是全等形。
☆知识巩固
2、中心对称有何性质？
1、什么叫中心对称和中心对称图形？
一个图形绕某点旋转180度和另一个图形重合。
一个图形绕某点旋转180度和原图形（自身）重合。
（2）关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。
（1）关于中心对称图形的两个图形是全等形。
☆知识巩固
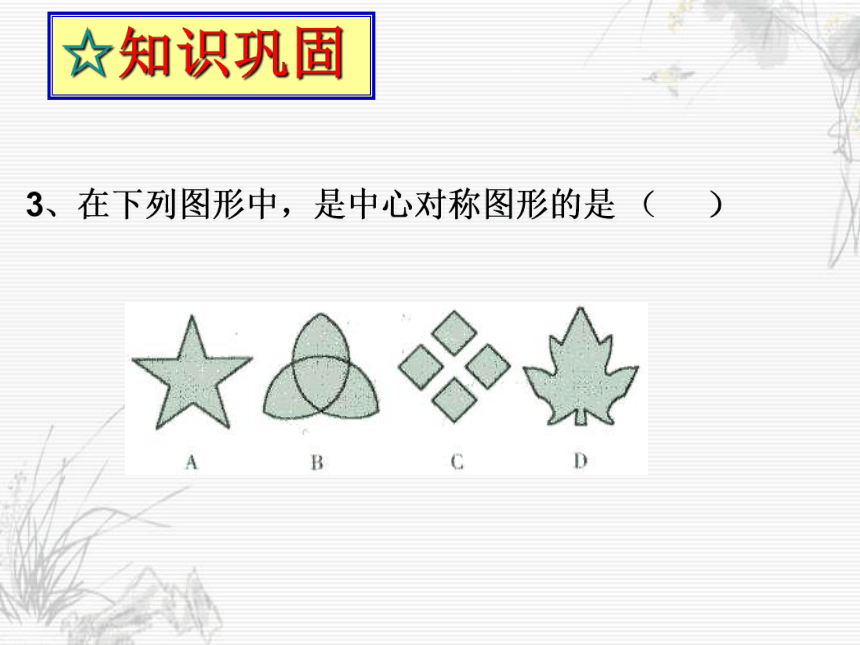
3、在下列图形中，是中心对称图形的是 （ ）
☆知识巩固
3、在下列图形中，是中心对称图形的是 （ ）
C
4、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
5、画出△ABC关于点O的中心对称图形．
4、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是( )
C
A.1个 B.2个 C.3个 D.4个
5、画出△ABC关于点O的中心对称图形．
4、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是( )
C
A.1个 B.2个 C.3个 D.4个
5、画出△ABC关于点O的中心对称图形．
☆探究
如图，在直角坐标系中，已知A（4,0）、B（0,-3）、C（2,1）、D（-1,2）、E（-3,-4），作出A、B、C、D、E点关于原点O的中心对称点，并写出它们的坐标，并回答：这些坐标与已知点的坐标有什么关系？
☆归纳
☆归纳
两个点关于原点对称时，它们的坐标符号相反，
即点P（x,y）关于原点O的对称点P/（-x,-y）．
如图，利用关于原点对称的点的坐标的特点，作出与线段AB关于原点对称的图形．
☆例题精析
1．下列函数中，图象一定关于原点对称的图象是（ ）
A．y= B．y=2x+1
C．y=-2x+1 D．以上三种都不可能
2．如果点P（-3，1），那么点P（-3，1）关于原点
的对称点P/的坐标是P/_______．
3．写出函数y=- 与y= 具有的一个共同
性质________（用对称的观点写）．
☆练一练
4.教材P67 练习．
☆应用拓展
如图，直线AB与x轴、y轴分别相交于A、B两点，将直线AB绕点O顺时针旋转90°得到直线A1B1．
（1）在图中画出直线A1B1．
（2）求出线段A1B1中点的反比例函数解析式．
（3）是否存在另一条与直线AB平行的直线y=kx+b，它与双曲线只有一个交点，若存在，求此直线的函数解析式，若不存在，请说明理由．
如图，直线a⊥b，垂足为O，点A与点A′关于直线a对称，点A′与点A″关于直线b对称，点A与点A″有怎样的对称关系？
你能说明理由吗？
b
a
A''
A'
A
O
☆想一想
小结
本节课你学会了什么